Pymoo:遗传算法原理简介及Pymoo中遗传算子的实现示例
Pymoo:遗传算法原理简介及Pymoo中遗传算子的实现示例
-
-
- 一、遗传算法原理简介
- 二、Pymoo中的遗传算子(Genetic Operators)及其实现
-
- 2.1 抽样算子(Sampling Operator)
- 2.2 选择算子(Selection Operator)
- 2.3 交叉算子(Crossover Operator)
- 2.4 突变算子(Mutation Operator)
-
- Github 仓库: Pymoo: 基于 Python 的多目标优化仓库 (MOO, Multi-objective Optimization)。
- Pymoo文档首页:Multi-objective Optimization in Python
✨ 注意:本文使用Pymoo版本为0.6.0。
一、遗传算法原理简介
遗传算法是一种通过模拟自然进化搜索最优的方法,其主要特点主要体现在以下三个方面:
- 它能直接对结构对象进行操作,不存在求导与函数连续性的限制;
- 具有内在的隐并行性和更好的全局寻优能力;
- 采用概率化的寻优方法,能够自动地获得与指导优化的搜索空间,并能够自适应地调整搜索方向。
具体的流程图如下所示:

在理解遗传算法之前我们需要了解相关的名词如下表所示:
| 名词 | 描述 |
|---|---|
| 基因(gene) | 一个基因代表具体问题的一个决策变量,即自变量 |
| 基因型(genotype) | 性状染色体的内部表现,比如,二进制编码 |
| 表现型(phenotype) | 染色体决定的性状的外部表现,即根据基因型形成的个体外部表现,比如,十进制值 |
| 染色体(chromosome) | 在遗传算法中,问题的每个有效解被成为一个染色体,染色体的具体形式是一个使用特定编码发生生成的编码串,其中每个编码单元称为基因 |
| 个体(individual) | 染色体带有特征的实体,一个包含若干基因的染色体表示一个具体问题的一个解,个体包括染色体与适应度 |
| 种群(population) | 多个个体(染色体)构成一个种群,即一个问题的多组解构成了解的种群 |
| 遗传代数(generation) | 遗传代数,也可以理解为迭代的次数 |
| 适应度(fitness) | 衡量某个物种对于生存环境的适应程度,适应度就是确定自变量后对应的函数值 |
| 编码(coding) | DNA中遗传信息在一个长链上按一定的模式排列,遗传编码可看作从表现型到基因型的映射 |
| 解码(decoding) | 与编码相反,解码为基因型到表现型的映射 |
| 进化(evolution) | 种群逐渐适应生存环境,品质不断得到改良,生物的进化是以种群的形式进行的 |
| 选择(selection) | 以一定的概率从种群中选择若干个个体,通常情况下,选择过程是一种基于适应度的优胜略汰的过程 |
| 复制(reproduction) | 细胞分裂时,遗传物质DNA通过复制而转移到新产色和那个的细胞中,心细胞就继承了旧细胞的基因 |
| 交叉(crossover) | 两个染色体的某一相同位置处DNA被切断,前后两串分别交叉组合形成两个新的染色体,即基因重组或杂交 |
| 变异(mutation) | 在复制的过程中有很小概率产色和那个某些差错,产生新的染色体,表现出新的性状 |
说明:
(1)染色体作为遗传物质的主要载体,即多个基因的组合,其内部表现(基因型)是某种基因组合,它决定了个体的形状的外部表现。因此,在一开始时需要实现编码,即从表现型到基因型的映射实现。为了达到简化的目的,在遗传算法中通常采用二进制编码替代复杂的实际基因编码过程。
(2)遗传算法是从代表问题一个种群(population)开始的,一个种群则经过基因(gene)编码的一定数目的个体(individual)组成的,每个个体实际上是染色体(chromosome)带有特征的实体。
(3)产生初始种群后,逐代(generation)演化出更好的近似解。在每一代中,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)与变异(mutation),产生出代表新解集的种群。
(4)这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。
二、Pymoo中的遗传算子(Genetic Operators)及其实现
Pymoo中的遗传算子包括:抽样算子、选择算子、变异算子与交叉算子。
2.1 抽样算子(Sampling Operator)
在遗传算法开始阶段,初始采样点必须进行抽样。Pymoo提供了Random Sampling与Latin Hypercube Sampling两种方式:
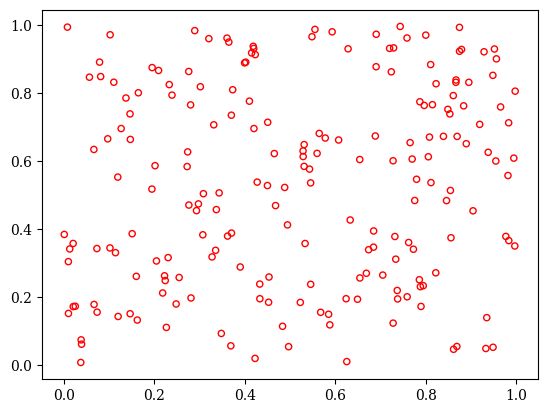
- 1、Random Sampling抽样算子
Random Sampling方法的Pymoo实现代码:
from pymoo.core.problem import Problem
from pymoo.operators.sampling.rnd import FloatRandomSampling
from pymoo.util import plotting
# 构造一个包含两个变量,变量的区间为[0, 1]的问题
problem = Problem(n_var=2, xl=0, xu=1)
# 设置Random Sampling算子
sampling = FloatRandomSampling()
# 从问题problem中随机抽取200个个体
X = sampling(problem, 200).get("X")
# 绘制结果
plotting.plot(X, no_fill=True)
代码执行结果如下图所示:
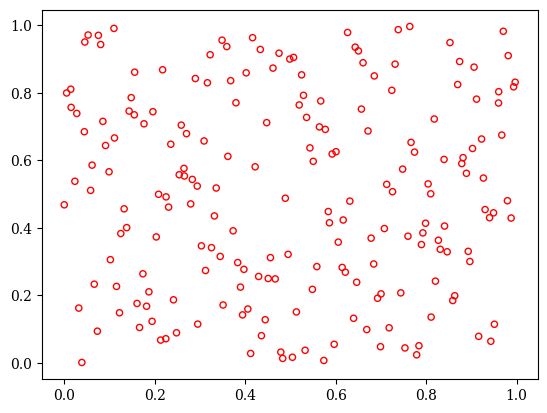
- 2、Latin Hypercube Sampling抽样算子
Latin Hypercube Sampling方法的Pymoo实现代码:
from pymoo.core.problem import Problem
from pymoo.operators.sampling.lhs import LHS
from pymoo.util import plotting
# 构造一个包含两个变量,变量的区间为[0, 1]的问题
problem = Problem(n_var=2, xl=0, xu=1)
# 设置Latin Hypercube Sampling算子
sampling = LHS()
# 从问题problem中随机抽取200个个体
X = sampling(problem, 200).get("X")
# 绘制结果
plotting.plot(X, no_fill=True)
代码执行结果如下图所示:
2.2 选择算子(Selection Operator)
选择算子能够实现遗传算法中的交配选择。在交配的开始前,需要从父母中选择可以进行后续染色体交叉的父母。Pymoo中实现了Random Selection与Tournament Selection两种方法:
- 1、Random Selection选择算子
该算子从当前种群中随机选择用于重组的解,其实现过程使用排列组合来避免重复的个体。比如,我们选择了一个排列(5, 2, 3, 4, 1, 0),此时选择交配的父母组合为(5, 2), (3, 4), (1, 0),这样就可以保证没有父母可以参与两次交配。代码实现如下所示:
from pymoo.operators.selection.rnd import RandomSelection
selection = RandomSelection()
- 2、Tournament Selection选择算子
该算子能够通过引入竞赛压力(Tournament Pressure)来加遗传算法的收敛速度。下面的代码实现了一个二元Tornament选择,即每个比赛有两个人参加。定义了参与者的数量后,需要将获胜者写入输出数组,这里,我们使用适应度来实现。
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.operators.selection.tournament import TournamentSelection
from pymoo.optimize import minimize
from pymoo.problems import get_problem
# 二元Tournament选择的方法
def binary_tournament(pop, P, _, **kwargs):
# P的行数与列数分别定义了竞赛的场数n_tournaments与竞赛者数量n_competitors
n_tournaments, n_competitors = P.shape
if n_competitors != 2:
raise Exception("Only pressure=2 allowed for binary tournament!")
# 二元Tournament选择方法的返回值
import numpy as np
S = np.full(n_tournaments, -1, dtype=np.int)
# 下面执行所有的竞赛
for i in range(n_tournaments):
a, b = P[i]
# 如果第一个个体更好,则选择第一个个体;否则选择第二个
if pop[a].F < pop[b].F:
S[i] = a
else:
S[i] = b
return S
# 设置选择算子
selection = TournamentSelection(pressure=2, func_comp=binary_tournament)
# 设置问题
problem = get_problem("rastrigin")
# 设置遗传算法
algorithm = GA(pop_size=100, eliminate_duplicates=True)
# 执行最小化算法
res = minimize(problem, algorithm, termination=('n_gen', 100), verbose=False)
print(res.X)
2.3 交叉算子(Crossover Operator)
Pymoo中实现五种交叉算子:Simulated Binary Crossover (SBX)、Point Crossover、Exponential Crossover、Uniform Crossover、Half Uniform Crossover (bin_hux, int_hux)。
- 1、模拟二元交叉(SBX, Simulated Binary Crossover)
SBX交叉算则的思路为:实数可以用二进制来表示,然后执行点交叉操作,SBX通过使用 模拟二进制交叉的概率分布模拟此操作。构造一个交叉算子对象的代码如下所示:
from pymoo.operators.crossover.sbx import SBX
crossover = SBX()
交叉算法提供了交叉概率与eta(指数分布相关)参数。下面以一个变量的优化问题为例子,在0.2与0.8两个点之间进行交叉操作,并可视化得到的指数分布,通过eta参数可以对指数分布进行微调。
SBX的概率服从指数分布,需要注意的是为了简便起见,这里设置prob_var=1,即每个变量都参与交叉操作。在实际应用对于两个变量的交叉操作,将prob_var设置为0.5的概率更加合适,即每个父代变量进行交叉的概率均为0.5。
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.sbx import SBX
def show(eta_cross):
problem = Problem(n_var=1, xl=0.0, xu=1.0)
# 设置交叉操作的位置
a, b = Individual(X=np.array([0.2])), Individual(X=np.array([0.8]))
# 设置父代带有交叉位置的数组
parents = [[a, b] for _ in range(5000)]
# 通过交叉算子对象SBX,对问题problem和parents执行交叉操作,得到子代off
off = SBX(prob=1.0, prob_var=1.0, eta=eta_cross).do(problem, parents)
# 得到子代的X值
Xp = off.get("X")
# 绘制结果
plt.hist(Xp, range=(0, 1), bins=200, density=True, color="red")
plt.show()
# 调用show方法,并设置eta_cross为1
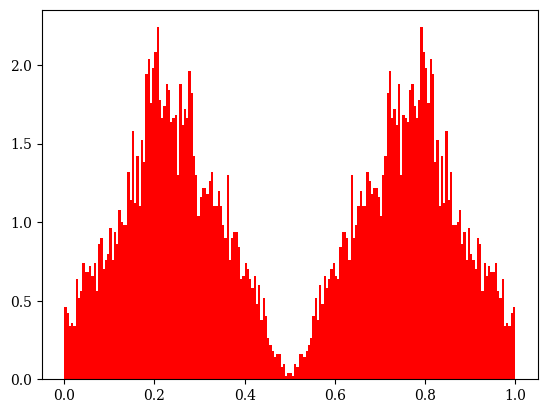
show(1)
代码执行结果如下图所示:
show(30)
结果如下所示:

此外,它还可以用于整数变量。边界稍作修改,再进行交叉后,变量四舍五入。
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.sbx import SBX
from pymoo.operators.repair.rounding import RoundingRepair
def show(eta_cross):
problem = Problem(n_var=1, xl=-20, xu=20)
a, b = Individual(X=np.array([-10])), Individual(X=np.array([10]))
parents = [[a, b] for _ in range(5000)]
off = SBX(prob=1.0, prob_var=1.0, eta=eta_cross, repair=RoundingRepair(), vtype=float).do(problem, parents)
Xp = off.get("X")
plt.hist(Xp, range=(-20, 20), bins=41, density=True, color="red")
plt.show()
show(3)
代码执行结果如下图所示:

- 2、点交叉(Point Crossover)
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.pntx import PointCrossover, SinglePointCrossover, TwoPointCrossover
n_var, n_mating = 50, 30
problem = Problem(n_var=n_var, xl=0.0, xu=1.0, var_type=int)
a, b = Individual(X=np.arange(1, n_var+1)), Individual(X=-np.arange(1, n_var+1))
parents = [[a, b] for _ in range(n_mating)]
def show(M):
plt.figure(figsize=(6, 8))
plt.imshow(M, cmap='Greys', interpolation='nearest')
plt.xlabel("Variables")
plt.ylabel("Individuals")
plt.show()
# 一个点的交叉算子操作
print("One Point Crossover")
off = SinglePointCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_mating] != a.X)
# 两个点的交叉算子操作
print("Two Point Crossover")
off = TwoPointCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_mating] != a.X)
# K 个点的椒炒算子操作,这里以5为例子
print("K Point Crossover (k=5)")
off = PointCrossover(prob=1.0, n_points=5).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_mating] != a.X)
代码执行结果如下所示,
One Point Crossover:
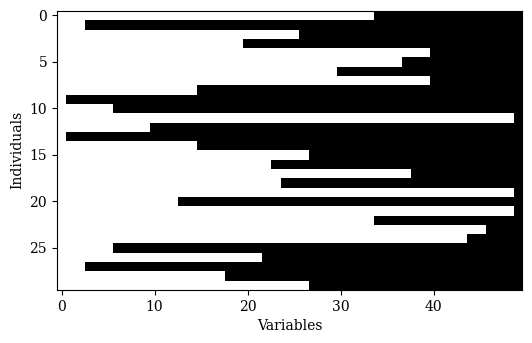
Two Point Crossover:
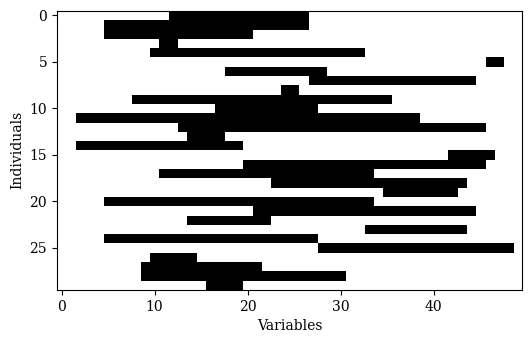
K Point Crossover:
- 3、指数交叉(Exponential Crossover)
指数交叉主要是一点交叉,但偶尔也可以是两点交叉,代码如下所示:
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.expx import ExponentialCrossover
n_var, n_mating = 50, 30
problem = Problem(n_var=n_var, xl=0.0, xu=1.0, var_type=int)
a, b = Individual(X=np.arange(1, n_var+1)), Individual(X=-np.arange(1, n_var+1))
parents = [[a, b] for _ in range(n_matings)]
def show(M):
plt.figure(figsize=(6, 8))
plt.imshow(M, cmap='Greys', interpolation='nearest')
plt.xlabel("Variables")
plt.ylabel("Individuals")
plt.show()
off = ExponentialCrossover(prob=1.0, prob_exp=0.9).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_mating] != a.X)
代码执行结果如下图所示:
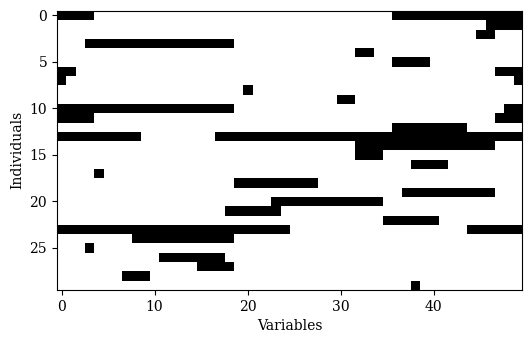
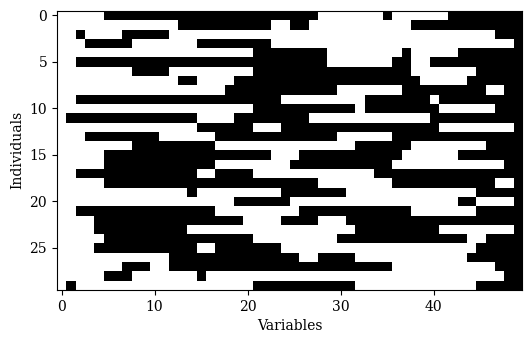
- 4、均匀交叉(Exponential Crossover)
均匀交叉以0.5的概率接受来自每个父项的值,与点交叉不同,它不是采用变量序列,而是采用随机索引。
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.ux import UniformCrossover
n_var, n_mating = 50, 30
problem = Problem(n_var=n_var, xl=0.0, xu=1.0, var_type=int)
a, b = Individual(X=np.arange(1, n_var+1)), Individual(X=-np.arange(1, n_var+1))
parents = [[a, b] for _ in range(n_mating)]
def show(M):
plt.figure(figsize=(6, 8))
plt.imshow(M, cmap='Greys', interpolation='nearest')
plt.xlabel("Variables")
plt.ylabel("Individuals")
plt.show()
off = UniformCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show()
代码执行结果如下图所示:

- 5、半均匀交叉(Half Uniform Crossover)
半均匀交叉算子首先确定第一个和第二个父级中的不同指数,然后从另一个父对象中选择一半的差异,Pymoo的实现代码如下所示:
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.individual import Individual
from pymoo.core.problem import Problem
from pymoo.operators.crossover.hux import HalfUniformCrossover
n_var, n_mating = 100, 100
problem = Problem(n_var=n_var, xl=0.0, xu=1.0, var_type=int)
a = Individual(X=np.full(n_var, False))
b = Individual(X=np.array([k % 5 == 0 for k in range(n_var)]))
parents = [[a, b] for _ in range(n_mating)]
def show(M):
plt.figure(figsize=(6, 8))
plt.imshow(M, cmap='Greys', interpolation='nearest')
plt.xlabel("Variables")
plt.ylabel("Individuals")
plt.show()
off = HalfUniformCrossover(prob=1.0).do(problem, parents)
Xp = off.get("X")
show(Xp[:n_mating] != a.X)
diff_a_to_b = (a.X != b.X).sum()
diff_a_to_off = (a.X != Xp[:n_mating]).sum()
print("Difference in bits (a to b): ", diff_a_to_b)
print("Difference in bits (a to off): ", diff_a_to_off)
print("Crossover Rate: ", diff_a_to_off / diff_a_to_b)
代码执行结果如下图所示:
Difference in bits (a to b): 20
Difference in bits (a to off): 1000
Crossover Rate: 50.0
2.4 突变算子(Mutation Operator)
Pymoo中实现了多项式突变(PM, Polynomial Mutation)算子与位翻转突变(BM, Bitflip Mutation)算子两种方法。
- 1、多项式突变(PM, Polynomial Mutation)算子
多项式突变算子与模拟二元交叉(SBX, Simulated Binary Crossover)算子具有相同的概率分布,Pymoo中实现多项式突变的代码如下所示:
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.pm import PolynomialMutation
def show(eta_mut):
problem = Problem(n_var=1, xl=0.0, xu=1.0)
X = np.full((5000, 1), 0.5)
pop = Population.new(X=X)
mutation = PolynomialMutation(prob=1.0, eta=eta_mut)
off = mutation(problem, pop)
Xp = off.get("X")
plt.hist(Xp, range=(0.0, 1.0), bins=200, density=True, color="red")
plt.show()
show(30)
代码执行结果如下图所示:

同样的,我们可以对离散变量进行多项式突变操作,代码如下所示:
import maplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.pm import PolynomialMutation
from pymoo.operators.repair.rounding import RoundingRepair
def show(eta_mut):
problem = Problem(n_var=1, xl=-20, xu=20)
X = np.full((5000, 1), 0.0)
pop = Population.new(X=X)
mutation = PolynomialMutation(prob=1.0, eta=eta_mut, repair=RoundingRepair())
off = mutation(problem, pop)
Xp = off.get("X")
plt.hist(Xp, range=(-20, 20), bins=40, density=True, color="red")
plt.show()
show(30)
代码执行结果如下图所示:

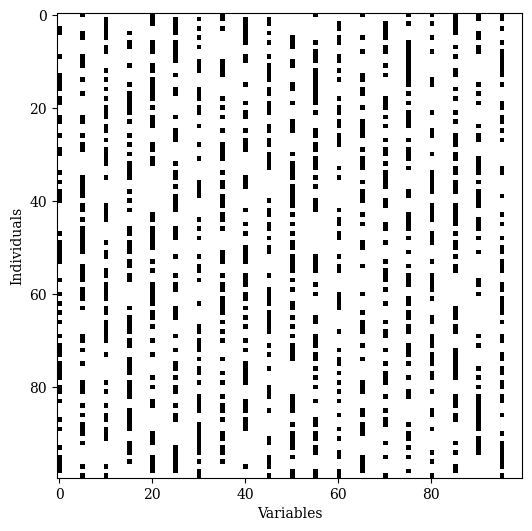
- 2、位翻转突变(BM, Bitflip Mutation)算子
BM随机对一个位进行翻转,以实现突变算子,Pymoo的实现代码如下所示:
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.bitflip import BitflipMutation
n_var, n_mating = 100, 50
problem = Problem(n_var=n_var, vtype=bool)
X = np.full((100, 100), False)
pop = Population.new(X=X)
mutation = BitflipMutation(prob=0.5, prob_var=0.3)
Xp = mutation(problem, pop).get("X")
plt.figure(figsize=(6, 6))
plt.imshow(X != Xp, cmap='Greys', interpoplation='nearest')
plt.show()
代码执行结果如下图所示:
