数据结构【严蔚敏】C语言第二版图章节课后算法题
目录
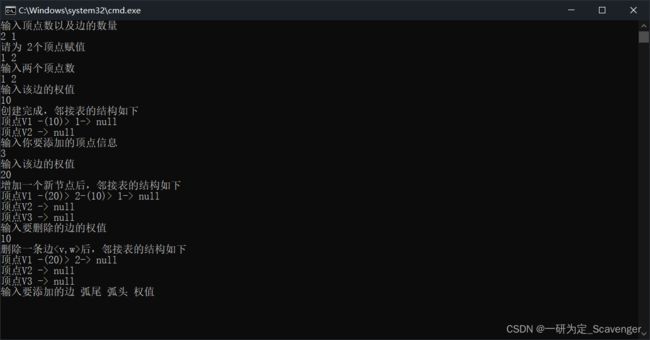
分别以邻接矩阵和邻接表作为存储结构,实现以下图的基本操作
①增加一个新顶点v
④删除一条边后
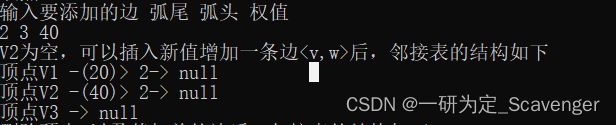
③增加一条边,w>
②删除顶点以及其附属的边编辑
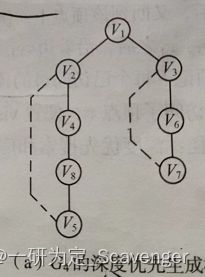
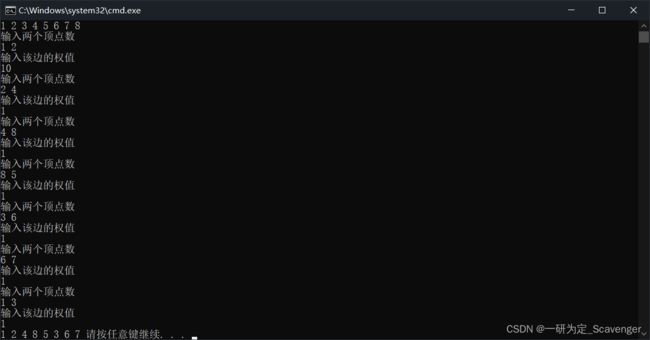
设计算法,实现从顶点v出发的非递归深度优先遍历
设计算法,求图G从V0出发的最短路径中,最大的路径的终点v
判别有向图中Vi到Vj是否存在路径
全部实现代码
分别以邻接矩阵和邻接表作为存储结构,实现以下图的基本操作
①增加一个新顶点v
④删除一条边后
③增加一条边,w>
②删除顶点以及其附属的边编辑
设计算法,实现从顶点v出发的非递归深度优先遍历
设计算法,求图G从V0出发的最短路径中,最大的路径的终点v
判别有向图中Vi到Vj是否存在路径
分别以邻接矩阵和邻接表作为存储结构,实现以下图的基本操作
因为邻接矩阵和邻接表的实现原理上无太大差异,所以这里只给出邻接矩阵表示法
①增加一个新顶点v
void insertNewNode(PGraph G,int Vf,int Vl) //Vf以该顶点为弧头的边 //Vl以该顶点为弧尾的边
{
int & MaxFlag = total; //引用类型 改变MaxFLag同时改变total
G->verNums++;
G->arcNums++; //顶点和边的值都添加
if (G->verNums>total)
{
G->Vertext = lengthenArr(G,MaxFlag);
}
for (int i = G->verNums-1; i > G->verNums-2; i--)
{
G->Vertext[i].verTex = Vl;
G->Vertext[i].firstArc = NULL;
}
//链接两个顶点
int v1Index = Location(G,Vf);
int v2Index = Location(G,Vl);
ParcNode newNode = (ParcNode)malloc(sizeof(arcNode)); //新生成一个边节点
newNode->adjNode = v2Index;
newNode->nextNode = G->Vertext[v1Index].firstArc;
G->Vertext[v1Index].firstArc = newNode; //邻接点建立完成
printf("输入该边的权值\n");
scanf_s("%d",&newNode->weight);
}④删除一条边后
void DeleteArcAndAdj(PGraph G,int Vf) //删除以Vf出发的顶点及其所有的邻接点
{
//先将Vf所有的邻接节点释放最后再将顶点节点删除
int VfIndex = Location(G,Vf);
ParcNode deleteFlag = G->Vertext[VfIndex].firstArc;
int arcFlag = 0; //删除的边数
while (deleteFlag)
{
ParcNode De = deleteFlag;
deleteFlag = deleteFlag->nextNode;
free(De); //将该节点地址删除;
arcFlag++;
}
//分支删除结束.....
//删除顶点表中的顶点
for (int i = VfIndex; i < G->verNums; i++)
{
G->Vertext[i] = G->Vertext[i+1]; //后一个节点的值覆盖前一个节点
}
G->verNums--;
G->arcNums -=arcFlag;
}③增加一条边
bool addNewAdj(PGraph G,int Vf,int Vl,int w)
{
//vf 要增加的边的弧尾 vl 要增加的边的弧头 w 边之间的权值
int vfIndex = Location(G,Vf);
int vlIndex = Location(G,Vl);
//判断这两个顶点是否已经存在边,如果已经存在则添加失败
if(G->Vertext[vfIndex].firstArc ==NULL)
{
printf("V%d为空,可以插入新值",Vf);
}
else
{
ParcNode judgeNode = G->Vertext[vfIndex].firstArc;
while (judgeNode&&judgeNode->weight!=w)
{
judgeNode = judgeNode->nextNode;
}
if (judgeNode->adjNode==vlIndex) //vf和vl之间存在边,直接退出
{
printf("两点之间已存在边,请重新选择两个新的节点\n");
return false;
}
}
//否则 没有新的边开始操作
ParcNode newNode = (ParcNode)malloc(sizeof(arcNode));
newNode->adjNode = vlIndex;
newNode->nextNode = G->Vertext[vfIndex].firstArc;
G->Vertext[vfIndex].firstArc = newNode;
G->arcNums++;
newNode->weight = w;
return true;
}②删除顶点以及其附属的边

bool delOldArc(PGraph G,int Vf,int w)
{
//Vf要删除的边依附的弧尾 w 要删除的边 通过权值来识别
int i = Location(G,Vf);
ParcNode p = G->Vertext[i].firstArc; //设置p指向第一个邻接点
if (p->weight == w)
{
G->Vertext[i].firstArc = p->nextNode; //第一个邻接点就是要删除的节点
free(p);
return true;
}
else
{
while (p->nextNode->weight!=w&&p->nextNode)
{
p = p->nextNode;
}
if(!p->nextNode)
{
return false;//没有找到相关的边
}
else //找到权值为w的上一个邻接点
{
ParcNode del = p->nextNode;
p->nextNode = del->nextNode;
free(del);
return true;
}
}
}设计算法,实现从顶点v出发的非递归深度优先遍历
void DFS(PGraph G,int v) //从顶点v出发的深度优先遍历,非递归
{
Stack S;
Init_Stack(&S,G); //初始化栈
bool visited [10] = {}; //访问数组
int V1 = Location(G,v);
Push(&S,G->Vertext[V1]);
while (!is_empty(&S)) //栈非空
{
verNode out_node = Pop(&S); //栈头元素出栈,访问该顶点值 并将其相关顶点加入
printf("%d ",out_node.verTex);
int index = Location(G,out_node.verTex);
visited[index] = true;
ParcNode p = out_node.firstArc;
while (p)
{
if (!visited[p->adjNode]) //当前顶点没被访问过 才加入
{
Push(&S,G->Vertext[p->adjNode]);
}
p = p->nextNode;
}
}
}设计算法,求图G从V0出发的最短路径中,最大的路径的终点v
int LongestLenVer(int path [],PGraph G)
{
int sum = 0,max = 0,maxver = 0;
//通过邻接表和Path结合来找最短路径
for (int k = 5; k >0; k--) //从第五个顶点开始搜起来
{
int flag = path[k];
printf("顶点%d最短路径为\n",k);
for (int i = path[k]; i>=0; i = path[i])
{
printf("-> %d ",i);
}
printf("\n");
for (;flag>=0;)
{
ParcNode p = G->Vertext[flag].firstArc;
while (p)
{
if (p->adjNode==k)
{
sum+=p->weight;
break;
}
p = p->nextNode;
}
k = flag;
flag = path[flag];
}
if (sum>max)
{
max = sum;
maxver = k;
}
printf("搜寻完毕,顶点%d到V0的最短路径总和为 %d \n",k,sum);
sum = 0;
}
return maxver;
}
void FindMaxShortestLen(PGraph G,int v) //找到从顶点v出发的最短路径长度最大的那个顶点
{
int Path [10] = {},D[10] = {};bool S [10] = {};
int vindex = Location(G,v);
//辅助数组 S[i]//记录当前顶点是否是最短路径上的顶点 Path[i]记录当前顶点的前驱顶点 D[i] 记录当前顶点到v的权值
for (int i = 0; i < G->verNums; i++)
{
ParcNode p = G->Vertext[vindex].firstArc;
S[i] = false;
while (p)
{
if (p->adjNode==i)
{
D[i] = p->weight;
break;
}
p = p->nextNode;
}
if (!p) //如果遍历到结束说明 没有直接相连的顶点 则权值设置为无穷大
{
D[i] = MaxNums;
}
//设置Path值
p = G->Vertext[vindex].firstArc;
while (p)
{
if (p->adjNode==i)
{
Path[i] = vindex;
break;
}
p = p ->nextNode;
}
if (!p) //遍历结束p为空 说明没有路径 path值设为-1
{
Path[i] = -1;
}
}
//初始化完毕
S[vindex] = true;
D[vindex] = 0;
for (int i = 1; i < G->verNums; i++) //合并剩下的n-1个节点
{
int min = MaxNums,w;
for (int j = 0; j < G->verNums; j++)
{
//在D[i] 中找最小权值
if (D[j]verNums; i++)
{
ParcNode p = G->Vertext[w].firstArc;
while (p)
{
if (p->adjNode==i) //从v2有到该顶点的直接连接点,可以判断是否为最小
{
if (p->weight+D[w]weight+D[w];
Path[i] = w; //更新前驱
printf("此次更新权值时,发现V0到%d原路径长度为%d ,在有%d 到 顶点%d之间的路径更短了,更短的权值为 : %d\n\n",i,flag,w,i,D[i]);
}
}
p =p->nextNode;
}
}
}
//
int maxver = LongestLenVer(Path,G);
printf("搜寻结束,从顶点V0出发的最短路径中,路径最长的顶点为:%d",maxver);
} 判别有向图中Vi到Vj是否存在路径
输入顶点V0->V3
bool DFS_Recursion(PGraph G,int Vi,int Vj,bool visited []) //采用递归的方法判断Vi到Vj之间是否存在路径
{
//从Vi出发递归找Vj
visited[Vi] = true;
int Vindex = Location(G,Vi);
int Vjndex = Location(G,Vj);
ParcNode p = G->Vertext[Vindex].firstArc;
while (p&&!visited[Vi])
{
if (p->adjNode==Vjndex)
{
printf("找到Vi和Vj之间的路径");
return true;
}
while(p->nextNode)
{
int w =G->Vertext[p->adjNode].verTex;
DFS_Recursion(G,w,Vj,visited);//一直深度遍历,直到Vi的所有邻接点都遍历完成
p = p->nextNode;
}
}
}全部实现代码
// 图的相关算法题.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "stdlib.h"
#include "stdio.h"
#define Maxsize 4
#define MaxNums 32761
typedef struct arcNode{
int adjNode; //邻接点
arcNode * nextNode; //相同弧尾的下一条弧
int weight;
}arcNode,*ParcNode;
typedef struct
{
int verTex;
arcNode * firstArc; //执行从该顶点出发的第一条邻接点
}verNode,*PverNode;
typedef struct
{
PverNode Vertext;
int arcNums,verNums;
}Graph,*PGraph; //图的结构
typedef struct Stack
{
PverNode node;
int front;
}Stack,*PStack;
void Init_Stack(PStack S,PGraph G)
{
S->node = (PverNode)malloc(sizeof(verNode)*G->verNums);
S->front = -1;
}
void Push(PStack S,verNode node)
{
S->front++;
S->node[S->front] = node;
}
verNode Pop(PStack S)
{
verNode outNode = S->node[S->front];
S->front--;
return outNode;
}
bool is_empty(PStack S)
{
if (S->front == -1)
{
return true;
}
return false;
}
void Init_Graph(PGraph G)
{
printf("输入顶点数以及边的数量\n");
scanf_s("%d %d",&G->verNums,&G->arcNums);
G->Vertext = (PverNode)malloc(sizeof(verNode)*(G->verNums)); //定义一个空间大小为10的数组保存每个顶点
for (int i = 0; i < G->verNums; i++)
{
G->Vertext[i].verTex = 0;
G->Vertext[i].firstArc = NULL;
}
}
int Location(PGraph G,int v)
{
for (int i = 0; i < G->verNums; i++)
{
if(G->Vertext[i].verTex == v)
{
return i;
}
}
return -1;
}
void Create_Graph(PGraph G)
{
printf("请为 %d个顶点赋值\n",G->verNums);
for (int i = 0; i < G->verNums; i++)
{
scanf_s("%d",&G->Vertext[i].verTex);
}
int v1,v2;
for (int i = 0; i < G->arcNums; i++)
{
printf("输入两个顶点数\n");
scanf_s("%d %d",&v1,&v2); //v1 --> v2
int v1Index = Location(G,v1);
int v2Index = Location(G,v2);
ParcNode newNode = (ParcNode)malloc(sizeof(arcNode)); //新生成一个边节点
newNode->adjNode = v2Index;
newNode->nextNode = G->Vertext[v1Index].firstArc;
G->Vertext[v1Index].firstArc = newNode; //邻接点建立完成
//设置权值
printf("输入该边的权值\n");
scanf_s("%d",&newNode->weight);
}
}
PverNode lengthenArr(PGraph G,int &total) //扩展数组
{
PverNode p = G->Vertext;
p = (PverNode)malloc(sizeof(verNode)*2);
total = total*2;
for (int i = 0; i < G->verNums; i++)
{
p[i] = G->Vertext[i]; //重新为数组赋值
}
return p;
}
//①增加一个新顶点v,InsertVex(G,v)
int total = Maxsize; //保存为当前数组的总容量
void insertNewNode(PGraph G,int Vf,int Vl) //Vf以该顶点为弧头的边 //Vl以该顶点为弧尾的边
{
int & MaxFlag = total; //引用类型 改变MaxFLag同时改变total
G->verNums++;
G->arcNums++; //顶点和边的值都添加
if (G->verNums>total)
{
G->Vertext = lengthenArr(G,MaxFlag);
}
for (int i = G->verNums-1; i > G->verNums-2; i--)
{
G->Vertext[i].verTex = Vl;
G->Vertext[i].firstArc = NULL;
}
//链接两个顶点
int v1Index = Location(G,Vf);
int v2Index = Location(G,Vl);
ParcNode newNode = (ParcNode)malloc(sizeof(arcNode)); //新生成一个边节点
newNode->adjNode = v2Index;
newNode->nextNode = G->Vertext[v1Index].firstArc;
G->Vertext[v1Index].firstArc = newNode; //邻接点建立完成
printf("输入该边的权值\n");
scanf_s("%d",&newNode->weight);
}
void DeleteArcAndAdj(PGraph G,int Vf) //删除以Vf出发的顶点及其所有的邻接点
{
//先将Vf所有的邻接节点释放最后再将顶点节点删除
int VfIndex = Location(G,Vf);
ParcNode deleteFlag = G->Vertext[VfIndex].firstArc;
int arcFlag = 0; //删除的边数
while (deleteFlag)
{
ParcNode De = deleteFlag;
deleteFlag = deleteFlag->nextNode;
free(De); //将该节点地址删除;
arcFlag++;
}
//分支删除结束.....
//删除顶点表中的顶点
for (int i = VfIndex; i < G->verNums; i++)
{
G->Vertext[i] = G->Vertext[i+1]; //后一个节点的值覆盖前一个节点
}
G->verNums--;
G->arcNums -=arcFlag;
}
bool delOldArc(PGraph G,int Vf,int w)
{
//Vf要删除的边依附的弧尾 w 要删除的边 通过权值来识别
int i = Location(G,Vf);
ParcNode p = G->Vertext[i].firstArc; //设置p指向第一个邻接点
if (p->weight == w)
{
G->Vertext[i].firstArc = p->nextNode; //第一个邻接点就是要删除的节点
free(p);
return true;
}
else
{
while (p->nextNode->weight!=w&&p->nextNode)
{
p = p->nextNode;
}
if(!p->nextNode)
{
return false;//没有找到相关的边
}
else //找到权值为w的上一个邻接点
{
ParcNode del = p->nextNode;
p->nextNode = del->nextNode;
free(del);
return true;
}
}
}
void show(PGraph G)
{
for (int i = 0; i < G->verNums; i++)
{
printf("顶点V%d ",G->Vertext[i].verTex);
ParcNode p = G->Vertext[i].firstArc; //让p指向第一条邻节点,如果有则输出并且指向下一条邻节点 如果没有则跳出
while(p)
{
printf("-(%d)> %d",p->weight,p->adjNode);
p = p->nextNode;
}
if (!p)
{
printf("-> null \n");
}
}
}
bool addNewAdj(PGraph G,int Vf,int Vl,int w)
{
//vf 要增加的边的弧尾 vl 要增加的边的弧头 w 边之间的权值
int vfIndex = Location(G,Vf);
int vlIndex = Location(G,Vl);
//判断这两个顶点是否已经存在边,如果已经存在则添加失败
if(G->Vertext[vfIndex].firstArc ==NULL)
{
printf("V%d为空,可以插入新值",Vf);
}
else
{
ParcNode judgeNode = G->Vertext[vfIndex].firstArc;
while (judgeNode&&judgeNode->weight!=w)
{
judgeNode = judgeNode->nextNode;
}
if (judgeNode->adjNode==vlIndex) //vf和vl之间存在边,直接退出
{
printf("两点之间已存在边,请重新选择两个新的节点\n");
return false;
}
}
//否则 没有新的边开始操作
ParcNode newNode = (ParcNode)malloc(sizeof(arcNode));
newNode->adjNode = vlIndex;
newNode->nextNode = G->Vertext[vfIndex].firstArc;
G->Vertext[vfIndex].firstArc = newNode;
G->arcNums++;
newNode->weight = w;
return true;
}
void show_xx(int flag,PGraph G)
{
switch (flag)
{
case 0:
printf("创建完成,邻接表的结构如下\n");
show(G);
break;
case 1:
printf("增加一个新节点后,邻接表的结构如下\n");
show(G);
break;
case 2:
printf("删除顶点v以及其相关的边后,邻接表的结构如下\n");
show(G);
break;
case 3:
printf("增加一条边后,邻接表的结构如下\n");
show(G);
break;
case 4:
printf("删除一条边后,邻接表的结构如下\n");
show(G);
break;
default:
printf("error order,can't identify...\n");
break;
}
}
void DFS(PGraph G,int v) //从顶点v出发的深度优先遍历,非递归
{
Stack S;
Init_Stack(&S,G); //初始化栈
bool visited [10] = {}; //访问数组
int V1 = Location(G,v);
Push(&S,G->Vertext[V1]);
while (!is_empty(&S)) //栈非空
{
verNode out_node = Pop(&S); //栈头元素出栈,访问该顶点值 并将其相关顶点加入
printf("%d ",out_node.verTex);
int index = Location(G,out_node.verTex);
visited[index] = true;
ParcNode p = out_node.firstArc;
while (p)
{
if (!visited[p->adjNode]) //当前顶点没被访问过 才加入
{
Push(&S,G->Vertext[p->adjNode]);
}
p = p->nextNode;
}
}
}
int LongestLenVer(int path [],PGraph G)
{
int sum = 0,max = 0,maxver = 0;
//通过邻接表和Path结合来找最短路径
for (int k = 5; k >0; k--) //从第五个顶点开始搜起来
{
int flag = path[k];
printf("顶点%d最短路径为\n",k);
for (int i = path[k]; i>=0; i = path[i])
{
printf("-> %d ",i);
}
printf("\n");
for (;flag>=0;)
{
ParcNode p = G->Vertext[flag].firstArc;
while (p)
{
if (p->adjNode==k)
{
sum+=p->weight;
break;
}
p = p->nextNode;
}
k = flag;
flag = path[flag];
}
if (sum>max)
{
max = sum;
maxver = k;
}
printf("搜寻完毕,顶点%d到V0的最短路径总和为 %d \n",k,sum);
sum = 0;
}
return maxver;
}
void FindMaxShortestLen(PGraph G,int v) //找到从顶点v出发的最短路径长度最大的那个顶点
{
int Path [10] = {},D[10] = {};bool S [10] = {};
int vindex = Location(G,v);
//辅助数组 S[i]//记录当前顶点是否是最短路径上的顶点 Path[i]记录当前顶点的前驱顶点 D[i] 记录当前顶点到v的权值
for (int i = 0; i < G->verNums; i++)
{
ParcNode p = G->Vertext[vindex].firstArc;
S[i] = false;
while (p)
{
if (p->adjNode==i)
{
D[i] = p->weight;
break;
}
p = p->nextNode;
}
if (!p) //如果遍历到结束说明 没有直接相连的顶点 则权值设置为无穷大
{
D[i] = MaxNums;
}
//设置Path值
p = G->Vertext[vindex].firstArc;
while (p)
{
if (p->adjNode==i)
{
Path[i] = vindex;
break;
}
p = p ->nextNode;
}
if (!p) //遍历结束p为空 说明没有路径 path值设为-1
{
Path[i] = -1;
}
}
//初始化完毕
S[vindex] = true;
D[vindex] = 0;
for (int i = 1; i < G->verNums; i++) //合并剩下的n-1个节点
{
int min = MaxNums,w;
for (int j = 0; j < G->verNums; j++)
{
//在D[i] 中找最小权值
if (D[j]verNums; i++)
{
ParcNode p = G->Vertext[w].firstArc;
while (p)
{
if (p->adjNode==i) //从v2有到该顶点的直接连接点,可以判断是否为最小
{
if (p->weight+D[w]weight+D[w];
Path[i] = w; //更新前驱
printf("此次更新权值时,发现V0到%d原路径长度为%d ,在有%d 到 顶点%d之间的路径更短了,更短的权值为 : %d\n\n",i,flag,w,i,D[i]);
}
}
p =p->nextNode;
}
}
}
//
int maxver = LongestLenVer(Path,G);
printf("搜寻结束,从顶点V0出发的最短路径中,路径最长的顶点为:%d",maxver);
}
bool DFS_Recursion(PGraph G,int Vi,int Vj,bool visited []) //采用递归的方法判断Vi到Vj之间是否存在路径
{
//从Vi出发递归找Vj
visited[Vi] = true;
int Vindex = Location(G,Vi);
int Vjndex = Location(G,Vj);
ParcNode p = G->Vertext[Vindex].firstArc;
while (p&&!visited[Vi])
{
if (p->adjNode==Vjndex)
{
printf("找到Vi和Vj之间的路径");
return true;
}
while(p->nextNode)
{
int w =G->Vertext[p->adjNode].verTex;
DFS_Recursion(G,w,Vj,visited);//一直深度遍历,直到Vi的所有邻接点都遍历完成
p = p->nextNode;
}
}
}
int _tmain(int argc, _TCHAR* argv[])
{
Graph G;
int newNode,weight,Vf,Vl;
Init_Graph(&G);
Create_Graph(&G);
bool visited [10] = {};
if(DFS_Recursion(&G,2,4,visited))
{
printf("存在路径");
}
else
{
printf("不存在路径");
}
}