基于Matlab的随机信号分析

  1、产生均值为1，方差为4的高斯随机分布函数，并求最大值、最小值、均值和方差。

N = random('Normal', 0, 4, 1, 1024);
x = max(N);
y = min(N);
m = mean(N);
v = var(N);
plot(N)

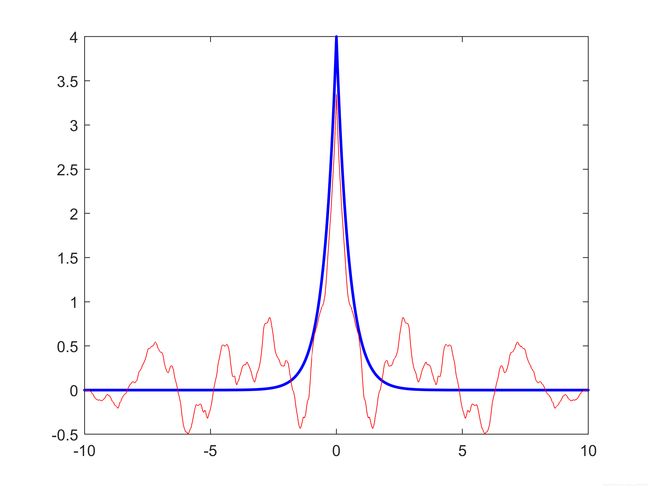
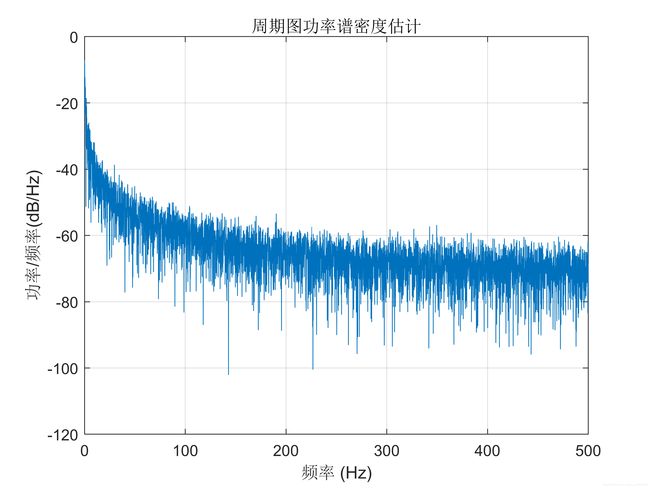
  2、产生协方差函数为：$$C(t)=4e^{-2|t|}$$的平稳高斯过程的样本函数。估计所产生样本的时间自相关函数和功率谱密度，并统计自相关函数和功率谱密度。

N = 10000;
T = 0.001;
sig = 2;
bet = 2;
m = exp(-bet * T);
n = sig * sqrt(1 - m * m);
p = normrnd(0, 1, [1,N]);
x = zeros(1,N);
x(1) = sig * p(1);

for i = 2:N
    x(i) = m * x(i-1) + n * p(i);
end

R = xcorr(x) / N;
q = [-N+1:N-1];
R0 = (sig ^ 2) * exp(-bet * abs(q * T));
y = filter(n, m, x);

plot(q * T, R0, 'b.', q * T, R, 'r');
periodogram(y, [], N, 1/T);

  3、仿真一个平均功率为1的白噪声通带系统，白噪声为高斯分布，带通系统的两个截至频率分别为3KHZ和4KHZ，求自相关函数和功率谱密度。

N = 500;
m =  random('norm', 0, 1, 1, N);
n = fir1(101, [0.3,0.4]);
H1 = fft(n, 2*N);
Rx = xcorr(m, 'biased');
Sx = abs(fft(m, 2*N) .^ 2) / (2*N);
H2 = abs(H1) .^ 2;
Sy = Sx .* H2;
Ry = fftshift(ifft(Sy));
p = (1:N) / N;
t = (-N:N-1) / N*(N/20000);

subplot(4,1,1);plot(p , abs(Sx(1:N)));
subplot(4,1,2);plot(p , abs(H2(1:N)));
subplot(4,1,3);plot(p , abs(Sy(1:N)));
subplot(4,1,4);plot(t , Ry);