深度贝叶斯神经网络
深度贝叶斯神经网络
翻译自:博客
传统的神经网设计得不好,无法建模他们所做的预测相关的不确定性。为此,有一种方法是完全的贝叶斯
这里是我对下列三种方法的看法:
- 使用MCMC估计积分
- 使用黑箱变分推断(edward框架)
- 使用MC dropout
但是首先,我们先做什么呢?
深度学习网络都有很多参数,通常权重用 w 1 , w 2 , . . . w_1, w_2,... w1,w2,...表示,偏置用 b 1 , b 2 , . . . b_1,b_2,... b1,b2,...表示。传统的(非贝叶斯)方法仅仅通过最大似然估计来学习参数的最优值。这些值是标量,比如 w 1 = 0.8 , b 1 = 3.1 w_1=0.8, b_1=3.1 w1=0.8,b1=3.1
另一个方面,贝叶斯方法关注每个参数的分布。例如,在贝叶斯神经网络训练收敛之后,上面两个参数可以被这两个高斯曲线描述。
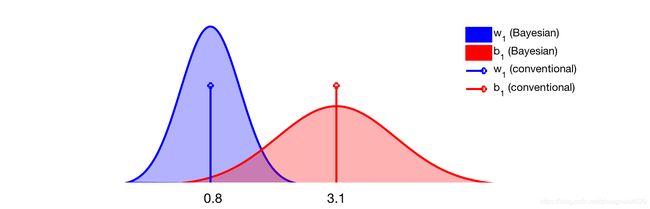
贝叶斯网络训练完成之后, w 1 , b 1 w_1, b_1 w1,b1就可以表示为高斯曲线,如果是传统的网络,表示为两条线。
表示为一个分布而不是一个单一的值,这是很重要的事情。一方面,它使得从分布中多次取样成为可能,还可以看到随之带来的模型预测的变化。如果它给出连续的预测,一遍遍采样后,网络会对它的预测更有“信心”。
难点
估计分布当然是最难的部分,通过使用贝叶斯法则,我们可以转化为计算后验概率密度。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传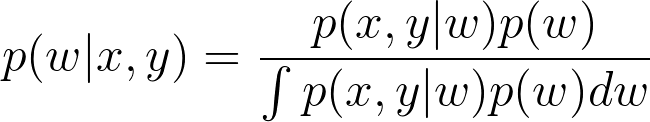
贝叶斯法则,x和y分别输入和输出,分母的积分需要对所有的 w w w可能的取值计算边缘分布,这是最难的部分。
问题在于分母——也被叫做模型的证据,这需要对参数全部可能的值进行积分(也就是说全部非权重和偏置取值空间),实践中这不太可行。
因此,我们采用伪数值的方法来估计积分。
使用MCMC估计积分
由于使用贝叶斯法则计算精确的积分比较困难,MCMC(Markov Chain Monte Carlo)被用于做估计。MCMC背后的想法是非常优美的,我建议阅读这个帖子,里面给出了代码和一些方法的理解。在所有的三个方法里面,除了数学,这个方法是最慢的而且最不sexy的。
优点:理论上MCMC追得到最好的结果,就是说最精确的估计。
缺点:很长时间才能收敛
使用黑箱变分推断(例如edward)
变分推断是一种估计密度函数的方法,它首先选择一个我们已知的分布(例如高斯分布),然后渐进式地改变它的参数,直到它看起来像我们想要计算的分布,也就是后验分布。改变参数不再需要令人苦恼的积分运算,这是一个优化过程,微分比积分通常更容易估计。我们优化的这种“编造”出来的分布,成为变分分布
有一些优雅的数学展示了挑选最优参数为什么等价于最大化下确界的,在某些时候得要检查一下。但是如果你想要直到这种方法具体怎么实现,按时离开理论分析,我准备了一个简短的入门教程,这是一个使用edward的8分类的任务。
# Define:
# ~ K number of classes, e.g. 8
# ~ D size of input, e.g. 10 * 40
# ~ BATCH_SIZE, N_TRAIN, N_TEST, STEPS (how many training steps)
# Tensorflow Placeholders:
w = Normal(loc=tf.zeros([D, K]), scale=tf.ones([D, K]))
b = Normal(loc=tf.zeros(K), scale=tf.ones(K))
x = tf.placeholder(tf.float32, [None, D])
y = Categorical(tf.matmul(x,w)+b)
y_ph = tf.placeholder(tf.int32, [BATCH_SIZE]) # For the labels
我们选择高斯来设置变分分布,然后我们挑选基于KL散度的推断方法。实际上KL的估计是通过“黑箱”变分方法估计ELBO实现的。(如果你对此感兴趣,可以阅读这里)
qw = Normal(loc=tf.Variable(tf.random_normal([D, K])),
scale=tf.nn.softplus(tf.Variable(tf.random_normal([D, K]))))
qb = Normal(loc=tf.Variable(tf.random_normal([K])),
scale=tf.nn.softplus(tf.Variable(tf.random_normal([K]))))
inference = ed.KLqp({w: qw, b: qb}, data={y: y_ph})
inference.initialize(n_iter=STEPS, n_print=100, scale={y: N_TRAIN / BATCH_SIZE})
在定义模型之后,我们现在可以开启tf的session进行训练了。
sess = tf.InteractiveSession()
tf.global_variables_initializer().run()
train_data_generator = generator(train_data, BATCH_SIZE)
train_labs_generator = generator(train_labels, BATCH_SIZE)
for _ in range(inference.n_iter):
X_batch = next(train_data_generator)
Y_batch = next(train_labs_generator)
info_dict = inference.update(feed_dict={x: X_batch, y_ph: Y_batch})
inference.print_progress(info_dict)
我们可以采样这些分布( q w qw qw表示权重, q b qb qb表示偏置),可以看到预测出的是一个分布,这表示了模型的不确定性。
你可以尝试一下porb_lst和samples的用法。
总结如下,优点:它比朴素的MCMC更快,像edward这样的库帮助实现贝叶斯网络,在几分钟之内就可以运行。
缺点:深度贝叶斯网络可能会很慢,而且性能并不能保证始终达到最优。
使用MC dropout
MC dropout 是一项最新的理论发现,它提供了被称为“dropout”的正则化技术的解释,下面再做详细说明。变分推断是一种贝叶斯方法,用于使用任意分布(先前提到的“变分分布”)来估计后验分布;droupout,恰恰相反,它是一种神经网络的正则化方法,训练过程中神经元随机开启或关闭,以免使得网络依赖某个特定的神经元。这是MC dropout的核心思想:dropout能够用于执行变分推断,这里变分分布就是一种伯努利分布(状态为“开”和“关”)。“MC”表示dropout用一种类似于蒙特卡罗的方式采样。在实践中,通过MC dropout 使用将传统的网络转变成贝叶斯网络,使得训练问题变得跟在每层使用ddropout一样简单。这个等价于从伯努利分布中采样,提供一种模型不确定性的度量(多次采样的做的预测的连续性。)当然我们也可以使用其他的变分分布来实现。
优点:容易将一有的深度网络转变成贝叶斯网络,它比其他方法更快,不需要推断框架。
缺点:测试阶段的采样对实时应用来说计算太昂贵了。
那到底贝叶斯神经网络有什么用呢?
许多研究者还是不相信应该这么费力的去使用贝叶斯方法,让我再多说两句,我在自动驾驶部门工作,所有下面这些的例子非常贴切。假想一个人正在驾驶者一辆最新的,最强大的自动驾驶的汽车,当未识别的物体突然出现在驾驶员面前时,比如是一辆飞行汽车,从未在飞行汽车这个类别上受过训练的计算机视觉算法,会把它看作是飞机,认为它在很远的距离上。
那么会发生什么呢?
传统的网络可能会过分自信的误判飞行器的位置,而贝叶斯网络则可以利用其不确定性做出建议放慢速度的决策。
下面举一个最简单的基于Dropout的贝叶斯神经网络的例子:
Input-FC-Relu-Dropout-FC-Relu-Dropout-FC-Logit-Softmax
在这样一个包含两个隐藏层的FC分类网络中,我们接入了dropout层,dropout层的每个神经元以
的概率取0(随机失活)。我们为了得到一个贝叶斯神经网络,按如下进行训练和测试:
- 训练时,打开dropout层,前向推理计算分类损失,基于反向梯度传播算法更新模型参数,迭代若干个epochs
- 测试时,仍然打开dropout层,进行n次前向推理,得到每次的分类概率 p i ∈ R C p_i \in R^C pi∈RC, 其中C是类别数量,最终的分类概率为 p ^ = 1 n ∑ p i \hat{p} = \frac{1}{n}\sum p_i p^=n1∑pi, 分类的不确定度(请大家想想这是哪种不确定度呢?)为 v a r ( p ) = 1 n ∑ ( p i − p ^ ) 2 var(p) = \frac{1}{n}\sum(p_i-\hat{p})^2 var(p)=n1∑(pi−p^)2