Python - matplotlib - 如何探索两个变量间关系？

一、序言

随着各种组学技术的发展，一个样本可能对应成千上万个变量，现阶段研究往往是实践先于理论，通过层层特征筛选，得到少数可能和结局有关的变量，然后再去研究这些变量具体的含义。其中变量间的相互的关系也是研究的一个内容。通过肉眼直接分析原始的数据不太可能能看出变量间的关系，因此往往需要借助图像，以更直观地方式展现变量的分布情况。

二、实战演示

假设经过前期研究，得到了500个数据的两个变量 n, r，，没有任何关于它们对应的总体的信息。现在需要分析这两个变量间的关系
画图前，先选个好看点的预设图像风格：

import matplotlib.pyplot as plt
plt.style.use('ggplot')

1. 直方图

对于一组数据，统计描述的第一步是绘制频数直方图，在matplotlib中，使用hist()函数来绘制。几个关键的参数是：
x： 原始数据的sequence，可输入的数据类型为列表（list）、元组（tuple）、pandas序列（series）、numpy数组（array）等
bins： 箱，当输入值为整数时，表示需要绘制的频数直方图的组数；当输入为一个sequence时，表示定义的每组的界值，如输入[1, 2, 3 ,4]表示分成三组，[1, 2)、[2, 3)、[3, 4]
range： 用于设定bins的左侧边界和右侧边界，例如bins = 3, range = (1,4)，则产生三组，每组界值为[1, 2)、[2, 3)、[3, 4]；当bins输入为sequence时，这条指令无效。
density： 默认为False，如果设置为True，则绘制频率密度直方图。

fig, ax = plt.subplots()
ax.hist(n, bins = 18, range = (-50, 40), label = 'unknown distribution1')
ax.hist(r, bins = 18, range = (-50, 40), label = 'unknown distribution2', alpha = 0.8)
ax.legend()
plt.show()

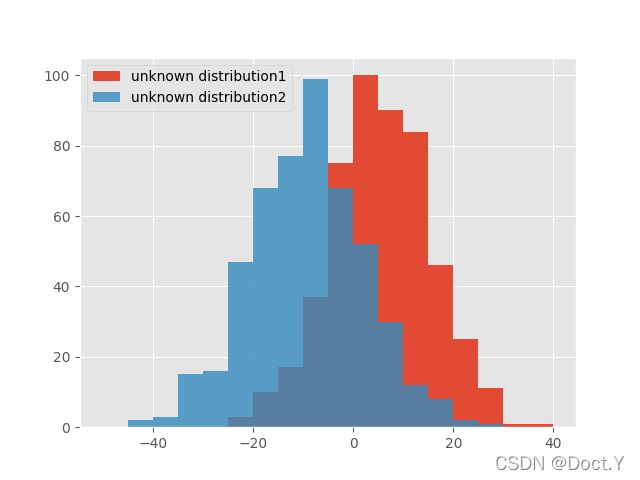
然而直方图并不能看出这两个特征有什么关系，因此接下来选择直方图的升级版

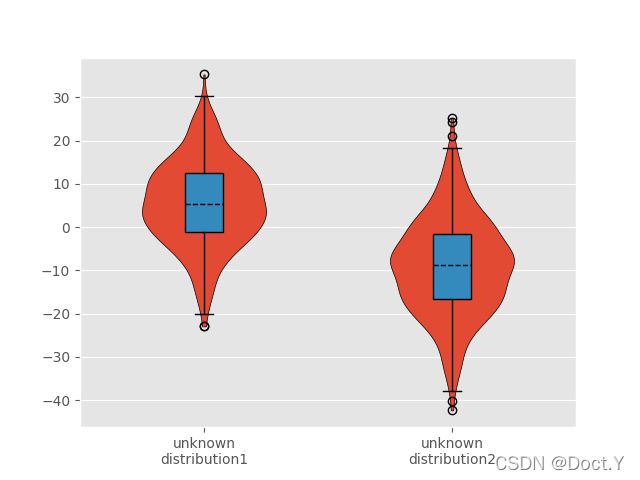
2. 箱型图和小提琴图

https://matplotlib.org/stable/api/_as_gen/matplotlib.axes.Axes.boxplot.html

     Q1-1.5IQR   Q1   median  Q3   Q3+1.5IQR
                  |-----:-----|
  o      |--------|     :     |--------|    o  o
                  |-----:-----|
flier             <----------->            fliers
                       IQR

一个箱型图大概长这样，每一条线是和百分位数有关，flier表示离群值或者异常值。
小提琴图就相当于把直方图旋转90°在取对称。
在matplotlib中，boxplot()用于绘制箱型图，violinplot()用于绘制小提琴图。

violins = ax.violinplot(
	(n, r), 
	showmeans = False, 
	showextrema = False, 
	showmedians = False
	)
for violin in violins['bodies']:
	violin.set_edgecolor('black')
	violin.set_alpha(1)
	
boxes = ax.boxplot(
	(n, r), 
	positions = (1,2), 
	patch_artist = True, 
	medianprops = {'linestyle':'--', 'color':'black'}
	)
ax.set_xticklabels(labels = ['normal\ndistribution', 'unknown\ndistribution'])
ax.grid(axis = 'x')
plt.show()

直方图的升级版也并不能看出这两个特征有什么关系

3. 散点图

每个样本的这两个特征是相互匹配的，因此以n为x轴，r为y轴，绘制的点就代表每一个样本。
在matplotlib中，用scatter()绘制散点图

ax.scatter(n, r)
ax.set_xlabel('n')
ax.set_ylabel('r')
plt.show()

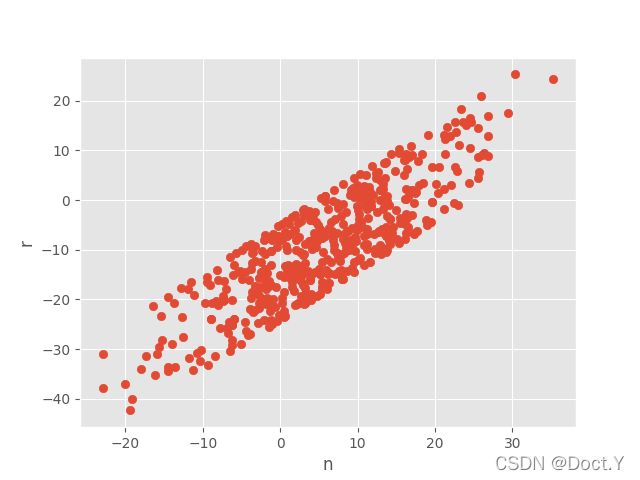
豁然开朗，原来这两个变量是呈现强的线性关系，使用直线回归验证我们的观点

from scipy.stats import linregress
statistics = linregress(n,r)
print(statistics)
'''
LinregressResult(
slope=0.9748791206336714, 
intercept=-14.490971785425117, 
rvalue=0.8537217995118889, 
pvalue=3.1209429808110146e-143, 
stderr=0.026645986874802068, 
intercept_stderr=0.3018466146896383
)
'''

可以看出，相关系数r为0.854，p为10的-143次方基本上等于0，表现出很强的相关性。那么到底n和r是什么分布呢？

import numpy as np
np.random.seed(1)
n = np.random.normal(5, 10, 500)
r = n - np.random.randint(5, 25, 500)

其实n是一个均数为5，标准差为10的正态分布，而r是n随机减掉5-25之间的一个值得到的。在直线回归结果中可以看到，斜率为0.975，相当于1；截距为-14.491，正好在-25和-5的中位数附近。结果和r的推导式基本一样。

三、结语

最原始的最简单，散点图通过把每个样本的值都画出来，能很直观地看出变量的关系。