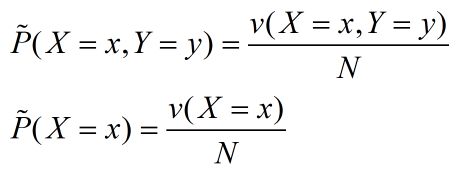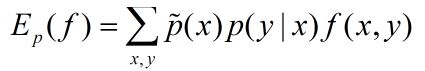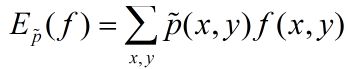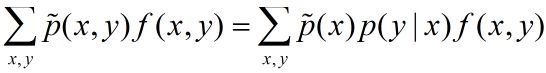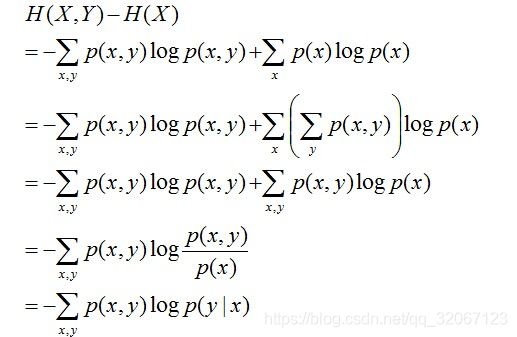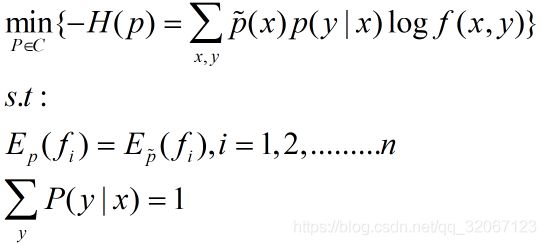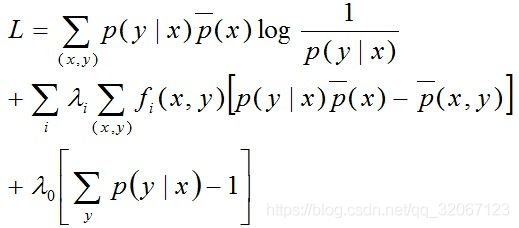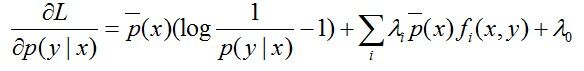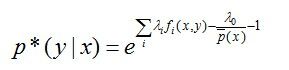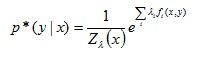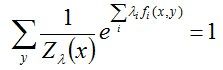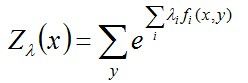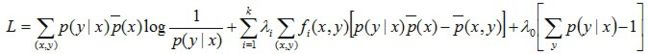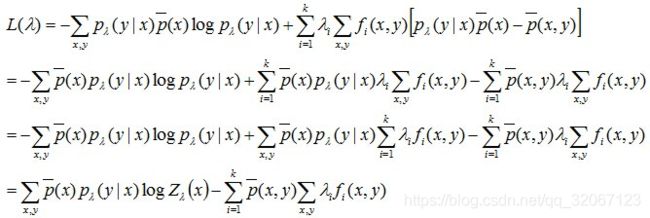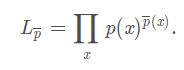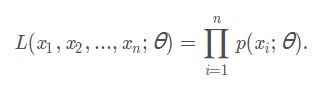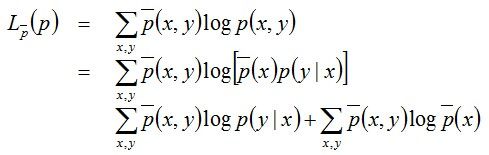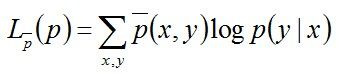机器学习之最大熵模型
最大熵模型的详细推导（参考李航老师机器学习）
- 1.最大熵的原理
- 2.最大熵模型的定义
- 3.最大熵模型的学习
-
-
- 3.1转换为对偶问题
-
- 4.最大熵模型的极大似然估计
- 5.参考文献
1.最大熵的原理
最大熵的原理是概率模型学习的一个准则，最大熵原理认为，学习概率模型时，在所有可能的概率模型中，熵最大的模型是最好的模型。通常用约束条件来确定概率模型的集合，所以，最大熵模型也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
假设离散型随机变量X的概率分布是P(X)，则熵是：
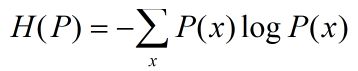
我们学习的目的就是在可能的模型集合中选择最优的模型，而最大熵准则则给出最优模型选择的一个准则。
2.最大熵模型的定义
最大熵原理是统计学习的一般原理，将他应用到分类得到最大熵模型。
假设分类模型是一个条件概率分布 P(Y|X) ，这个模型表示的是对于给定的输入 x 以条件概率 P(Y|X）输出 Y . 即 P(Y|X) 就是我们所要求解的模型。
我们首先考虑模型应该满足的条件，在给定的任意训练数据集中，可以确定确定联合分布 P(X,Y) 的经验分布和边缘分布 P(X) 的经验分布（P(X) 的经验分布指的是样本 X在训练集中出现的概率，是一个确切的值），这里分别以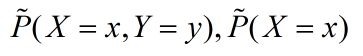 
表示，其中：
其中 v(X=x,Y=y) 表示训练数据集中样本 (x,y) 出现的频数，v(X=x) 表示训练数据集中样本 x 出现的频数，N 表示训练样本的总个数。
使用特征函数 f(x,y) 描述输入 x 和输出 y 之间的某一个事实。其定义为：
当x和y满足这个事实时取值为1，否则取值为0。
特征函数 f(x,y) 关于模型 P(Y|X) 与经验分布
的期望值如下：
特征函数 f(x,y) 关于经验分布
的期望值为：
如果模型能够获取训练数据中的信息，那么就可以假设这两个期望值相等，即：
我们将上式称作模型学习的约束条件， 假设有 n 个特征函数，那么就有 n 个约束条件。
我们知道条件熵等于：
所以，在最大熵模型中条件概率分布 P(Y|X) 上的条件熵为：
即在给定条件下求解 H( P)最大的模型，称之为最大熵模型。
3.最大熵模型的学习
通过上面我们知道只要求解出最大的H( P)锁对应的模型的即可。最大熵模型的学习是带有上述约束条件的，所以等价于约束最优化问题，按照最优化的习惯，我们转化成求解最小值的问题：
关于带有约束的最优化问题我们通常使用拉格朗日乘子，将其转换成无约束最优化的对偶问题。
3.1转换为对偶问题
写出引入拉格朗日函数：
然后求偏导:
注：上面这里是对P(y|x)求偏导，即只把P(y|x)当做未知数，其他都是常数。因此，求偏导时，只有跟P(y0|x0)相等的那个"(x0,y0)"才会起作用，其他的(x,y)都不是关于P(y0|x0)的系数，是常数项，而常数项一律被“偏导掉”了。
另偏导结果等于零可得：
进一步转化：
其中，Z(x)称为规范化因子。
根据之前的约束条件之一：
= 1，所以有：
现将求得的最优解P*(y|x)带回之前建立的拉格朗日函数L
我们得到关于λ的式子：
把之前得到的结果
代入计算即可
至此，我们求得了对偶函数的解析解。
4.最大熵模型的极大似然估计
我们需要考虑的问题是为什么求解熵最大的模型就是最好的模型呢？？ 我们通过证明能得到对偶函数的极大化等价于最大熵模型的极大似然估计。且根据MLE的正确性，可以断定：最大熵的解（无偏的对待不确定性）同时是最符合样本数据分布的解，进一步证明了最大熵模型的合理性。两相对比，熵是表示不确定性的度量，似然表示的是与知识的吻合程度，进一步，最大熵模型是对不确定度的无偏分配，最大似然估计则是对知识的无偏理解。
在给出推导之前我看李航老师的书中直接给出的对数似然公式类似是这样的：
这称之为对数似然函数的一般形式，但为什么是这样的呢？？？借鉴其他博客，给出下面给出解释，一般书上描述的最大似然函数的一般形式是各个样本集X中各个样本的联合概率:
下面继续推导，对数似然的式子为：
对上式两边取对数可得：
因上述式子最后结果的第二项是常数项（因为第二项是关于样本的联合概率和样本自变量的式子，都是定值），所以最终结果为：
至此，我们发现极大似然估计和条件熵的定义式具有极大的相似性，故可以大胆猜测它们极有可能殊途同归，使得它们建立的目标函数也是相同的。 我们来推导下，验证下这个猜测。
将之前得到的最大熵的解带入MLE，计算得到（右边在左边的基础上往下再多推导了几步）：
跟之前得到的对偶问题的极大化解：
只差一个“-”号，所以只要把原对偶问题的极大化解也加个负号，等价转换为对偶问题的极小化解：
则与极大似然估计的结果具有完全相同的目标函数。
换言之，之前最大熵模型的对偶问题的极小化等价于最大熵模型的极大似然估计。
5.参考文献
- 《统计学习方法 李航著》；
- https://blog.csdn.net/v_JULY_v/article/details/40508465
- https://blog.csdn.net/wkebj/article/details/77965714