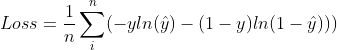李宏毅深度学习HW2 收入预测 (logistic regression)

1.任务内容

• 任务：根据一个人的年龄，工作类型，教育程度等18个特征做一个二分分类——判断其收入是否大于50k。train.csv文件打开如下：

• 训练集（X_train文件中）：32561个人，106（扩展后，见2.1）个特征。

这里首先弄清了一个概念——回归​：在我们认知（测量）这个世界的时候，我们并不能得到这个世界的全部信息（真值），只能得到这个世界展现出的可被我们观测的部分信息。那么，如果我们想得到世界的真值，就只能通过尽可能多的信息，从而使得我们的认识，无限接近（回归）真值。

简单来说，就将现有的数据向假设的模型拟合逼近。

2.实现代码详解

实例代码构建了一层的神经网络，输出层神经元为logistic unit，使用交叉熵损失函数。

1.数据预处理

首先这个任务有个很值得考虑的问题是，如何处理那些非数字的数据。一个似乎可行的办法是，给每类一个数字标记，如教育程度（小学，中学，大学）可以对应（1，2，3），这个方法的问题在于，会给算法暗示相邻数字对应的种类间存在某种联系，而实际上这种联系是不存在的。

另一种方法是作业使用的，把一个特征扩展到多个特征，教育程度扩展成小学，中学，大学等，每个特征用（0，1）标记。经此处理后，特征便从18维度被扩展到了106维，非数的特征也变为了数字。

还有一个处理数据的思路，把fnlwgt（final analysis weights）按区间扩展到多个特征，同样用（0，1）标记，这个操作成为离散化（Discretization）。

2.数据读取

由于作业没给验证集，可以自己划分一个。

def train_dev_split(X, y, dev_size=0.25):
    #按一个比例分出一部分验证集
    train_len = int(round(len(X)*(1-dev_size)))
    return X[0:train_len], y[0:train_len], X[train_len:None], y[train_len:None]

x = np.genfromtxt('X_train',delimiter=',',skip_header=1) 
y = np.genfromtxt('Y_train',delimiter=',',skip_header=1)

3.归一化

常见的利用最大最小值归一，和利用均值方差归一。还没太理解后者为何能归一，希望能找一下相关数学证明。

归一时跳过值为（0，1）的特征，可以省一点时间。（相比上个实验用for循环，改了下边的写法之后...已经足够快了）

#min max归一
col = [0,1,3,4,5,7,10,12,25,26,27,28]
xmin = np.min(x, axis = 0)
xmax = np.max(x, axis = 0)
x[:,col] = (x[:,col]-xmin[col])/(xmax[col] - xmin[col])#快了0.03-0.01=0.02s
'''
#mean std归一
'''
xmean = np.mean(x,axis = 0)
xstd = np.std(x, axis = 0)
col = [0,1,3,4,5,7,10,12,25,26,27,28]
x[:,col] = (x[:,col]-xmean[col])/xstd[col]
'''
x, y, X_dev, Y_dev = train_dev_split(x, y)

 4.参数设定

zeros(n)为n维数组 = zeros((n,))，只有括号里两个参数时才生成二维数组

w = np.zeros(x.shape[1],) #106
b = np.zeros(1,) #1
lamda = 0.001 #正则化惩罚过拟合
max_iter = 40 #迭代次数
batch_size = 32 #number to feed in the model for average to avoid bias
learning_rate = 0.2
num_train = len(y)
num_dev = len(y_test)
step =1
loss_train = [] #训练集损失
loss_validation = [] #测试集损失
train_acc = [] #训练集准确率
test_acc = [] #测试集准确率

5.训练

• 函数

怪不得编辑器自动生成的是xrange，不同的库用的数组类型不一样，返回的对象也不一样。如果是py的range()就不支持np.random的shuffle方法。

log0会出现nan，exp(800)会得到inf，需要注意这种计算错误和处理方法。

def shuffle(X, Y):
    #打乱X,Y
    randomize = np.arange(len(X))
    np.random.shuffle(randomize)
    return (X[randomize], Y[randomize]) #ndarray的参数是数组时，返回一个依参数排序后的数组

def sigmoid(z):
     # Use np.clip to avoid overflow\超出的部分就把它强置为边界部分
     # e是科学计数法的一种表示 aeN: a*10的N次方
    s = np.clip(1 / (1.0 + np.exp(-z)), 1e-6, 1-1e-6)
    return s

def get_prob(X, w, b):
    # the probability to output 1
    return sigmoid(np.add(np.matmul(X, w), b))

def loss(y_pred, Y_label, lamda, w):
    #ypred不可能为1，0，所以就不用防止log0出现nan？
    cross_entropy = -np.dot(Y_label, np.log(y_pred))-np.dot((1-Y_label), np.log(1-y_pred))
    return cross_entropy + lamda * np.sum(np.square(w))

def accuracy(Y_pred, Y_label):
    return np.sum(Y_pred == Y_label)/len(Y_pred)

• 训练主程序

统计数据有可能存在一些隐形的顺序，比如可能没注意的时候数据其实是先统计了男后统计了女。为避免模型学习到这些不相干因素，先得打乱数据顺序。

用了mini-batch的方法，每次选一部分样本来更新参数。

根据步数减少学习率，似乎是adagrad方法思路的简单处理版本。

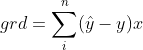交叉熵函数的梯度函数在使用logistic时和二次代价是相同的

for epoch in range(max_iter):
    # Random shuffle for each epoch
    x, y = shuffle(x, y) #打乱各行数据，这样参数能不易陷入局部最优，模型能够更容易达到收敛。     

    # Logistic regression train with batch
    for idx in range(int(np.floor(len(y)/batch_size))): #每个batch更新一次
        x_bt = x[idx*batch_size:(idx+1)*batch_size] #32*106
        y_bt = y[idx*batch_size:(idx+1)*batch_size] #32*1

        # Find out the gradient of the loss
        y_bt_pred = get_prob(x_bt, w, b) #matmul：二维数组间的dot
        pred_error = y_bt - y_bt_pred
        w_grad = -np.mean(np.multiply(pred_error, x_bt.T), 1)+lamda*w #multiply：数组和矩阵对应位置相乘，输出与相乘数组/矩阵的大小一致
        b_grad = -np.mean(pred_error)

        # gradient descent update
        # learning rate decay with time
        w = w - learning_rate/np.sqrt(step) * w_grad
        b = b - learning_rate/np.sqrt(step) * b_grad
        step = step+1

    # Compute the loss and the accuracy of the training set and the validation set
    y_pred = get_prob(x, w, b)
    yh = np.round(y_pred)
    train_acc.append(accuracy(yh, y))
    loss_train.append(loss(y_pred, y, lamda, w)/num_train)
    
    y_test_pred = get_prob(x_test, w, b)
    yh_test = np.round(y_test_pred)
    test_acc.append(accuracy(yh_test, y_test))
    loss_validation.append(loss(y_test_pred, y_test, lamda, w)/num_dev)

 6.训练效果

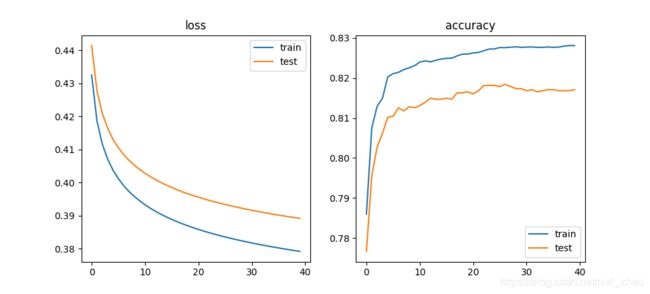
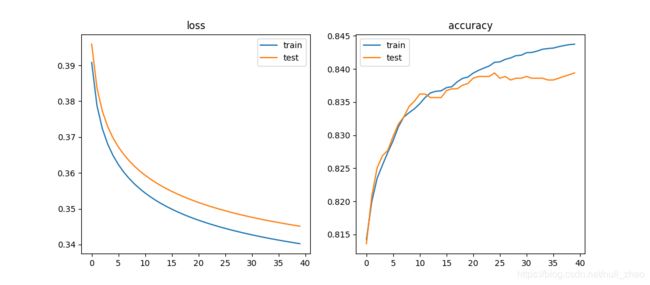
在本实验中使用均值和标准差的归一方法训练的模型似乎性能会比最小最大值归一方法好很多，暂不清楚原因。

• 使用min,max归一

• 使用mean,std归一