激活函数 activation function
文章目录
-
- 激活函数 activation function
- Sigmoid
- Sigmoid 反向传播
- Tanh
- ReLU
- Dead ReLU Problem 产生的原因
激活函数 activation function
激活函数的角色是引入非线性(non-linearity),否则不管网络有多深,整个网络都可以直接替换为一个相应的仿射变换(affine transformation),即线性变换(linear transformation),比如旋转、伸缩、偏斜、平移(translation)。
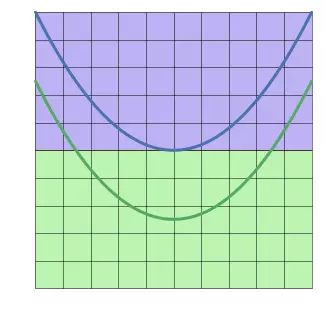
例如,在二维特征空间上,蓝线表示负面情形 y = 0 y=0 y=0,绿线表示正面情形 y = 1 y=1 y=1:
如果不使用激活函数,神经网络最好的分类效果如下:
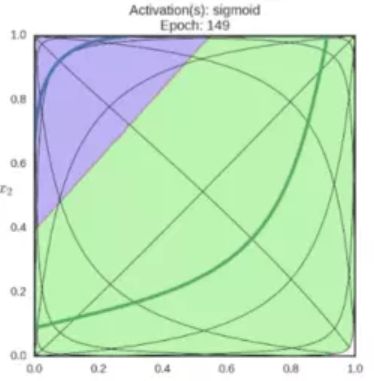
在仿射变换的结果上应用激活函数,可以对特征空间进行扭曲翻转,最后得到一条线性可分的边界。运转中的sigmoid激活函数:
在同一个网络中混合使用不同类型的神经元是非常少见的,虽然没有什么根本性问题来禁止这样做。
Sigmoid
Sigmoid 激活函数:
f ( w , x ) = 1 1 + e − ( w 0 x 0 + w 1 x 1 + w 2 ) \displaystyle f(w,x)=\frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}} f(w,x)=1+e−(w0x0+w1x1+w2)1
-
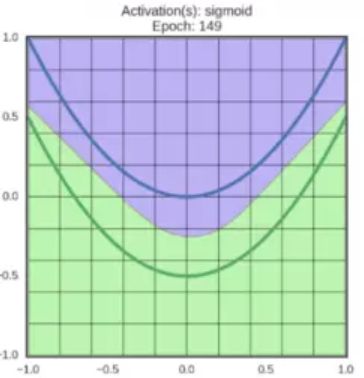
函数图像如上图所示,它将输入的值“挤压”到 [ 0 , 1 ] [0,1] [0,1] 范围内,很大的负数变成0,很大的正数变成1。
-
在历史上,Sigmoid 函数非常常用,这是因为它对于神经元的激活频率有良好的解释:从完全不激活(0)到在求和后的最大频率处的完全饱和(saturated)的激活(1)。
现在 Sigmoid 函数已经很少使用了,这是因为它有两个主要缺点:
-
Sigmoid函数饱和使梯度消失:
Sigmoid 神经元有一个不好的特性,就是当神经元的激活在接近 0 或1 处时会饱和:在这些区域,梯度几乎为0。在深层网络的链式求导过程中,如果局部梯度非常小,那么相乘的结果也会接近零,导致梯度消失。
-
Sigmoid 函数的输出不是零中心的:
这会导致后面层中的神经元得到的数据也不是零中心的,这一情况将影响梯度下降的速度,因为如果输入神经元的数据总是正数(比如在 f = w T x + b f=w^Tx+b f=wTx+b 中每个元素都 x > 0 x>0 x>0),那么权重的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数。这将会导致梯度下降权重更新时出现 Z Z Z 字型的下降。
然而,由于整个批量的数据的梯度被加起来后,对于权重的最终更新将会有不同的正负,这样就从一定程度上减轻了这个问题。因此,该问题相对于上面的神经元饱和问题来说只是个小麻烦,没有那么严重。
激活变换效果:
Sigmoid 反向传播
Sigmoid 激活函数:
f ( w , x ) = 1 1 + e − ( w 0 x 0 + w 1 x 1 + w 2 ) \displaystyle f(w,x)=\frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}} f(w,x)=1+e−(w0x0+w1x1+w2)1
链式求导:
f ( x ) = 1 x → d f d x = − 1 / x 2 \displaystyle f(x)=\frac{1}{x} \to \frac{df}{dx}=-1/x^2 f(x)=x1→dxdf=−1/x2
f c ( x ) = c + x → d f d x = 1 f ( x ) = e x → d f d x = e x \displaystyle f_c(x)=c+x \to \frac{df}{dx}=1\displaystyle f(x)=e^x \to \frac{df}{dx}=e^x fc(x)=c+x→dxdf=1f(x)=ex→dxdf=ex
f a ( x ) = a x → d f d x = a \displaystyle f_a(x)=ax \to \frac{df}{dx}=a fa(x)=ax→dxdf=a
即:
σ ( x ) = 1 1 + e − x \displaystyle\sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
→ d σ ( x ) d x = e − x ( 1 + e − x ) 2 \displaystyle\to\frac{d\sigma(x)}{dx}=\frac{e^{-x}}{(1+e^{-x})^2} →dxdσ(x)=(1+e−x)2e−x
= ( 1 + e − x − 1 1 + e − x ) ( 1 1 + e − x ) =(\frac{1+e^{-x}-1}{1+e^{-x}})(\frac{1}{1+e^{-x}}) =(1+e−x1+e−x−1)(1+e−x1)
= ( ( 1 + e − x 1 + e − x ) − ( 1 1 + e − x ) ) ( 1 1 + e − x ) =((\frac{1+e^{-x}}{1+e^{-x}})-(\frac{1}{1+e^{-x}}))(\frac{1}{1+e^{-x}}) =((1+e−x1+e−x)−(1+e−x1))(1+e−x1)
= ( 1 − σ ( x ) ) σ ( x ) =(1-\sigma(x))\sigma(x) =(1−σ(x))σ(x)
在分子上先加 1 后减 1 来简化求导过程:
计算线路:
根据上面的公式,局部梯度为 ( 1 − 0.73 ) ∗ 0.73 = 0.2 (1-0.73)*0.73~=0.2 (1−0.73)∗0.73 =0.2
w = [2,-3,-3] # 假设一些随机数据和权重
x = [-1, -2]
# 前向传播
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid函数
# 对神经元反向传播
ddot = (1 - f) * f # 点积变量的梯度, 使用sigmoid函数求导
dx = [w[0] * ddot, w[1] * ddot] # 回传到x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 回传到w
# 完成!得到输入的梯度
Tanh
-
tanh 神经元是一个简单放大平移后的 Sigmoid 神经元。
-
tanh 公式:
t a n h ( x ) = 2 s i g m o i d ( 2 x ) − 1 tanh(x)=2sigmoid(2x)-1 tanh(x)=2sigmoid(2x)−1
t a n h ( x ) = e x − e − x e x + e − x tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} tanh(x)=ex+e−xex−e−x
-
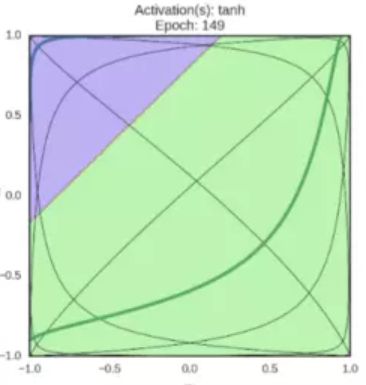
图像如上图所示。它将实数值压缩到 [ − 1 , 1 ] [-1,1] [−1,1] 之间。和 Sigmoid 神经元一样,它也存在饱和问题,但是和 Sigmoid 神经元不同的是,它的输出是零中心的。因此,在实际操作中,tanh 非线性函数比 Sigmoid 非线性函数更受欢迎。
激活变换效果:
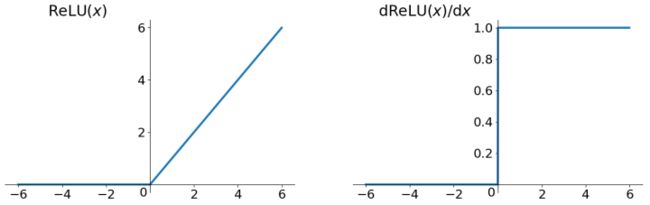
ReLU
ReLU(校正线性单元:Rectified Linear Unit)激活函数,当 x = 0 x=0 x=0 时函数值为0。当 x > 0 x>0 x>0 函数的斜率为 1。使用 ReLU 可以加快收敛速度。
- 在近些年 ReLU变得非常流行,它的函数公式是:
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
- ReLU 函数其实就是一个取最大值函数,它并不是全区间可导的,但是可以取 sub-gradient,如上图所示。
ReLU的优点:
-
sigmoid 和 tanh 神经元含有指数运算等耗费计算资源的操作,而 ReLU 可以简单地通过对一个矩阵进行阈值计算得到。
-
相较于 sigmoid 和 tanh 函数,ReLU 对于随机梯度下降的收敛有巨大的加速作用。
ReLU的缺点:
-
ReLU 的输出不是零中心的。
-
Dead ReLU Problem:ReLU 不适合大梯度传播,因为在前层参数更新以后,ReLU 的神经元有可能再也不能被激活,导致梯度永远都是零。通过合理设置学习速率,这种情况的发生概率会降低。
激活变换效果:
Dead ReLU Problem 产生的原因
假设有一个神经网络的输入 W W W 遵循某种分布,对于一组固定的样本, W W W 的分布也就是 ReLU 的输入的分布,假设 ReLU 输入是一个低方差中心在 + 0.1 +0.1 +0.1 的高斯分布。
在这个场景下:
-
大多数 ReLU 的输入是正数
-
大多数输入经过 ReLU 函数能得到一个正值(ReLU is open)
-
大多数输入能够反向传播通过 ReLU 得到一个梯度
-
ReLU 的输入 W W W 一般都能通过反向传播得到更新
现在,假设在随机反向传播的过程中,有一个巨大的梯度经过 ReLU,由于 ReLU是打开的,将会有一个巨大的梯度通过反向传播传给输入 W W W 。这会引起输入 W W W 巨大的变化,也就是说输入 W W W 的分布会发生变化,假设输入 W W W 的分布现在变成了一个低方差的,中心在 − 0.1 -0.1 −0.1 高斯分布。
在这个场景下:
-
大多数 ReLU 的输入是负数
-
大多数输入经过 ReLU 函数会得到 0 值(ReLU is close)
-
大多数输入通过 ReLU 反向传播,得到一个梯度也是 0
-
ReLU 的输入 W W W 大多数都无法通过反向传播得到更新了
发生了什么?只是ReLU函数的输入的分布函数发生了很小的改变( − 0.2 -0.2 −0.2 的改变),导致了ReLU函数行为质的改变。越过了 0 这个边界,ReLU 函数几乎永久的关闭了。更重要的是ReLU函数一旦关闭,参数 W W W 就得不到更新,这就是所谓的 dying ReLU,过高的学习速率可能是这里的罪魁祸首。