GAMES101 Assignment 3
前言
通过阅读实验提供的代码框架,可以加深对渲染管线的理解。assignment1,2我并没有做,我们课程图形学本来有实验计划,然而老师专门让我们做GAMES101的这个实验,其意义可见一斑。
阅读过程中遇到许多困难,看了许多资料以及平台的论坛,很受启发,重要资源附在文末。
实验目的
实验内容


第②点讲错了,一开始把这个点错理解为视点,它就是模型的顶点,后面用来插值得到渲染点的shadingcoords.


细心的朋友会发现一些问题。code 中用投影后的点计算重心坐标,通过几步运算得到插值点的深度(z坐标),然后依次插值得到颜色、法线、纹理坐标以及 shadingcoords.
首先,shadingcoords是什么?
它是要渲染点(在 shader 中就是红色圈出来的点)在相机坐标系下的坐标,通过仅经过mv变换(代码中有体现)的三角形顶点插值得到。

为什么深度的插值计算和其他属性不同?
投影前后,重心坐标会发生变化,进行属性插值按理使用投影前的重心。那么我们如何计算投影前的重心?
透视矫正插值
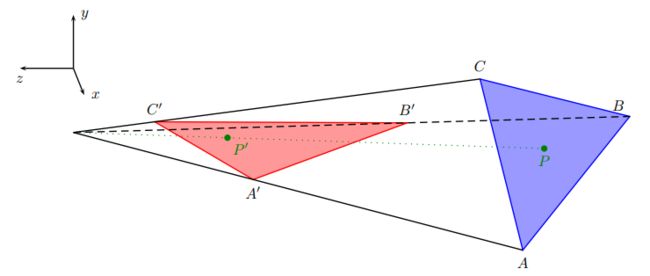
对蓝色三角形进行齐次变换 M M M得到红色三角形,设 K = A , B , C , P K={A,B,C,P} K=A,B,C,P,有
[ K ′ w k w k ] = M [ K 1 ] \begin{bmatrix} K'w_k \\ w_k \end{bmatrix}=M \begin{bmatrix} K \\ 1 \end{bmatrix} [K′wkwk]=M[K1]
注意到在进行齐次除法时保留了 w k w_k wk. 设点 P 变换前后重心坐标为 ( α , β , γ ) (\alpha,\beta,\gamma) (α,β,γ)以及 ( α ′ , β ′ , γ ′ ) (\alpha',\beta',\gamma') (α′,β′,γ′),满足
P = α A + β B + γ C P ′ = α ′ A ′ + β ′ B ′ + γ ′ C ′ P=\alpha A+\beta B+\gamma C \\ P'=\alpha' A'+\beta' B'+\gamma' C' P=αA+βB+γCP′=α′A′+β′B′+γ′C′
利用 α + β + γ = 1 \alpha+\beta+\gamma=1 α+β+γ=1构建等式,建立变换前后重心坐标的关系:
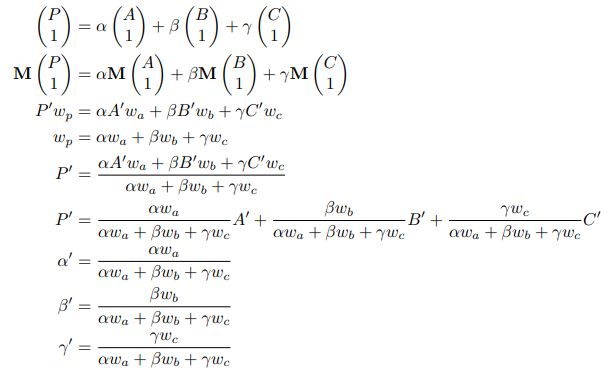
但是现在是已知投影后的重心坐标,因此应该用 α ′ , β ′ , γ ′ \alpha',\beta',\gamma' α′,β′,γ′表示 α \alpha α,已知 α ′ = α w a k \alpha'=\alpha w_ak α′=αwak,尝试将 k k k用 α ′ , β ′ , γ ′ \alpha',\beta',\gamma' α′,β′,γ′表达即可:

Z变量 对应的正是公式中 k!因此深度是通过透视矫正插值精确计算的,而其他属性是通过投影后重心坐标简单近似插值计算的。
看这个回帖:

帖子:https://games-cn.org/forums/topic/zuoye3-interpolated_shadingcoords/
截图材料:https://www.cs.ucr.edu/~craigs/courses/2018-fall-cs-130/lectures/perspective-correct-interpolation.pdf
auto tup = computeBarycentric2D((float)x + 0.5, (float)y + 0.5, t.v);
float alpha, beta, gamma; // 利用重心坐标进行属性插值
std::tie(alpha, beta, gamma) = tup;
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z; // 深度
if (zp < depth_buf[get_index(x, y)])
{
// 近似插值
auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);
auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1).normalized();
auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);
auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);
实验结果
More
山东大学图形学课程实验代码获取:Here


