纸上谈兵——机器学习基本知识

机器学习尤其是深度学习激起了人们的空前热情，原本从事后台工程的人们也按捺不住想了解机器学习的原理，一探其中神奇。本文是我的一些总结，希望给初入此行的人们介绍一点入门概念。

初识机器学习，你是否有很多问号？

学习机器学习，熟悉各种模型和算法固然重要，但更重要的可能还在模型之外：训练样例不足怎么办？正负样本分布不均衡怎么办？如何在众多模型中选出合适的？如何根据任务特点调整损失函数？等等。没有一个模型能告诉你这些问题的答案，要想解决这些问题，就必须理解机器学习的基本概念和思想，这正是这篇文章的出发点。

模型算法分类，机器学习应该这么分

机器学习算法可分为监督学习、无监督学习、半监督学习和强化学习，其中应用最广泛的是监督学习，本文主要就是说它。所谓监督学习是指训练样例是有标签的，训练过程中要判断模型的输出和标签是否一致，以此来指导/监督学习过程。

机器学习的介绍，解析你眼中的“上帝函数”。

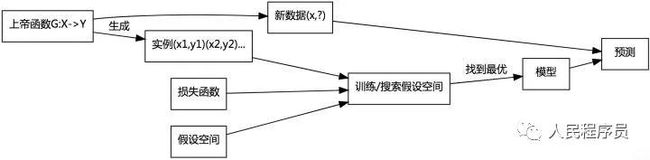
1、机器学习流程介绍

先对机器学习的流程进行下总结。

图1 机器学习的流程

2、“上帝”能从X得到Y

对于机器要学习的任务，想象有一个“上帝函数”G: X→Y或“上帝分布”G(Y|X)，它能准确无误地知道对于每个输入x应该产生的输出y。问题是我们没有办法得到这个函数，但我们能观察到它产生的一系列样例数据(x1,y1), (x2,y2), … (xn, yn)，所以很自然的想法就是通过大量样例去估计G。

3、模型需要“假设空间”

为了估计G，必须先假设它为某一种函数比如决策树或神经网络，也可能假设它服从某种概率分布如logistic分布。总之一定需要有假设才能进一步学习。每一种假设形式包含很多不同的具体函数或分布，比如n(n>0)阶多项式包含无数可能的函数。如果用机器学习的术语表述，所假设的函数形式（概率分布）就是常说的模型，模型所能包含的所有不同函数（分布）组成了“假设空间”。对于某种模型，假设空间就是一组参数表示的函数族（概率分布），例如若模型为y = ax + b，它的假设空间就由参数a，b定义的一阶多项式函数族，表示了二维空间的所有直线。

4、至关重要的“损失函数”

假设空间包含很多假设，我们自然希望找到最合适的那个假设，而衡量合不合适的标准就是损失函数，它度量了模型的预测值和真实值之间的差别，通常越小说明模型越好。假设空间通常包含无限多个函数，所以训练过程通常也非常耗时，为了加速训练使误差尽快收敛，人们研究出了各种训练算法，如梯度下降，反射传播等。所以，机器学习的训练过程就是由损失函数引导着在假设空间中用特定算法不断搜索，直到找到满足损失函数的那个函数。可见所谓的“智能”、“学习”不过是“暴力搜索”假设空间，因为只要算力足够强到能把无限大的假设空间搜索一遍，自然就能找到最优的模型，这也是机器学习被人诟病的地方，哪怕确实有聪明的算法能加快搜索。

5、实测的准确性才是王道

在得到期望的假设后，就能将它用于预测了。预测才是机器学习的最终目的，这一点很重要，哪怕在训练时误差为0也没有用，必须在预测时表现好才是成功。
前面提到，机器学习的训练过程就是由损失函数引导着在假设空间中用特定算法不断搜索，直到找到满足损失函数的那个函数。可见当模型，损失函数和算法确定后，要怎么学习也就确定了，所以这就是机器学习的三要素。

机器学习小贴士之——模型

由前文知道模型就是一个函数族，这可以用数学语言表示如下：

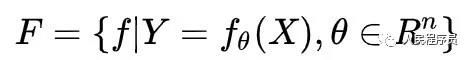
其中X，Y是随机变量，分别表示函数的输入和输出，θ为n维的参数向量。模型也可能是概率分布族：

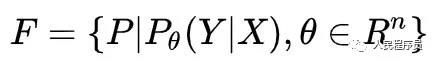
其中P表示概率分布。

机器学习小贴士之——损失函数

对于输入X，模型产生输出f(X)，损失函数L度量预测值f(X)与真实值Y的差别程度，常用的有这些：
a) 0-1损失函数

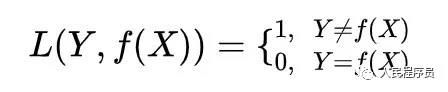
b) 平方损失函数

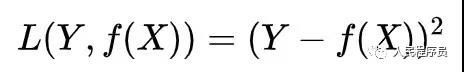
c) 交叉熵

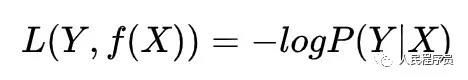
也可以表示为：

其中，(x,y)是一个样例。这两个表达是等价的。上面的交叉熵是用于二分类的，可以很容易推广到多分类的情况。看面相就知道交叉熵很不简单，值得好好研究。
损失函数定义了单个样例的损失，一个训练样例集合(x1,y1),(x2,y2),…(xN,yN)上的平均损失定义如下：

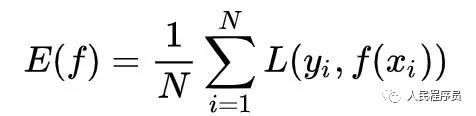
称为经验损失。实际训练时以最小化E(f)为目标。

机器学习小贴士之——算法

不同的模型通常有不同的训练算法，如牛顿法，梯度下降法，SMO算法及反射传播，现在只要理解这些算法都是用于搜索假设空间就可以了，在遇到具体模型时再学习也不晚，这里不再展开。

看完这三要素，应该对机器学习有了一些感性认识了，虽然看似简单，但实际中每一步都是陷阱。我能想到的，与样例相关的问题有：独立同分布，样例不足，样例不均衡；与模型有关的有：特征工程，过拟合与欠拟合。

机器学习小贴士之——独立同分布

训练样例和预测用的新数据必须是独立同分布的。
先看同分布。机器学习的训练过程是在学习训练样例集上的统计规律，所以如果新数据来自不同的概率分布，那预测结果不可能准确。这让我想起多年前的一个项目，当时大家从某点评抓取数据训练一个分类器，然后用它对美食类微博进行分类。两者虽然内容相似但样例分布肯定大不相同，效果不可能好。再比如用户时长预估问题，人们可能在通勤时或周末观看时间较长，而上班时间观看时间较短，所以如果全都用来自前一时间段的训练样例训练模型，并预测后一时间段的观看时长，那必然是失败的。
再说独立。样例其实不太可能独立，比如用户点击的文章A后很可能点击相关或相似的文章B，而如果用户先看到B可能就不点击它的。这在新闻场景下应该比较明显，某个很久不出现的明星出了大新闻，用户很可能点击，然后再看看ta之前的相关文章；但直接推荐之前的文章，用户可能并没有兴趣。但实际中是将样例当成相互独立处理的，如若不然学习过程就太复杂了。
再回到推荐系统工程上，有人证明模型更新较快能使推荐结果更准确，我想根源可能也在于这一点，就是老模型是在老概率分布、老样例上的训练结果，而生成新数据的概率分布可能已经不同。

机器学习小贴士之——样例不足

样例不足是相对模型的输入维度而言的，模型越复杂一般输入维度越多，也就是常说的特征数越多，这时为了成功训练模型就需要越多的样例。对参数量巨大的深度学习尤其如此。
解决样例不足问题最直接的办法就是降低模型复杂度，从而减少需要的训练样例数量。另一方面，样例集合可以看成是对“上帝函数”的采样，所以如果能在样例集合上等概率地插值采样，就能既不破坏训练样例的概率分布，又得到更多的可用样例。在将深度学习应用到图像领域时，还可以将图像做反转，裁剪从而得到更多样例。此外，据说迁移学习可以很好地解决这个问题，有待学习。
需要大量训练样例这一点也是机器学习被诟病的地方。机器“看”了海量的图片，最终还是不能完全准确地认识狗或猫，而只要给小孩看很少几张小鸟的图片，即使再给ta一张很不相同的小鸟图片，ta也能正确地认出来。
最后，互联网行业的人见过很多数据，对“样例不足”可能没有认识。一个样例不足的例子是医疗数据，各大医院应该还不至于共享自家的医疗数据，这是所谓的“智慧医疗”必须要面对的。

机器学习小贴士之——正负样例不均衡

这是分类学习中遇到的问题，正负样例分别表示不同的类别。不均衡一般是负样例不足，如银行交易中的金融欺诈案例相对正常交易数量少很多。这和样例不足有点相似，只不过是一方的样例不足，所以很自然地可以考虑对不足的一方重新采样以获得更多的数据。
再考虑金融欺诈问题，假设样例集合大小为1万，其中只有一个为欺诈案例。考虑上面的经验风险函数，这里即使分类器将所有样例都分类为正例，它的正确率仍能高达99.99%。这肯定不合理。一种做法是将损失函数乘以一个系数，这个系数对负样例非常大，对正样例比较小，这样经验风险中正负样例造成的损失的比例就能相当，从而让它不能“忽视”负样例。
根据不同场景选择或改造损失函数是一项重要技能，也是判断是否熟悉机器学习的一个方面。

机器学习小贴士之——特征工程

模型都是公开的，但各家用起来效果各不相同，很大一部分原因应该在于“特征工程”。外行看算法工程师“高大上”，但他们大部分时间应该都是在做“特征工程”，与数据打交道：观察，清洗，转换，组合等等。这是因为发掘出好的特征往往事半功倍，能让模型效果获得极大提升；另一方向，“上帝函数”产生的输入数据一般不适合直接送给模型用，而是要先经过一些处理。前者应该不难理解，后者中比较典型的有one-hot编码，对数据进行多维统计等。
深度学习及word2vec的出现似乎改变了传统的“特征工程“，算法工程师仍然在着力发掘新特征，但现在对特征的变换更喜欢使用w2v，i2v或graph embedding等操作。

机器学习小贴士之——过拟合与欠拟合

可以这样讲，不理解过拟合和欠拟合就不能说理解机器学习！它们的本质是分析误差出在哪里。
前文提到要学习“上帝函数”G就必须先假设它是某个函数f，但大多数时候f不可能和G相同，即使我们真的知道G”真容”，但由于数据噪声的存在，训练得到的模型和G也不会相同，所以f和G之间天然地就有误差，这被称为“偏差”。偏差使模型不能完全地拟合训练集中的样例，不能完全地获得数据中的统计规律，这就是“欠拟合”。
另一方面，为了更好地拟合训练样例，人们将模型变得越来越复杂，对应的假设空间也越大。模型越复杂就越是能抓住数据中的”特征“，哪怕这些特征实际上只是噪声，结果稍微不同的训练集就导致差别很大的模型，也就是模型自身随数据集变动剧烈，这个度量被称为”方差“。方差大的模型，意味着模型的输出很不稳定，现象就是模型的训练误差非常小但预测错误率很高，这就是“过拟合”。

欠拟合和过拟合应对之策

机器学习必须在欠拟合和过拟合之间找到一个平衡，让模型既能尽量多地获取数据中的特征，又不至于被噪声干扰太重。这就像相互矛盾的两个方向，一方面要不断增加模型复杂度，让它学到更多规律特征，另一方面又要相当地克制以免模型陷入噪声不能自拔。
实际中对经验风险进行了改造，加了上模型复杂度考量：

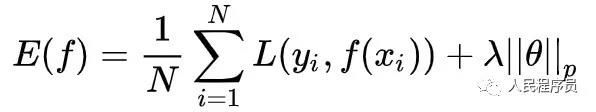
式中λ为非负实数，为模型参数，为1或2，分别表示一阶或二阶范数。这样，当模型拟合训练集效果越好，等式前一项越来越小；但同时模型越复杂参数越多，这又使得后一项越来越大。训练过程就在这种”纠结“"钳制"达到一种平衡。
除此之外，数据集一般会分为”训练集“，”验证集“和”测试集“。学习过程中，在训练集上训练模型，学完一次后在验证集上验证学习效果并不断改进；待在验证集上得到满意效果后再在测试集上测试模型最终效果。这里验证集就能起到防止过拟合的目的，因为一旦发现训练误差很小但验证误差很大，就能断定是发生了过拟合，这时就要降低模型复杂度。
对于不同模型还有不同的防止过拟合策略，如树模型的剪枝，减少树的深度（或称高度），学习提前结束迭代等。对于深度学习还有很神奇的dropout，google还为它申请了专利。它的思路是在反射传播时随机地放弃更新部分节点。
总之，要让机器学习，就必然要面对并解决过拟合问题。

参考资料：

统计学习方法，李航，第一版
机器学习，Tom Mitchell，好像没有第二版
https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff

作者：卢新来，已获转载授权

想获取更多内容，请关注海数据实验室公众号。

本期分享到这里，我们会每天更新内容，咱们下期再见，期待您的再次光临。有什么建议，比如想了解的知识、内容中的问题、想要的资料、下次分享的内容、学习遇到的问题等，请在下方留言。如果喜欢请关注。社群推荐：

更多有关数据分析的精彩内容欢迎加入海数据在线数据分析交流群，有什么想法或者疑问都可在里面提出，与同行零距离交流，共同成长进步，请识别下面二维码加火星小海马微信，邀你进群。