Python零基础速成班-第15讲-Python for Numpy 基础知识及应用
Python零基础速成班-第15讲-Python for Numpy 基础知识及应用
学习目标
- Numpy 基础知识及应用
友情提示:将下文中代码拷贝到JupyterNotebook中直接执行即可,部分代码需要连续执行。
1、Numpy 基础知识及应用
1.1 Numpy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。
1.Numpy 最重要的一个特点是其 N 维数组对象 ndarray,它是一系列同类型数据的集合,以 0 下标为开始进行集合中元素的索引。
2.ndarray 对象是用于存放同类型元素的多维数组。
3.ndarray 中的每个元素在内存中都有相同存储大小的区域。
4.ndarray 内部由以下内容组成:
- 一个指向数据(内存或内存映射文件中的一块数据)的指针。
- 数据类型或 dtype,描述在数组中的固定大小值的格子。
- 一个表示数组形状(shape)的元组,表示各维度大小的元组。
- 一个跨度元组(stride),其中的整数指的是为了前进到当前维度下一个元素需要"跨过"的字节数。
Numpy 英文官方网站及文档:https://numpy.org/doc/stable/user/index.html
Numpy 中文参考文档:https://www.runoob.com/numpy/numpy-ndarray-object.html
接下来可以通过以下实例帮助我们更好的理解:
import numpy as np
a = np.array([1,2,3])
print (a)
[1 2 3]
多于一个维度
import numpy as np
a = np.array([[1, 2], [3, 4]])
print (a)
[[1 2]
[3 4]]
最小维度,ndmin = 2 表示二维数组
import numpy as np
a = np.array([1, 2, 3, 4, 5], ndmin = 2)
print (a)
[[1 2 3 4 5]]
dtype 参数,complex为复数
import numpy as np
a = np.array([1, 2, 3], dtype = complex)
print (a)
1.2 Numpy 数组属性
Numpy 数组的维数称为秩(rank),秩就是轴的数量,即数组的维度,一维数组的秩为 1,二维数组的秩为 2,以此类推。
在 Numpy中,每一个线性的数组称为是一个轴(axis),也就是维度(dimensions)。比如说,二维数组相当于是两个一维数组,其中第一个一维数组中每个元素又是一个一维数组。所以一维数组就是 NumPy 中的轴(axis),第一个轴相当于是底层数组,第二个轴是底层数组里的数组。而轴的数量——秩,就是数组的维数。
很多时候可以声明 axis。axis=0,表示沿着第 0 轴进行操作,即对每一列进行操作;axis=1,表示沿着第1轴进行操作,即对每一行进行操作。
Numpy 的数组中比较重要 ndarray 对象属性有:
| 属性 | 说明 |
|---|---|
| ndarray.ndim | 秩,即轴的数量或维度的数量 |
| ndarray.shape | 数组的维度,对于矩阵,n 行 m 列 |
| ndarray.size | 数组元素的总个数,相当于 .shape 中 n*m 的值 |
| ndarray.dtype | ndarray 对象的元素类型 |
| ndarray.itemsize | ndarray 对象中每个元素的大小,类型长度除以8。例如,float64类型大小为8(=64/8),complex32类型大小为4(=32/8) |
| ndarray.flags | ndarray 对象的内存信息 |
| ndarray.real | ndarray元素的实部 |
| ndarray.imag | ndarray 元素的虚部 |
| ndarray.data | 包含实际数组元素的缓冲区,由于一般通过数组的索引获取元素,所以通常不需要使用这个属性。 |
import numpy as np
a = np.arange(15).reshape(3, 5)
print(a)
print("形状:",a.shape)
print("维度:",a.ndim)
print("元素类型:",a.dtype.name)
print("元素类型长度:",a.itemsize)
print("元素个数为:",a.size)
print("数组类型:",type(a))
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
形状: (3, 5)
维度: 2
元素类型: int32
元素类型长度: 4
元素个数为: 15
数组类型:
1.3 Numpy 数组创建
1.3.1 通过np.array()创建
[2, 3, 4]元素类型为int32;[1, 3.5, 5.1]有小数点,所以元素类型为float64。
import numpy as np
a = np.array([2, 3, 4])
print(a)
print("元素类型:",a.dtype)
b = np.array([1, 3.5, 5.1])
print("元素类型:",b.dtype)
[2 3 4]
元素类型: int32
元素类型: float64
import numpy as np
a = np.array([[1.5, 2, 3], [4, 5, 6]])
b = np.array([(1.5, 2, 3), (4, 5, 6)])
print(a)
print(b)
[[1.5 2. 3. ]
[4. 5. 6. ]]
[[1.5 2. 3. ]
[4. 5. 6. ]]
import numpy as np
c = np.array([[1, 2], [3, 4]], dtype=complex)# 复数
print(c)
[[1.+0.j 2.+0.j]
[3.+0.j 4.+0.j]]
1.3.2 通过np.zeros创建,使用数字0填充数组
import numpy as np
print(np.zeros(3))
print(np.zeros([3, 4]))
[0. 0. 0.]
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
1.3.3 通过np.ones创建,使用数字1填充数组
import numpy as np
np.ones((2, 3, 4), dtype=np.int16)
array([[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]],
[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]], dtype=int16)
1.3.4 np.empty()创建一个数组,其初始内容是随机的,并且取决于内存的状态
import numpy as np
np.empty((2, 3))
array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])
1.3.5 创建数字序列,Numpy提供了arange函数,类似于Python的内置范围,返回一个数组。
语法:np.arange(start, end, step) 从start开始到end结束不包含end,step为步长。
import numpy as np
print(np.arange(10, 30, 5))
print(np.arange(0, 2, 0.3))
[10 15 20 25]
[0. 0.3 0.6 0.9 1.2 1.5 1.8]
1.3.6 通过np.linspace()创建一个切片数组,即等差数列
import numpy as np
from numpy import pi
print(np.linspace(0, 2, 9)) # 将0-2切分为9组
x = np.linspace(0, 2 * pi, 10)
print(x)
[0. 0.25 0.5 0.75 1. 1.25 1.5 1.75 2. ]
[0. 0.6981317 1.3962634 2.0943951 2.7925268 3.4906585
4.1887902 4.88692191 5.58505361 6.28318531]
1.3.7 打印数组
一般来说满足最后一个轴从左向右打印,从上到下打印,每一部分与下一部分之间用空行隔开。
import numpy as np
a = np.arange(6) # 1d array
print("一维数组:\n",a)
b = np.arange(12).reshape(4, 3) # 2d array
print("二维数组:\n",b)
c = np.arange(1,25).reshape(2, 3, 4) # 3d array
print("三维数组:\n",c)
一维数组:
[0 1 2 3 4 5]
二维数组:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
三维数组:
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
如果数组太大而无法打印,Numpy自动跳过阵列的中心部分,只打印角点。
import numpy as np
print(np.arange(10000))
[ 0 1 2 ... 9997 9998 9999]
import numpy as np
print(np.arange(10000).reshape(100, 100))
[[ 0 1 2 ... 97 98 99]
[ 100 101 102 ... 197 198 199]
[ 200 201 202 ... 297 298 299]
...
[9700 9701 9702 ... 9797 9798 9799]
[9800 9801 9802 ... 9897 9898 9899]
[9900 9901 9902 ... 9997 9998 9999]]
1.4 Numpy 数组基本操作
1.4.1 数学函数和算术运算
import numpy as np
a = np.array([20, 30, 40, 50])
b = np.arange(4)
print("a数组:",a)
print("b数组:",b)
print("两个数组相减:",a-b)
print("b数组求2次方:",b**2)
print("sin(a)乘以10:",10 * np.sin(a))
print("a数组是不是都小于35:",a < 35)
a数组: [20 30 40 50]
b数组: [0 1 2 3]
两个数组相减: [20 29 38 47]
b数组求2次方: [0 1 4 9]
sin(a)乘以10: [ 9.12945251 -9.88031624 7.4511316 -2.62374854]
a数组是不是都小于35: [ True True False False]
1.4.2 二维数组元素相乘和矩阵相乘
A * B 表示元素相乘,即按位相乘。
A @ B 表示矩阵相乘,当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以矩阵相乘,即行 * 列后相加,矩阵相乘的另一种写法是A.dot(B)。
[1*2 + 1*3] [1*0 + 1*4]
[0*2 + 1*3] [0*0 + 1*4]
import numpy as np
A = np.array([[1, 1],
[0, 1]])
B = np.array([[2, 0],
[3, 4]])
print("A*B:\n",A * B) # elementwise product 元素相乘
print("A@B:\n",A @ B) # matrix product 矩阵相乘
print("A.dot(B):\n",A.dot(B)) # another matrix product
A*B:
[[2 0]
[0 4]]
A@B:
[[5 4]
[3 4]]
A.dot(B):
[[5 4]
[3 4]]
1.4.3 赋值操作及随机数生成器
有些操作(如+=和*=)会就地修改现有数组,而不是创建新数组。
np.random.default_rng(1) 表示创建默认随机数生成器的实例,从0到1。
import numpy as np
rg = np.random.default_rng(1) # 随机数实例,从0到1
a = np.ones((2, 3), dtype=int)
print("a:\n",a)
b = rg.random((2, 3))
print("b:\n",b)
a *= 3
print("a *= 3:\n",a)
b += a
print("b += a:\n",b)
a += b # a += b 报错,因为b不会自动转换为整数类型,存在精度差
a:
[[1 1 1]
[1 1 1]]
b:
[[0.51182162 0.9504637 0.14415961]
[0.94864945 0.31183145 0.42332645]]
a *= 3:
[[3 3 3]
[3 3 3]]
b += a:
[[3.51182162 3.9504637 3.14415961]
[3.94864945 3.31183145 3.42332645]]
---------------------------------------------------------------------------
UFuncTypeError Traceback (most recent call last)
~\AppData\Local\Temp/ipykernel_4336/1550870564.py in
12 print("b += a:\n",b)
13
---> 14 a += b # a += b 报错,因为b不会自动转换为整数类型,存在精度差
UFuncTypeError: Cannot cast ufunc 'add' output from dtype('float64') to dtype('int32') with casting rule 'same_kind'
1.4.4 向上转换行为
使用不同类型的阵列时,结果数组的类型对应于更一般或更精确的类型(一种称为向上投射的行为)。
如下例,a元素类型为整型,b元素类型为浮点,c =a+b,则c元素类型为浮点。
import numpy as np
a = np.ones(3, dtype=np.int32)
b = np.linspace(0, pi, 3)
print("a数组为:\n",a)
print("b数组为:\n",b)
c = a + b
print("c数组为:\n",c)
print("c元素类型:",c.dtype)
d = np.exp(c * 1j)#exp是高等数学里以自然常数e为底的指数函数
print(d)
print("d元素类型:",d.dtype)
a数组为:
[1 1 1]
b数组为:
[0. 1.57079633 3.14159265]
c数组为:
[1. 2.57079633 4.14159265]
c元素类型: float64
[ 0.54030231+0.84147098j -0.84147098+0.54030231j -0.54030231-0.84147098j]
d元素类型: complex128
1.5 Numpy 统计函数
Numpy 提供了很多统计函数,用于从数组中查找最小元素,最大元素,百分位标准差和方差等。
import numpy as np
a = rg.random((2, 3))
print(a)
print(a.sum())
print(a.min())
print(a.max())
[[0.96165719 0.72478994 0.54122686]
[0.2768912 0.16065201 0.96992541]]
3.635142616021385
0.16065200877512686
0.9699254132161326
多维度统计,axis=0 表示每列(跨行)统计,axis=1 表示每行(跨列)统计
import numpy as np
b = np.arange(12).reshape(3, 4)
print("b数组为:\n",b)
print("b数组每列求和:\n",b.sum(axis=0))
print("b数组每行求和:\n",b.sum(axis=1))
print("b数组每行最小值:\n",b.min(axis=1))
print("b数组每行累加:\n",b.cumsum(axis=1))
b数组为:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
b数组每列求和:
[12 15 18 21]
b数组每行求和:
[ 6 22 38]
b数组每行最小值:
[0 4 8]
b数组每行累加:
[[ 0 1 3 6]
[ 4 9 15 22]
[ 8 17 27 38]]
1.6 Numpy 通用函数
Numpy提供了熟悉的数学函数,如sin、cos和exp,在Numpy中,这些函数对数组进行元素操作,生成一个数组作为输出。
import numpy as np
B = np.arange(3)
print(B)
# 以自然常数e为底的指数函数
print(np.exp(B))
# 求平方根
print(np.sqrt(B))
# 两个数组相加
C = np.array([2., -1., 4.])
print(np.add(B, C))
[0 1 2]
[1. 2.71828183 7.3890561 ]
[0. 1. 1.41421356]
[2. 0. 6.]
1.7 Numpy 索引、切片和迭代
一维数组可以被索引、切片和迭代,就像Python list数组一样。
import numpy as np
a = np.arange(10)**3
print("a数组为:\n",a)
print("a数组索引2为:\n",a[2])
print("a数组切片2到5为:\n",a[2:5])
print("a数组反向排列为:\n",a[::-1])
a数组为:
[ 0 1 8 27 64 125 216 343 512 729]
a数组索引2为:
8
a数组切片2到5为:
[ 8 27 64]
a数组反向排列为:
[729 512 343 216 125 64 27 8 1 0]
针对二维数组或者三维数组的相关操作
如下例,这是一个三维数组(包含两个堆叠的二维数组)
import numpy as np
c = np.array([[[ 0, 1, 2],
[ 10, 12, 13]],
[[100, 101, 102],
[110, 112, 113]]])
print("c数组形状维度为:\n",c.shape)
print("取c数组内的第一个堆叠数组:\n",c[0, ...])
print("取c数组内两个堆叠数组的第一行:\n",c[...,0,:])
print("取c数组内两个堆叠数组内的每个数组的第三列:\n",c[..., 2])
c数组形状维度为:
(2, 2, 3)
取c数组内的第一个堆叠数组:
[[ 0 1 2]
[10 12 13]]
取c数组内两个堆叠数组的第一行:
[[ 0 1 2]
[100 101 102]]
取c数组内两个堆叠数组内的每个数组的第三列:
[[ 2 13]
[102 113]]
1.8 Numpy 形状操纵、变形
np.floor() 将数组内元素整体向下取整
import numpy as np
# 设置随机因子,随机取0-1之间取数
rg =np.random.default_rng(1)
# 取3行4列0-1随机数乘以10后 floor 向下取整
a = np.floor(10*rg.random((3, 4)))
print(a)
[[5. 9. 1. 9.]
[3. 4. 8. 4.]
[5. 0. 7. 5.]]
一些常用的形状操纵、变形相关函数:
- ravel() 返回一个展平后的一维数组。
- reshape()返回具有修改形状的数组。
- .T 返回转置的数组(转置卷积,将行列互转)。
import numpy as np
rg =np.random.default_rng(11)
# np.ceil() 将数组内元素整体向上取整
A = np.ceil(10*rg.random((3, 4)))
print("A数组为:\n",A)
print("A展平后的数组为:\n",A.ravel())
print("A变形后的数组为:\n",a.reshape(6, 2))# 变为6行2列
print("A转置后的数组为:\n",A.T)
print("A数组的维度形状为:\n",A.shape)
print("A数组转置后的维度形状为:\n",A.T.shape)
# reshape()行或者列值 = -1时,则剩下行维度自动计算
print("维度自动计算:\n",A.reshape(2,-1)) # 2行,自动计算为6列
A数组为:
[[ 2. 5. 7. 1.]
[ 2. 10. 1. 2.]
[10. 7. 4. 6.]]
A展平后的数组为:
[ 2. 5. 7. 1. 2. 10. 1. 2. 10. 7. 4. 6.]
A变形后的数组为:
[[5. 9.]
[1. 9.]
[3. 4.]
[8. 4.]
[5. 0.]
[7. 5.]]
A转置后的数组为:
[[ 2. 2. 10.]
[ 5. 10. 7.]
[ 7. 1. 4.]
[ 1. 2. 6.]]
A数组的维度形状为:
(3, 4)
A数组转置后的维度形状为:
(4, 3)
维度自动计算:
[[ 2. 5. 7. 1. 2. 10.]
[ 1. 2. 10. 7. 4. 6.]]
1.9 Numpy 唯一、重复计算
- np.unique() 返回去重后的数组。
- np.unique(设置return_index=True) 返回两个数组:去重后的数组和每个唯一元素在原数组中第一次出现的index的数组。
- np.unique(设置return_counts=True) 返回两个数组:去重后的数组和统计每个唯一元素在原数组中重复的次数。
import numpy as np
a = np.array([11, 11, 12, 13, 14, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])
print("去重后的数组:",np.unique(a))
# 返回每个唯一元素在原数组中第一次出现的index
unique_values, indices_list = np.unique(a, return_index=True)
print("第一次出现的index:",indices_list)
# 统计每个唯一元素在原数组中重复的次数
unique_values, occurrence_count = np.unique(a, return_counts=True)
print("统计重复次数:",occurrence_count)
去重后的数组: [11 12 13 14 15 16 17 18 19 20]
第一次出现的index: [ 0 2 3 4 5 6 7 12 13 14]
统计重复次数: [3 2 2 2 1 1 1 1 1 1]
二维数组去重:整体所有元素去重
import numpy as np
a_2d = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[1, 2, 3, 4]])
unique_values = np.unique(a_2d)
print(unique_values)
[ 1 2 3 4 5 6 7 8 9 10 11 12]
二维数组针对行或者列去重,可以使用axis参数,axis=0 表示每列(跨行)去重,axis=1 表示每行(跨列)去重
import numpy as np
a_2d = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[1, 2, 3, 4]])
unique_rows = np.unique(a_2d, axis=0)# 返回去除行重复后的数组
print(unique_rows)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
import numpy as np
a_2d = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[1, 2, 3, 4]])
unique_rows, index, occurrence_count = np.unique(a_2d, axis=0,return_counts=True,return_index=True)
print("二维数组行去重后的数组:\n",unique_rows)
print("每行第一次出现的index:\n",index)
print("统计行重复次数:\n",occurrence_count)
二维数组行去重后的数组:
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
每行第一次出现的index:
[0 1 2]
统计行重复次数:
[2 1 1]
1.10 Numpy 反转、排序
np.flip(数组,轴) 沿指定的轴反转数组元素的顺序,从而保留数组的形状。
import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
reversed_arr = np.flip(arr)#降序排列
print("降序排列后的一维数组: ", reversed_arr)
降序排列后的一维数组: [8 7 6 5 4 3 2 1]
二维数组反转排序,外层数组和内层数组均反转排序
import numpy as np
arr_2d = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
reversed_arr = np.flip(arr_2d)
print(reversed_arr)
[[12 11 10 9]
[ 8 7 6 5]
[ 4 3 2 1]]
加入轴axis参数,axis=0 表示按列(跨行)反转排序,axis=1 表示按行(跨列)反转排序
import numpy as np
arr_2d = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
reversed_arr_rows = np.flip(arr_2d, axis=0)
print("按列反转排序(降序): \n",reversed_arr_rows)
reversed_arr_columns = np.flip(arr_2d, axis=1)
print("按行反转排序(降序): \n",reversed_arr_columns)
按列反转排序(降序):
[[ 9 10 11 12]
[ 5 6 7 8]
[ 1 2 3 4]]
按行反转排序(降序):
[[ 4 3 2 1]
[ 8 7 6 5]
[12 11 10 9]]
1.11 Numpy 数据类型
| 名称 | 描述 |
|---|---|
| bool_ | 布尔型数据类型(True 或者 False) |
| int_ | 默认的整数类型(类似于 C 语言中的 long,int32 或 int64) |
| intc | 与 C 的 int 类型一样,一般是 int32 或 int 64 |
| intp | 用于索引的整数类型(类似于 C 的 ssize_t,一般情况下仍然是 int32 或 int64) |
| int8 | 字节(-128 to 127) |
| int16 | 整数(-32768 to 32767) |
| int32 | 整数(-2147483648 to 2147483647) |
| int64 | 整数(-9223372036854775808 to 9223372036854775807) |
| uint8 | 无符号整数(0 to 255) |
| uint16 | 无符号整数(0 to 65535) |
| uint32 | 无符号整数(0 to 4294967295) |
| uint64 | 无符号整数(0 to 18446744073709551615) |
| float_ | float64 类型的简写 |
| float16 | 半精度浮点数,包括:1 个符号位,5 个指数位,10 个尾数位 |
| float32 | 单精度浮点数,包括:1 个符号位,8 个指数位,23 个尾数位 |
| float64 | 双精度浮点数,包括:1 个符号位,11 个指数位,52 个尾数位 |
| complex_ | complex128 类型的简写,即 128 位复数 |
| complex64 | 复数,表示双 32 位浮点数(实数部分和虚数部分) |
| complex128 | 复数,表示双 64 位浮点数(实数部分和虚数部分) |
import numpy as np
dt = np.dtype(np.int32)
print(dt)
int32
创建结构化数据
如下例 age 字段,np.int8类型
import numpy as np
dt = np.dtype([('age',np.int8)])
print(dt)
[('age', 'i1')]
将数据类型应用于 ndarray 对象
import numpy as np
dt = np.dtype([('age',np.int8)])
a = np.array([(10,),(20,),(30,)], dtype = dt)
print(a)
print(a['age'])
[(10,) (20,) (30,)]
[10 20 30]
定义二维数据类型,包含name,age,marks三个字段,数据类型为S20字符串20,i1整型1,f4浮点4
将数据类型应用于二维数组
import numpy as np
student = np.dtype([('name','S20'), ('age', 'i1'), ('marks', 'f4')]) #定义一个二维数组,分别为name,age,marks
print("student数据类型为:",student)
a = np.array([('Tom', 21, 50),('jerry', 18, 75)], dtype = student)
print("a数组为:",a)
print("取a数组第一组数据:",a[0])
print("取a数组name列数据:",a['name'])
print("取a数组name列第一个数据:",a['name'][0])
print("取a数组age列数据:",a['age'])
student数据类型为: [('name', 'S20'), ('age', 'i1'), ('marks', '1.12 Numpy 广播(Broadcast)
广播(Broadcast)是 numpy 对不同形状(shape)的数组进行数值计算的方式, 对数组的算术运算通常在相应的元素上进行。
如果两个数组 a 和 b 形状相同,即满足 a.shape == b.shape,那么 a * b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同,且各维度的长度相同,如下例:
import numpy as np
a = np.array([1,2,3,4])
b = np.array([10,20,30,40])
c = a * b
print (c)
[ 10 40 90 160]
当运算中的 2 个数组的形状不同时,numpy 将自动触发广播机制,如下例:
import numpy as np
a = np.array([[ 0, 0, 0],
[10,10,10],
[20,20,20],
[30,30,30]])
b = np.array([1,2,3])
print(a + b)
[[ 1 2 3]
[11 12 13]
[21 22 23]
[31 32 33]]
广播的规则:
- 让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在前面加 1 补齐。
- 输出数组的形状是输入数组形状的各个维度上的最大值。
- 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时,这个数组能够用来计算,否则出错。
- 当输入数组的某个维度的长度为 1 时,沿着此维度运算时都用此维度上的第一组值。
2、上一讲Python零基础速成班-第14讲-Python处理Excel和Word,使用openpyxl和docx包详解,图表入门 课后作业及答案
1、创建一个名为《课程》的excel文件,再分别创建《学生表》、《课程表》、《课时数》三个页签,设置《课程表》为当前页签,保存到C盘根目录。
import openpyxl
wb = openpyxl.Workbook()
wb.create_sheet(title="学生表",index=0)
wb.create_sheet(title="课程表",index=1)
wb.create_sheet(title="课时数",index=2)
wb._active_sheet_index = 1
wb.save("C://课程.xlsx")
2、打开《课程表》,删除默认《Sheet》页签, 修改《课时数》页签名称为《课时统计》,打开《课程表》页签,设置A1的内容为"我的课程表",要求黑体、20号字、加粗,设置A1行高为30,固定(冻结)第一行,操作完后保存。
import openpyxl
from openpyxl.styles import Font
wb = openpyxl.load_workbook("C://课程.xlsx")
del wb["Sheet"]
wb["课时数"].title = "课时统计"
sheet = wb.active
sheet["A1"] = "我的课程表"
htFont = Font(name="黑体",size=20,bold=True)
sheet["A1"].font = htFont
sheet.row_dimensions[1].height = 30
sheet.freeze_panes = "A2"# 冻结第一行,所以坐标选A2即可
wb.save("C://课程.xlsx")
3、打开《课程表》,打开《课程表》页签,将[A1:E1]合并,水平居中垂直居中对齐;在第二行循环插入[“星期1”,“星期2”,“星期3”,“星期4”,“星期5”],并设定每一列宽度为15,加粗并水平居中,操作完后保存。
提示:
- 居中设置需要引入包from openpyxl.styles import Alignment。
- 对单元格A1设置水平及垂直居中的方法:sheet[“A1”].alignment = Alignment(horizontal=“center”, vertical=“center”)。
- horizontal="center"水平居中,vertical="center"垂直居中。
import openpyxl
from openpyxl.styles import Alignment,Font
from openpyxl.utils import get_column_letter
wb = openpyxl.load_workbook("C://课程.xlsx")
sheet = wb["课程表"]
sheet.merge_cells("A1:E1")
sheet["A1"].alignment = Alignment(horizontal="center", vertical="center")
for i in range(1,6):
sheet.cell(row=2,column=i,value="星期{}".format(i)) # 填充数据
sheet.column_dimensions[get_column_letter(i)].width = 15 # 每一列设置宽度
boldFont = Font(bold=True)
sheet.cell(row=2,column=i).font, sheet.cell(row=2,column=i).alignment = boldFont, Alignment(horizontal="center")
wb.save("C://课程.xlsx")
4、打开《课程表》,打开《课程表》页签,使用append方式逐行填充下方课表内容,内容水平居中,输出最大行数和最大列数,操作完后保存。
import openpyxl
from openpyxl.styles import Alignment
wb = openpyxl.load_workbook("C://课程.xlsx")
sheet = wb.active
for note in ["语文","数学","英语","物理","历史","生物"]:
sheet.append([note] * 5)
sheet.append(["化学","地理","政治","美术","音乐"])
for rowObject in sheet["A3":"E9"]:
for cellObject in rowObject:
cellObject.alignment = Alignment(horizontal="center")
print("maxRow={},maxColumn={}".format(sheet.max_row,sheet.max_column))
wb.save("C://课程.xlsx")
maxRow=9,maxColumn=5
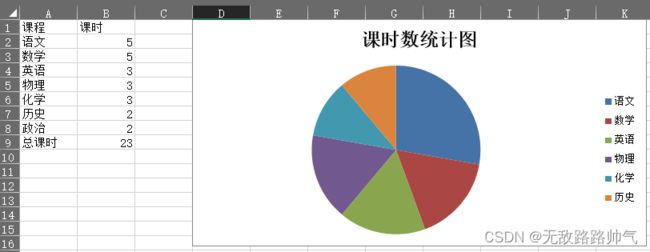
*(挑战)5、打开《课时统计》页签,填充以下数据,最后一行为总课时数,将每种课时绘制成饼图在单元格D1输出,操作完后保存。
提示:
- 引入饼状图相关包 from openpyxl.chart import Reference,PieChart 。
- pie = PieChart()生成饼状图对象。
- labels = Reference() 设置标签。
- datas = Reference() 设置数据。
- pie.add_data(datas,titles_from_data=True) 填充数据。
- pie.set_categories(labels) 填充标签。
- pie.title=" " 设置饼图标题。
- sheet.add_chart(pie,“D1”) 饼图添加进表格
| 课程 | 课时 |
| 语文 | 5 |
| 数学 | 5 |
| 英语 | 3 |
| 物理 | 3 |
| 化学 | 3 |
| 历史 | 2 |
| 政治 | 2 |
| 总课时 | SUM(B2:B9) |
import openpyxl
from openpyxl.chart import Reference,PieChart
wb = openpyxl.load_workbook("C://课程.xlsx")
sheet = wb["课时统计"]
data=[
["课程","课时"],
["语文",5],
["数学",5],
["英语",3],
["物理",3],
["化学",3],
["历史",2],
["政治",2],
["总课时",""]
]
for row in data:# 填充表格
sheet.append(row)
# 计算公式
sumcord = "=SUM(B2:%s)" % ("B"+str(sheet.max_row-1))
# 将计算结果填入
sheet.cell(row=sheet.max_row,column=sheet.max_column).value = sumcord
wb.save("C://课程.xlsx")
# 绘制饼状图
pie = PieChart()
labels = Reference(sheet,min_col=1,min_row=2,max_row=sheet.max_row-1,max_col=1)#课程标签
datas = Reference(sheet,min_col=2,min_row=2,max_row=sheet.max_row-1,max_col=2)#课时
pie.add_data(datas,titles_from_data=True)#饼图填充数据
pie.set_categories(labels)#设置标签
pie.title="课时数统计图"
# 将饼图填入表格
sheet.add_chart(pie,"D1")
wb.save("C://课程.xlsx")