【点云处理之论文狂读扩展版2】—— Transformer in Transformer
TnT:Transformer的改进版
- 摘要
- 1.引言
- 2.方法
-
- 2.1 Preliminaries
- 2.2Transformer in Transformer
- 2.3 Complexity Analysis
- 2.4 Network Architecture
- 3. 实验
- 生词
摘要
- 问题:图像有着很复杂且较多的细节,以patch为单位进行划分还远不能在不同的尺度和位置上发掘目标的特征
- 解决方法:局部patch中的attention对于构建高性能的视觉transformer也是很重要的,因此构建了一个新的架构 Transformer iN Transformer (TNT)
- 技术细节:
(1)将局部patch(16×16)看作为visual sentences,然后进一步将他们划分为更小的patch(4×4),称为visual words
(2)每个word的注意力将用给定的visual sentences中的其他wordd来计算,计算成本可以忽略不计
(3)words和sentences的特征会被聚合以提高表示能力 - 代码详见https://github.com/huawei-noah/CV-Backbones
1.引言
- Self-attention ——> Non-local networks
- 与NLP任务不同,在CV任务中输入图像和ground truth label之间还存在着semantic gap ——> ViT
- 首先将局部patch看作为visual sentences,然后进一步将他们划分为更小的patch,称为visual words
- 然后在网络中嵌入一个sub-transformer挖掘visual words的特征和细节
- 每个visual sentences中,visual words间的特征和attention都使用shared network共同和计算,复杂度和参数可忽略不计
- words的特征将会和对应的visual sentences进行聚合
- class token可继续用于下游任务
2.方法
2.1 Preliminaries
MSA (Multi-head Self-Attention)
在Self-attention模块中,输入 X ∈ R N × d X \in \mathbb{R}^{N \times d} X∈RN×d会被线性变换到三个部分,queries Q = X W Q ∈ R N × d k Q= XW_{Q} \in \mathbb{R}^{N \times d_k} Q=XWQ∈RN×dk, keys K = X W K ∈ R N × d k K=X W_{K} \in \mathbb{R}^{N \times d_k} K=XWK∈RN×dk, 和 values V = X W V ∈ R N × d v V=X W_{V} \in \mathbb{R}^{N \times d_v} V=XWV∈RN×dv,其中 N N N是序列长度, d , d k , d v d,d_k,d_v d,dk,dv分别是输入、queries (keys) 和 values的维度。 W Q ∈ R d × d k , W K ∈ R d × d k , W V ∈ R d × d v W_{Q}\in \mathbb{R}^{d \times d_{k}}, W_{K}\in \mathbb{R}^{d \times d_{k}}, W_{V} \in \mathbb{R}^{d \times d_{v}} WQ∈Rd×dk,WK∈Rd×dk,WV∈Rd×dv是要学习的参数。The scaled dot-product attention操作可以表示为:
Attention ( Q , K , V ) = Softmax ( Q K T d k ) V \operatorname{Attention}(Q, K, V)=\operatorname{Softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V Attention(Q,K,V)=Softmax(dkQKT)V
最后,线性层用于产生输出。Multi-head Self-Attention便是将queries, keys 和 values分成 h h h个部分,并行执行attention函数,然后将每个head的输出进行拼接,映射到最终的输出。
MLP (Multi-Layer Perceptron)
MLP被用在Self-attention层之间,用于特征变换和非线性激活:
M L P ( X ) = F C ( σ ( F C ( X ) ) ) , F C ( X ) = X W + b M L P(X)=F C(\sigma(F C(X))), \quad F C(X)=X W+b MLP(X)=FC(σ(FC(X))),FC(X)=XW+b
LN (Layer Normalization)
在transformer中,LN是稳定训练和快速收敛的关键,LN被用在每个样本 x ∈ R d x \in \mathbb{R}^{d} x∈Rd 上:
L N ( x ) = x − μ δ ∘ γ + β L N(x)=\frac{x-\mu}{\delta} \circ \gamma+\beta LN(x)=δx−μ∘γ+β
其中 μ ∈ R , δ ∈ R \mu \in \mathbb{R}, \delta \in \mathbb{R} μ∈R,δ∈R分别是特征的平均值和标准差, ∘ \circ ∘表示元素间的乘法, γ ∈ R d , β ∈ R d \gamma \in \mathbb{R}^{d}, \beta \in \mathbb{R}^{d} γ∈Rd,β∈Rd是应该学习的仿射变换参数。
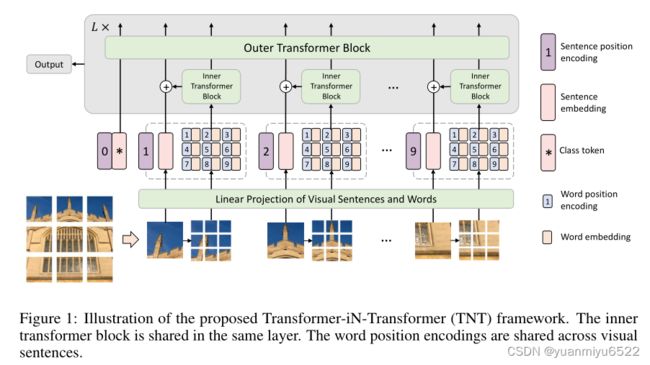
2.2Transformer in Transformer
给定一张2D图像,均匀将其分为 n n n个patch X = [ X 1 , X 2 , ⋯ , X n ] ∈ R n × p × p × 3 \mathcal{X}=\left[X^{1}, X^{2}, \cdots, X^{n}\right] \in \mathbb{R}^{n \times p \times p \times 3} X=[X1,X2,⋯,Xn]∈Rn×p×p×3,其中 ( p , p ) (p, p) (p,p)是每个patch的像素。TnT将这些块看作是visual sentences,每个patch进一步被分为 m m m个visual words:
X i → [ x i , 1 , x i , 2 , ⋯ , x i , m ] , X^{i} \rightarrow\left[x^{i, 1}, x^{i, 2}, \cdots, x^{i, m}\right], Xi→[xi,1,xi,2,⋯,xi,m],
其中 x i , j ∈ R s × s × 3 x^{i, j} \in \mathbb{R}^{s \times s \times 3} xi,j∈Rs×s×3表示第 i i i个visual sentence的第 j j j个visual word, ( s , s ) (s, s) (s,s) 是sub-patches的大小, j = 1 , 2 , ⋯ , m j=1,2, \cdots, m j=1,2,⋯,m。将visual words映射到word embedding:
Y i = [ y i , 1 , y i , 2 , ⋯ , y i , m ] , y i , j = F C ( Vec ( x i , j ) ) , Y^{i}=\left[y^{i, 1}, y^{i, 2}, \cdots, y^{i, m}\right], \quad y^{i, j}=F C\left(\operatorname{Vec}\left(x^{i, j}\right)\right), Yi=[yi,1,yi,2,⋯,yi,m],yi,j=FC(Vec(xi,j)),
其中 y i , j ∈ R c y^{i, j} \in \mathbb{R}^{c} yi,j∈Rc是第 j j j个word embedding, c c c 是word embedding的维度, Vec ( ⋅ ) \operatorname{Vec}(\cdot) Vec(⋅)是vectorization操作。
TnT中,有两个分支,一个处理visual sentence,另外一个处理visual sentence里的visual words。
-
对于word embedding,利用inner transformer block T in T_{\text {in}} Tin来找到visual words之间的关系:
Y l ′ i = Y l − 1 i + MSA ( LN ( Y l − 1 i ) ) Y l i = Y l ′ i + MLP ( LN ( Y l ′ i ) ) . \begin{aligned} Y_{l}^{\prime i} &=Y_{l-1}^{i}+\operatorname{MSA}\left(\operatorname{LN}\left(Y_{l-1}^{i}\right)\right) \\ Y_{l}^{i} &=Y_{l}^{\prime i}+\operatorname{MLP}\left(\operatorname{LN}\left(Y_{l}^{\prime i}\right)\right) . \end{aligned} Yl′iYli=Yl−1i+MSA(LN(Yl−1i))=Yl′i+MLP(LN(Yl′i)).
其中 l = 1 , 2 , ⋯ , L l=1,2, \cdots, L l=1,2,⋯,L表示第 l l l个block, L L L是blocks的总数。输出结果表示为 Y l = [ Y l 1 , Y l 2 , ⋯ , Y l n ] \mathcal{Y}_{l}=\left[Y_{l}^{1}, Y_{l}^{2}, \cdots, Y_{l}^{n}\right] Yl=[Yl1,Yl2,⋯,Yln]。 -
在处理sentence时,先将sentence转换为 sentence embedding Z 0 = [ Z class , Z 0 1 , Z 0 2 , ⋯ , Z 0 n ] ∈ R ( n + 1 ) × d \mathcal{Z}_{0}=\left[Z_{\text {class }}, Z_{0}^{1}, Z_{0}^{2}, \cdots, Z_{0}^{n}\right] \in \mathbb{R}^{(n+1) \times d} Z0=[Zclass ,Z01,Z02,⋯,Z0n]∈R(n+1)×d, 其中 Z class Z_{\text {class }} Zclass 是class token,初始值设置为0。 在每一层中,word embeddings的序列会通过线性映射的方式转换到sentence embedding的空间域,并与sentence embedding进行相加:
Z l − 1 i = Z l − 1 i + F C ( Vec ( Y l i ) ) , Z_{l-1}^{i}=Z_{l-1}^{i}+F C\left(\operatorname{Vec}\left(Y_{l}^{i}\right)\right), Zl−1i=Zl−1i+FC(Vec(Yli)),
通过上式相加的操作后sentence embedding的表示通过word-level features进行了增强,然后使用标准的outer transformer block处理上述的sentence embedding:
Z ′ l = Z l − 1 + MSA ( LN ( Z l − 1 ) ) , Z l = Z l ′ + MLP ( LN ( Z ′ l ) ) \begin{aligned} \mathcal{Z}^{\prime}{ }_{l} &=\mathcal{Z}_{l-1}+\operatorname{MSA}\left(\operatorname{LN}\left(\mathcal{Z}_{l-1}\right)\right), \\ \mathcal{Z}_{l} &=\mathcal{Z}_{l}^{\prime}+\operatorname{MLP}\left(\operatorname{LN}\left(\mathcal{Z}^{\prime}{ }_{l}\right)\right) \end{aligned} Z′lZl=Zl−1+MSA(LN(Zl−1)),=Zl′+MLP(LN(Z′l))
该outer transformer block T out T_{\text {out }} Tout 被用于建立sentence embeddings之间的关系。
总之,TNT block的输入和输出同时包含了word embeddings 和 sentence embeddings:
Y l , Z l = T N T ( Y l − 1 , Z l − 1 ) . \mathcal{Y}_{l}, \mathcal{Z}_{l}=T N T\left(\mathcal{Y}_{l-1}, \mathcal{Z}_{l-1}\right) . Yl,Zl=TNT(Yl−1,Zl−1).
在TNT block中,inner transformer block被用于构建visual words之间的关系,提取局部特征。outer transformer block捕获sentences序列之间的固有信息。通过将TNT block堆叠 L L L 次,我们构建了transformerin-transformer网络。
Position encoding
空间信息很重要,在sentence embeddings and word embeddings中都加了对应的position encodings,在本文中使用了标准的1D position encodings。
- 对于sentence:
Z 0 ← Z 0 + E sentence \mathcal{Z}_{0} \leftarrow \mathcal{Z}_{0}+E_{\text {sentence }} Z0←Z0+Esentence ,
其中 E sentence ∈ R ( n + 1 ) × d E_{\text {sentence }} \in \mathbb{R}^{(n+1) \times d} Esentence ∈R(n+1)×d是 sentence 的position encodings。 - 对于sentence中的word,便是将word position encoding与word position encoding相加:
Y 0 i ← Y 0 i + E word , i = 1 , 2 , ⋯ , n Y_{0}^{i} \leftarrow Y_{0}^{i}+E_{\text {word }}, i=1,2, \cdots, n Y0i←Y0i+Eword ,i=1,2,⋯,n
其中 E word ∈ R m × c E_{\text {word }} \in \mathbb{R}^{m \times c} Eword ∈Rm×c是word的position encodings,该position encodings在sentence中是共享权值的。
这样,sentence position encoding可以保留全局空间信息,word position encoding能够用于保留局部相对信息。
2.3 Complexity Analysis
标准的transformer block包含了两个部分, the multi-head self-attention 和 multi-layer perceptron。multi-head self-attention的FLOPs 是 2 n d ( d k + d v ) + n 2 ( d k + d v ) 2 n d\left(d_{k}+d_{v}\right)+n^{2}\left(d_{k}+d_{v}\right) 2nd(dk+dv)+n2(dk+dv),multi-layer perceptron的复杂度是 2 n d v r d v 2 n d_{v} r d_{v} 2ndvrdv ,其中 r r r是MLP中隐藏层中的dimension expansion ratio。总之,标准transformer block的FLOPs为:
FLOPs T = 2 n d ( d k + d v ) + n 2 ( d k + d v ) + 2 n d d r . \text { FLOPs}_{T}=2 n d\left(d_{k}+d_{v}\right)+n^{2}\left(d_{k}+d_{v}\right)+2 n d d r . FLOPsT=2nd(dk+dv)+n2(dk+dv)+2nddr.
由于 r r r通常设置为4,input, key (query)和 value 的维度通常设置的是一样的,FLOPs可以简化为:
F L O P s T = 2 n d ( 6 d + n ) . \mathrm{FLOPs}_{T}=2 n d(6 d+n) . FLOPsT=2nd(6d+n).
参数的数量为:
Params T = 12 d d . \text { Params }_{T}=12 d d . Params T=12dd.
本文提出的transformer block包含了3个部分,an inner transformer block T i n T_{i n} Tin,an outer transformer block T out T_{\text {out }} Tout and a linear layer。 T in T_{\text {in }} Tin 和 T out T_{\text {out }} Tout 的FLOPs分别是 2 n m c ( 6 c + m ) 2 n m c(6 c+m) 2nmc(6c+m) 和 2 n d ( 6 d + n ) 2 n d(6 d+n) 2nd(6d+n),linear layer的FLOPs是 n m c d n m c d nmcd。总之TnT block的FLOPs为:
F L O P s T N T = 2 n m c ( 6 c + m ) + n m c d + 2 n d ( 6 d + n ) . \mathrm{FLOPs}_{T N T}=2 n m c(6 c+m)+n m c d+2 n d(6 d+n) . FLOPsTNT=2nmc(6c+m)+nmcd+2nd(6d+n).
参数为:
P a r a m s T N T = 12 c c + m c d + 12 d d . \mathrm{Params}_{T N T}=12 c c+m c d+12 d d . ParamsTNT=12cc+mcd+12dd.
尽管在TnT中加了额外两项,但是FLOPs增加的数量很小,因为 c ≪ d c \ll d c≪d , O ( m ) ≈ O ( n ) \mathcal{O}(m) \approx \mathcal{O}(n) O(m)≈O(n) 。以较小的牺牲换取较高的性能,很nice。
2.4 Network Architecture
默认情况下,patch的大小为16×16,sub-patch的大小为 m = 4 ⋅ 4 = 16 m = 4 · 4 = 16 m=4⋅4=16
TnT有三种变体:
- TNT-Ti 6.1M
- TNT-S 23.8M
- TNT-B 65.6M
3. 实验
下次再写
生词
- granularity n.粒度
- excavate v. 挖掘