m基于kmeans和SVM的网络入侵数据分类算法matlab仿真

目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

---

1.算法描述

       首先计算整个数据集合的平均值点，作为第一个初始聚类中心C1；

       然后分别计算所有对象到C1的欧式距离d，并且计算每个对象在半径R的范围内包含的对象个数W。

       此时计算P=u*d+(1-u)*W，所得到的最大的P值所对应的的对象作为第二个初始聚类中心C2。

       同样的方法，分别计算所有对象到C2的欧式距离d，并且计算每个对象在半径R的范围内包含的对象个数W，所得到的最大的P值所对应的的对象作为第二个初始聚类中心C3。

       从这三个初始聚类中心开始聚类划分。对于一个待分类的对象，计算它到现有聚类中心的距离，若（这个距离）<（现有各个聚类中心距离的最小值），则将这个待分类对象分到与它相距最近的那一类；如果（这个距离）>（现有各个聚类中心距离的最小值），则这个待分类对象就自成一类，成为一个新的聚类中心，然后对所有对象重新归类。

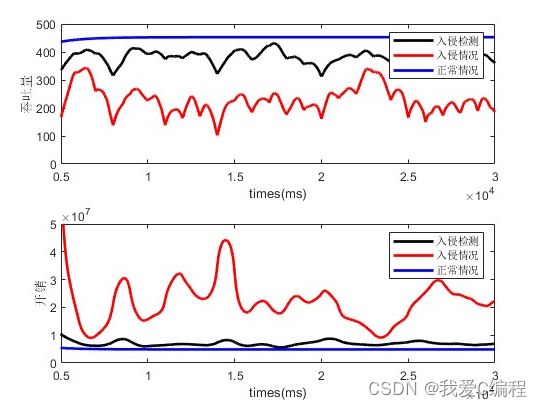
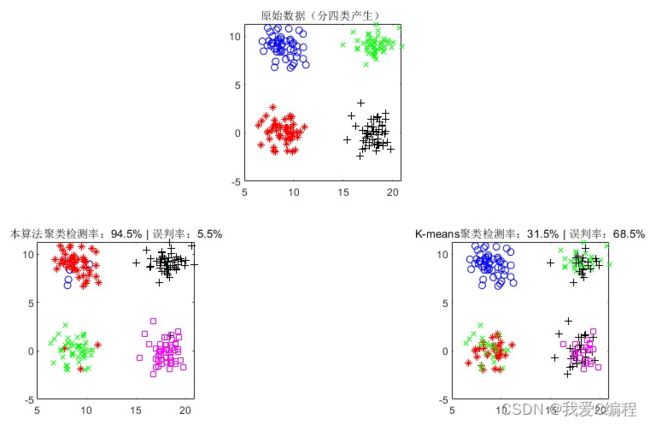
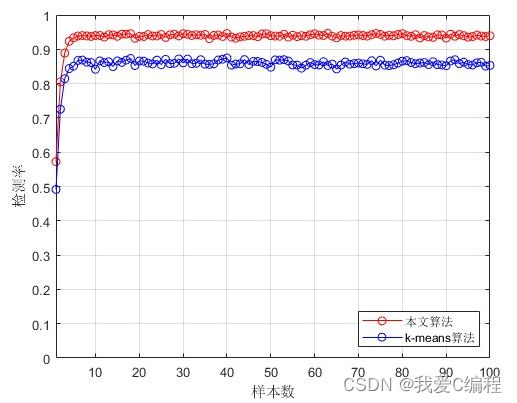
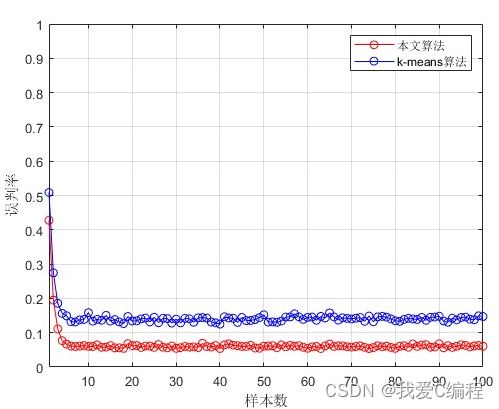
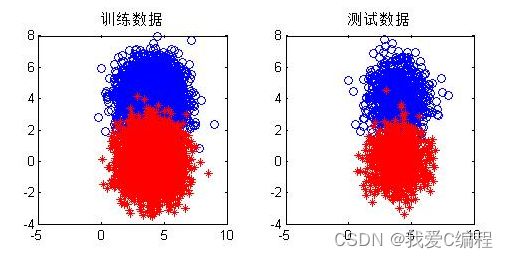
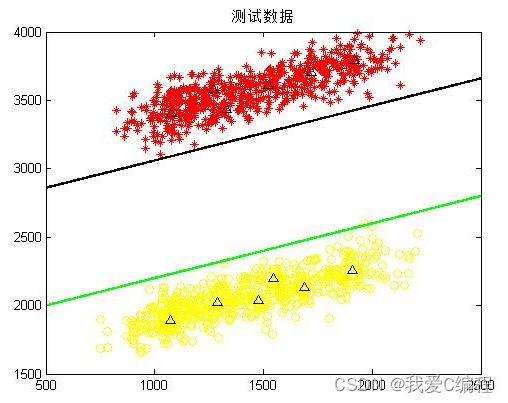
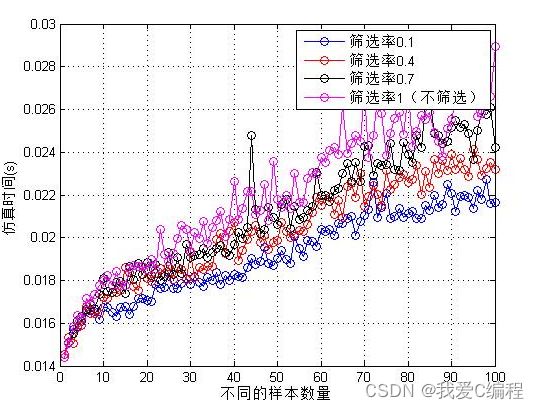
        如果找到新的聚类中心，在重新计算聚类的中心后。对目前形成的K+1 个聚类计算 DBInew 的值，和未重新分配对象到这 k+1 个类之前计算的 DBIold进行比较，如果 DBInew

聚类仿真图：

1.和K-means算法比较的检测率

2.和K-means算法比较的误判率

       特征提取：提取对检测最有用、最利于检测出攻击的那些参数。所用到的特征提取方案是利用“信息增益”，选出各特征参数中信息增益(Information Gain)最大的那些特征在检测时使用，这个做之前应该需要对数据先标准化和归一化一下。具体操作：

        究竟选多少个特征可以让检测的精度最高呢？我论文里是先将各个特征的信息增益从高到低排序，然后依次往下取K个，用K-means算法对节点进行分类达到检测的作用，计算当检测率最高的时候所对应 K值，即意为选多少个特征。

        经过特征提取后，之后所说的样本，他们的属性都只由特征提取后的那些特征来代表了。

        SVM训练样本筛选：假定有正常和攻击两类样本，将两类样本分别用K-means聚类，将这些聚类中心点作为新的样本点。然后在正常类中，计算每个新样本点在异常类中距离自己最近的M（假定M=3）个样本点，从而在异常类中假设找到P个样本点。异常类中的这P个样本点找到在正常类中距离自己最近的M个样本点，假定找到了Q个样本点。此时，这P+Q个样本点就是新选出的SVM训练样本。

2.仿真效果预览

matlab2013b仿真结果如下：

3.MATLAB核心程序

is_continue = 1;
C           = [C1;C2;C3];
R           = [R1;R2;R3];
Leg         = ones(length(Attack_Dat),1);
K           = 3;
CNT         = 0;
while(is_continue == 1)
    CNT = 0;
    for i = 1:length(Attack_Dat)
        for j = 1:size(C,1)
            d(i,j) = func_dis(Attack_Dat(i,:),C(j,:));
        end
        [VV,II] = min(d(i,:));
        if VV <= min(R)
            Leg(i) = II;
            CNT = CNT + 1;
        else
            K = K + 1;
            Leg(i) = K;
            C = [C;Attack_Dat(i,:)];
            R = [R;alpha*mean(func_dis(Attack_Dat,Attack_Dat(i,:)))];
        end
    end 
    
    if CNT == length(Attack_Dat)
       is_continue = 0;
    else
       is_continue = 1; 
    end
end

Tmps = unique(Leg);
if min(Tmps) > 1
   Leg = Leg - (min(Tmps)-1);
end
Leg = sort(Leg);
Leg = Leg-1;
%检测率
Right1 = 100*(length(find(Leg == T))/length(Attack_Dat))
%误判率
Error1 = 100*(1-length(find(Leg == T))/length(Attack_Dat))

%对比算法K-means  
%对比算法K-means    
KK         = length(unique(Leg));
opts       = statset('Display','final');
X          = Attack_Dat;
[idx,ctrs] = kmeans(X,KK,'Distance','city','Replicates',10,'Options',opts);
idx        = sort(idx);
%检测率
Right2 = 100*(length(find(idx == T))/length(X))
%误判率
Error2 = 100*(1-length(find(idx == T))/length(X))


attack1 = [Attack_Dat(:,:),Leg];

%步骤3：SVM
%步骤3：SVM
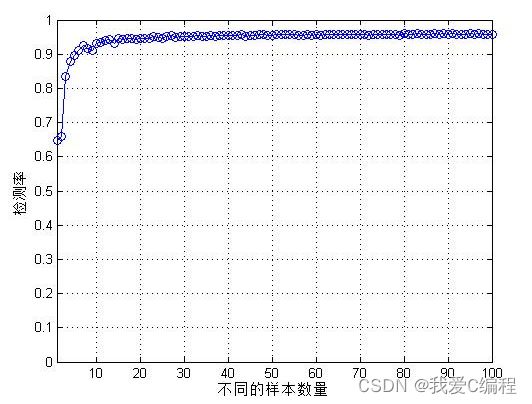
%特征选取时，选取的特征数量所对应的的检测率的仿真图
POS = attack1(1:length(Attack_Dat)/2,:);
NEG = attack1(length(Attack_Dat)/2+1:end,:);
%将数据随机产生训练集合和测试集合
INDD= (1:length(POS));


Attack_Dat_train = [POS(INDD(1:round(2/3*length(POS))),1:end-1);NEG(INDD(1:round(2/3*length(POS))),1:end-1)];
T_train          = [POS(INDD(1:round(2/3*length(POS))),end)    ;NEG(INDD(1:round(2/3*length(POS))),end)];

Attack_Dat_test = [POS(INDD(round(2/3*length(POS)))+1:end,1:end-1);NEG(INDD(round(2/3*length(POS)))+1:end,1:end-1)];
T_test          = [POS(INDD(round(2/3*length(POS)))+1:end,end)    ;NEG(INDD(round(2/3*length(POS)))+1:end,end)];


%训练集合
POS_train = Attack_Dat_train(find(T_train==1),:);
NEG_train = Attack_Dat_train(find(T_train==2),:);
%测试集合
POS_test = Attack_Dat_test(find(T_test==1),:);
NEG_test = Attack_Dat_test(find(T_test==2),:);


%随机选择K个样本进行分类，并计算对应的检测率
K     = 60;
KK    = 2;
Alpha = 0.7;
Indes = 0;

Index = 0;
Indes = Indes + 1;

tic
Index = Index + 1;

IND        = randperm(length(POS_train));
POS_train2 = POS_train(IND(1:K),:);
NEG_train2 = NEG_train(IND(1:K),:);
%Kmeans
opts       = statset('Display','final');
X          = [POS_train2;NEG_train2];
[idx,ctrs] = kmeans(X,KK,'Distance','city','Replicates',10,'Options',opts);
%准备SVM训练分类——SVM训练样本的选择
Q          = round(Alpha*size(POS_train2,1));
if Q == 0
   Q = 1;
end
P          = round(Alpha*size(NEG_train2,1));
if P == 0
   P = 1;
end    

%正样本
d_pos      = func_dis2(POS_train2,ctrs(1,:));
%选择距离最近的M个
[Vpos,Ipos]= sort(d_pos);
POS_train_final = POS_train2(Ipos(1:Q),:);
%负样本
d_neg      = func_dis2(NEG_train2,ctrs(2,:));
%选择距离最近的N个
[Vneg,Ineg]= sort(d_neg);
NEG_train_final = NEG_train2(Ipos(1:P),:);

%SVM训练
options = optimset('maxiter',10000);
Ps      = [POS_train_final;NEG_train_final];
Ts      = [ones(length(POS_train_final),1);2*ones(length(NEG_train_final),1)];
SvmNet  = svmtrain(Ps,(Ts),'Kernel_Function','linear','Polyorder',2,'quadprog_opts',options);  

%SVM测试
Test_Dat = [POS_test;NEG_test];
Classify = svmclassify(SvmNet,Test_Dat);

%计算检测率
times(Index) = toc;
Right(Index) = length(find((Classify)==T_test))/length(T_test);
clc;
05_016_m

4.完整MATLAB

V