联邦学习-论文阅读-AAAI-Game of Gradients: Mitigating Irrelevant Clients in Federated Learning
1、Game of Gradients: Mitigating Irrelevant Clients in Federated Learning(选择客户端,主要为把不相关的客户端剔除出去)
1、概要
中心服务器无法知道每个客户端所拥有的数据的品质如何,因此在FL设置写如果选择相关客户端的问题十分复杂。将FL建模为一个合作博弈,将从作为客户端接收到的更新以及模型在服务器验证数据集上的性能作为特征函数。并计算每个客户机的Shapley值,并使用它来评估其与服务器的学习目标的相关性。提出了一种基于Shapley值的联合平均算法(S-FedAvg),该算法使服务器能够以高概率选择相关的客户端。
2、动机
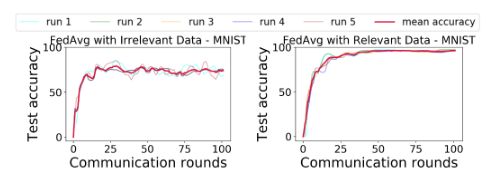
例如任务发布方只要求对{0,2,4,6,8}进行分类,故客户端所拥有的{1,3,5,7,9}即为无关数据,故其上传的梯度会对全局模型产生及其负面的影响。(MNIST数据集)
左边设置:6个本地客户端的数据为{0,2,4,6,8},4个客户端的数据为{1,3,5,7,9}
右边设置:整个数据集平均分给10个客户端
3、联邦学习范式
联邦学习框架由一组 S = 1 , 2 , . . . , K S={1,2,...,K} S=1,2,...,K客户端/节点组成,其中每个客户端拥有其私有数据 ∣ D k ∣ \begin{vmatrix}\mathbb{D}_k\end{vmatrix} ∣∣Dk∣∣, ∣ D k ∣ = n k \begin{vmatrix}\mathbb{D}_k\end{vmatrix}=n_k ∣∣Dk∣∣=nk, n k n_k nk为第 k k k个客户端拥有的训练样本数,则 n = ∑ k ∈ K n k n=\sum_{k{\in}K}{n_k} n=∑k∈Knk为所有客户端拥有的总样本数,中心服务器为 C C C。目标为训练一个分类器 f ( θ ) f(\theta) f(θ),其中 θ \theta θ为通过聚合得到的全局模型(一个参数向量),并且期望这个模型能够在测试集上由良好的结果 D t e s t D_{test} Dtest。在联邦学习中,中心服务器的目标为:
m i n θ l ( θ ) = ∑ k = 1 K n k n l k ( θ ) min_{\theta}l(\theta)=\sum_{k=1}^{K}\frac{n_k}{n}l_k(\theta) minθl(θ)=k=1∑Knnklk(θ)
其中 l k ( θ ) = 1 n k ∑ i ∈ D k l i ( θ ) l_k(\theta)=\frac{1}{n_k}\sum_{i{\in}\mathbb{D}_k}{l_i(\theta)} lk(θ)=nk1∑i∈Dkli(θ)。
机器学习中 l i ( θ ) = l ( y i , f θ ( x i ) ) {l_i(\theta)}={l(y_i,f_{\theta}(x_i))} li(θ)=l(yi,fθ(xi))为对数据 ( x i , y i ) {(x_i,y_i)} (xi,yi)用模型参数 θ \theta θ预测的损失。
在联邦学习的第 t t t轮,中心服务器随机的选取部分客户端 S t S^t St,被选取的客户端从中心服务器下载全局模型 θ t {\theta}^t θt并用其初始化自己的本地模型,然后使用自己的本地数据进行训练。最后每个被选取的客户端 k k k会将其训练得到的本地模型 δ k t + 1 {\delta}_k^{t+1} δkt+1发送给中心服务器,然后得到新的全局模型状态 θ t + 1 {\theta}^{t+1} θt+1。知道全局模型收敛。
4、提出方法
1)整体概述
提出的算法将客户端视为合作博弈中的玩家,并从中得到更新;然后推导出客户端的shapley值,并使用其来计算客户端的相关性。
2)合作博弈(Cooperative Games)
对于一个联盟博弈中(a coalitional game),定义 N = 1 , 2 , . . . , n N={1,2,...,n} N=1,2,...,n为其参与者集, C C C为 N N N的任意子集,代表每个联盟,特征函数 v : w B → R v:w^B\rightarrow\mathbb{R} v:wB→R代表该联盟可以获得的回报,其中 v ( ϕ ) = 0 v(\phi)=0 v(ϕ)=0;认为一个联盟博弈即为一个元组 ( N , v ) (N,v) (N,v)。
()
3)Shapley值
(合作博弈论中,Shapley value被用来公平地分配信用或贡献给每个玩家(参与者,每次一个参与者加入整个合作游戏中时,整体会有一个收益,每个参与者会有一个边际收益,Shapley value即为该参与者的所有边际值的平均)。
Shapley建议通过考虑每个玩家可能属于的所有联盟的边际贡献来评估每个玩家在游戏中的角色。这种边际贡献的某个加权和构成了玩家从联盟博弈中获得的收益,称为Shapley值。故可以将每个参与者 i i i应该分配的收益定义为:
S V i ( v ) = ∑ C ⊆ A \ { i } ∣ C ∣ ! ( ∣ N ∣ − ∣ C ∣ − 1 ) ! ∣ N ∣ ! [ v ( C ∪ i ) − v ( C ) ] SV_i(v)=\sum_{C{\subseteq}A\backslash\{i\}}{\frac{\begin{vmatrix}C\end{vmatrix}!(\begin{vmatrix}N\end{vmatrix}-\begin{vmatrix}C\end{vmatrix}-1)!}{\begin{vmatrix}N\end{vmatrix}!}}[v(C\cup{i})-v(C)] SVi(v)=C⊆A\{i}∑∣∣N∣∣!∣∣C∣∣!(∣∣N∣∣−∣∣C∣∣−1)![v(C∪i)−v(C)]
4)计算客户端的相关性( φ \varphi φ)
联邦学习中,一共有 S t S^t St个客户端,在 t t t轮,全局模型为 θ t {\theta}^t θt,第 k k k个客户端用其训练出来的模型 θ k t + 1 {\theta}_k^{t+1} θkt+1,此时该客户端上传其模型差距至服务器即
δ k t + 1 = θ k t + 1 − θ t {\delta}_k^{t+1}={\theta}_k^{t+1}-{\theta}^t δkt+1=θkt+1−θt
此时中心服务器利用其验证集与合作博弈共同计算客户端的相关性。
可以将上述定义为一个合作博弈:
( δ t + 1 , v ) ({\delta}^{t+1},v) (δt+1,v)
其中 δ t + 1 = { δ s t + 1 } s ∈ S t {\delta}^{t+1}=\{{\delta}_s^{t+1}\}_{s{\in}S^t} δt+1={δst+1}s∈St, v v v为特征函数用于计算联盟 X X X的贡献(一个值代表了这个联盟的模型在测试集 D V D_V DV上的性能), X X X为 S t S^t St的子集。
X X X联盟的模型以及特征函数分别为:(?)
θ X t + 1 = θ t + 1 ∣ X ∣ ∑ s ∈ X δ s t + 1 {\theta}_X^{t+1}={\theta}^{t}+\frac{1}{\begin{vmatrix}X\end{vmatrix}}\sum_{s{\in}X}{\delta}_s^{t+1} θXt+1=θt+∣∣X∣∣1s∈X∑δst+1
v ( X , D V ) = P ( f θ X t + 1 , D V ) v(X,D_V)=\mathcal{P}(f_{\theta_X^{t+1}},D_V) v(X,DV)=P(fθXt+1,DV)
也就是说特征函数 v v v为 X X X联盟的模型 θ X t + 1 {\theta}_X^{t+1} θXt+1在验证集 D V D_V DV上的准确率。
基于上述的定义的合作博弈以及Shapley值计算方法可以计算出每个客户端的Shapley值 s v ( s ) sv(s) sv(s)其中 s ∈ S t s\in S^t s∈St
定义客户端的相关性:定义一个相关向量 φ = ( φ 1 , φ 2 , . . . , φ K ) \varphi=(\varphi_1,\varphi_2,...,\varphi_K) φ=(φ1,φ2,...,φK),其中 φ k \varphi_k φk代表第 k k k客户端的相关性,第 t = 0 t=0 t=0轮所有的初始 值都定义为 1 K \frac{1}{K} K1,对于每轮的相关性更新规则如下:
φ s = α ∗ φ s + β ∗ s v ( s ) ; ∀ s ∈ S t ( ? ) \varphi_s=\alpha*\varphi_s+\beta*sv(s);\forall s\in S_t(?) φs=α∗φs+β∗sv(s);∀s∈St(?)
φ s t + 1 = α ∗ φ s t + β ∗ s v ( s ) ; ∀ s ∈ S t \varphi_s^{t+1}=\alpha*\varphi_s^{t}+\beta*sv(s);\forall s\in S_t φst+1=α∗φst+β∗sv(s);∀s∈St
可以用 s o f t m a x ( ⋅ ) softmax(\cdot) softmax(⋅)估计每个每个客户端的相对相关性,即 P φ = s o f t m a x ( φ ) P_\varphi=softmax(\varphi) Pφ=softmax(φ)。
(合作博弈为研究玩家达成合作是如何分配合作时的收益,即收益分配问题;本文中,客户端不断加入训练过程获得一个模型,其特征函数为整体模型的准确率,可以理解为收益,准确率越大即收益越高,则Shapley值越大,故可以说明该成员的相关度越高(因为其参与的模型的准确度越高))
5、联邦学习流程(S-FedAvg)
(与普通的FedAvg没太大区别)
由于Shapely值计算涉及到 ∣ N ∣ ! \left| N \right|! ∣N∣!计算,计算量过大,故采取蒙特卡罗估计方法近似计算
观点阐述:
- 选择相关客户的问题还没有得到充分的探讨,这类问题称为Federated Relevant Client Selection (FRCS)。
- 每一轮中,只有一小部分客户被选中,因为增加更多的客户将导致超过某一点的回报递减。
- 如果客户端所持有的数据及其共享的更新有助于提高中心模型的性能,则称其为相关。如果客户机共享的更新对中心模型有害,我们将其称为无关。
- 本文对合作博弈的定义中,当客户端共享的更新与其他客户端共享的更新联合使用时,会对中心模型的性能产生负面影响,客户端将收到一个负的Shapley值。