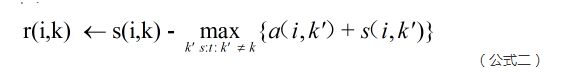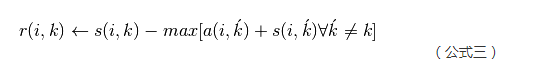数据挖掘——AP聚类算法学习
文章目录
-
- 一、算法简介
- 二、算法模型
-
-
- 1、相关概念
- 2、数学公式
-
- 三、算法流程_python代码
- 四、sklearn中AP算法使用
- 五、总结
- 参考资料:
一、算法简介
AP(Affinity Propagation)通常被翻译为近邻传播算法或者亲和力传播算法。是2007年的Science杂志上提出的一种新的聚类算法。AP算法的基本思想是将全部数据点都当作潜在的聚类中心(称为exemplar),然后数据点两两之间连线构成一个网络(相似度矩阵),再通过网络中各条边的消息(吸引度responsibility和归属度availability)传递计算出各样本的聚类中心。直到产生m个高质量的Exemplar(类似于质心),同时将其余的数据点分配到相应的聚类中。
二、算法模型
1、相关概念
-
Similarity (相似度): 点j作为点i的聚类中心的能力,记为S(i,j)。一般使用负的欧式距离,所以S(i,j)越大,表示两个点距离越近,相似度也就越高。使用负的欧式距离,相似度是对称的,如果采用其他算法,相似度可能就不是对称的。
-
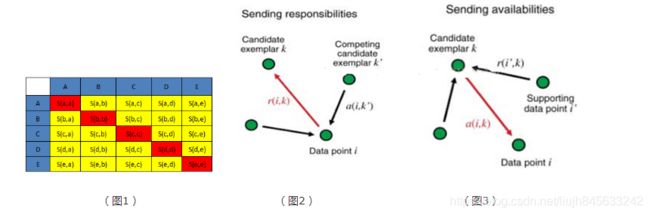
相似度矩阵:N个点之间两两计算相似度,这些相似度就组成了相似度矩阵。如图1所示的黄色区域,就是一个5*5的相似度矩阵(N=5)
-
preference(参考度):指点i作为聚类中心的参考度(不能为0),取值为S对角线的值(图1红色标注部分),此值越大,为聚类中心的可能性就越大。但是对角线的值为0,所以需要重新设置对角线的值,既可以根据实际情况设置不同的值,也可以设置成同一值。一般设置为S相似度值的中值。(有的说设置成S的最小值产生的聚类最少,但是在下面的算法中设置成中值产生的聚类是最少的)
-
Responsibility(吸引度):指点k适合作为数据点i的聚类中心的程度,记为r(i,k)。如图2红色箭头所示,表示点i给点k发送信息,是一个点i选点k的过程。
-
Availability(归属度):指点i选择点k作为其聚类中心的适合程度,记为a(i,k)。如图3红色箭头所示,表示点k给点i发送信息,是一个点k选点i的过程。
-
exemplar:指的是聚类中心。
-
Damping factor(阻尼系数):主要是起收敛作用的
-
r (i, k)加a (i, k)越大,则k点作为聚类中心的可能性就越大,并且i点隶属于以k点为聚类中心的聚类的可能性也越大
在实际计算应用中,最重要的两个参数(也是需要手动指定)是Preference和Damping factor。前者定了聚类数量的多少,值越大聚类数量越多;后者控制算法收敛效果。
2、数学公式
(1)吸引度迭代公式:
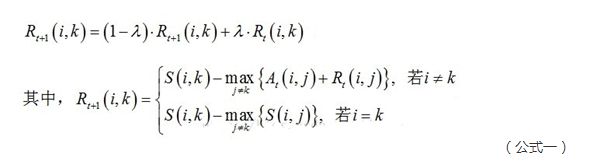
说明1:Rt+1(i,k)表示新的R(i,k),Rt(i,k)表示旧的R(i,k),也许这样说更容易理解。其中λ是阻尼系数,取值[0.5,1),用于算法的收敛。
说明2:网上还有另外一种数学公式:
说明:At+1(i,k)表示新的A(i,k),At(i,k)表示旧的A(i,k)。其中λ是阻尼系数,取值[0.5,1),用于算法的收敛。
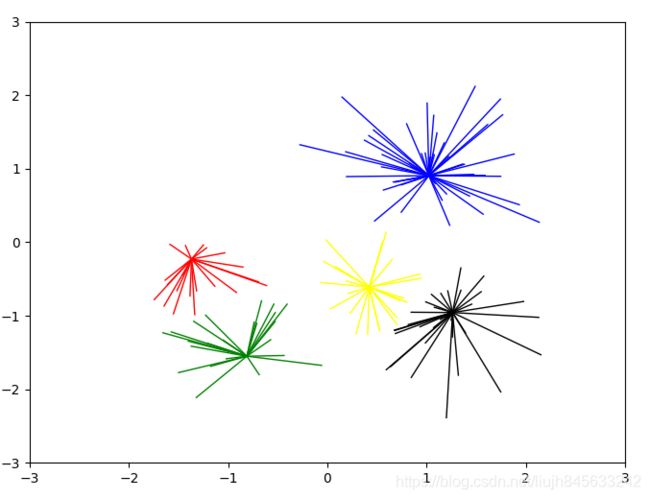
三、算法流程_python代码
from sklearn.datasets.samples_generator import make_blobs
import numpy as np
import matplotlib.pyplot as plt
'''
第一步:生成测试数据
1.生成实际中心为centers的测试样本300个,
2.Xn是包含150个(x,y)点的二维数组
3.labels_true为其对应的真是类别标签
'''
def init_sample():
## 生成的测试数据的中心点
centers = [[1, 1], [-1, -1], [1, -1]]
##生成数据
Xn, labels_true = make_blobs(n_samples=150, centers=centers, cluster_std=0.5,
random_state=0)
# 3数据的长度,即:数据点的个数
dataLen = len(Xn)
return Xn, dataLen
'''
第二步:计算相似度矩阵
'''
def cal_simi(Xn):
##这个数据集的相似度矩阵,最终是二维数组
simi = []
for m in Xn:
##每个数字与所有数字的相似度列表,即矩阵中的一行
temp = []
for n in Xn:
##采用负的欧式距离计算相似度
s = -np.sqrt((m[0] - n[0]) ** 2 + (m[1] - n[1]) ** 2)
temp.append(s)
simi.append(temp)
##设置参考度,即对角线的值,一般为最小值或者中值
# p = np.min(simi) ##11个中心
# p = np.max(simi) ##14个中心
p = np.median(simi) ##5个中心
for i in range(dataLen):
simi[i][i] = p
return simi
'''
第三步:计算吸引度矩阵,即R
公式1:r(n+1) =s(n)-(s(n)+a(n))-->简化写法,具体参见上图公式
公式2:r(n+1)=(1-λ)*r(n+1)+λ*r(n)
'''
##初始化R矩阵、A矩阵
def init_R(dataLen):
R = [[0] * dataLen for j in range(dataLen)]
return R
def init_A(dataLen):
A = [[0] * dataLen for j in range(dataLen)]
return A
##迭代更新R矩阵
def iter_update_R(dataLen, R, A, simi):
old_r = 0 ##更新前的某个r值
lam = 0.5 ##阻尼系数,用于算法收敛
##此循环更新R矩阵
for i in range(dataLen):
for k in range(dataLen):
old_r = R[i][k]
if i != k:
max1 = A[i][0] + R[i][0] ##注意初始值的设置
for j in range(dataLen):
if j != k:
if A[i][j] + R[i][j] > max1:
max1 = A[i][j] + R[i][j]
##更新后的R[i][k]值
R[i][k] = simi[i][k] - max1
##带入阻尼系数重新更新
R[i][k] = (1 - lam) * R[i][k] + lam * old_r
else:
max2 = simi[i][0] ##注意初始值的设置
for j in range(dataLen):
if j != k:
if simi[i][j] > max2:
max2 = simi[i][j]
##更新后的R[i][k]值
R[i][k] = simi[i][k] - max2
##带入阻尼系数重新更新
R[i][k] = (1 - lam) * R[i][k] + lam * old_r
print("max_r:" + str(np.max(R)))
# print(np.min(R))
return R
'''
第四步:计算归属度矩阵,即A
'''
##迭代更新A矩阵
def iter_update_A(dataLen, R, A):
old_a = 0 ##更新前的某个a值
lam = 0.5 ##阻尼系数,用于算法收敛
##此循环更新A矩阵
for i in range(dataLen):
for k in range(dataLen):
old_a = A[i][k]
if i == k:
max3 = R[0][k] ##注意初始值的设置
for j in range(dataLen):
if j != k:
if R[j][k] > 0:
max3 += R[j][k]
else:
max3 += 0
A[i][k] = max3
##带入阻尼系数更新A值
A[i][k] = (1 - lam) * A[i][k] + lam * old_a
else:
max4 = R[0][k] ##注意初始值的设置
for j in range(dataLen):
##上图公式中的i!=k 的求和部分
if j != k and j != i:
if R[j][k] > 0:
max4 += R[j][k]
else:
max4 += 0
##上图公式中的min部分
if R[k][k] + max4 > 0:
A[i][k] = 0
else:
A[i][k] = R[k][k] + max4
##带入阻尼系数更新A值
A[i][k] = (1 - lam) * A[i][k] + lam * old_a
print("max_a:" + str(np.max(A)))
# print(np.min(A))
return A
'''
第5步:计算聚类中心
'''
##计算聚类中心
def cal_cls_center(dataLen, simi, R, A):
##进行聚类,不断迭代直到预设的迭代次数或者判断comp_cnt次后聚类中心不再变化
max_iter = 100 ##最大迭代次数
curr_iter = 0 ##当前迭代次数
max_comp = 30 ##最大比较次数
curr_comp = 0 ##当前比较次数
class_cen = [] ##聚类中心列表,存储的是数据点在Xn中的索引
while True:
##计算R矩阵
R = iter_update_R(dataLen, R, A, simi)
##计算A矩阵
A = iter_update_A(dataLen, R, A)
##开始计算聚类中心
for k in range(dataLen):
if R[k][k] + A[k][k] > 0:
if k not in class_cen:
class_cen.append(k)
else:
curr_comp += 1
curr_iter += 1
print(curr_iter)
if curr_iter >= max_iter or curr_comp > max_comp:
break
return class_cen
if __name__ == '__main__':
##初始化数据
Xn, dataLen = init_sample()
##初始化R、A矩阵
R = init_R(dataLen)
A = init_A(dataLen)
##计算相似度
simi = cal_simi(Xn)
##输出聚类中心
class_cen = cal_cls_center(dataLen, simi, R, A)
# for i in class_cen:
# print(str(i)+":"+str(Xn[i]))
# print(class_cen)
##根据聚类中心划分数据
c_list = []
for m in Xn:
temp = []
for j in class_cen:
n = Xn[j]
d = -np.sqrt((m[0] - n[0]) ** 2 + (m[1] - n[1]) ** 2)
temp.append(d)
##按照是第几个数字作为聚类中心进行分类标识
c = class_cen[temp.index(np.max(temp))]
c_list.append(c)
##画图
colors = ['red', 'blue', 'black', 'green', 'yellow']
plt.figure(figsize=(8, 6))
plt.xlim([-3, 3])
plt.ylim([-3, 3])
for i in range(dataLen):
d1 = Xn[i]
d2 = Xn[c_list[i]]
c = class_cen.index(c_list[i])
plt.plot([d2[0], d1[0]], [d2[1], d1[1]], color=colors[c], linewidth=1)
# if i == c_list[i] :
# plt.scatter(d1[0],d1[1],color=colors[c],linewidth=3)
# else :
# plt.scatter(d1[0],d1[1],color=colors[c],linewidth=1)
plt.show()
四、sklearn中AP算法使用
函数: sklearn.cluster.AffinityPropagation
2)主要参数:
- damping : 阻尼系数,取值[0.5,1)
- convergence_iter :比较多少次聚类中心不变之后停止迭代,默认15
- max_iter :最大迭代次数
- preference :参考度
3)主要属性
- cluster_centers_indices_ : 存放聚类中心的数组
- labels_ :存放每个点的分类的数组
- n_iter_ : 迭代次数
4)示例
preference(即p值)取不同值时的聚类中心的数目在代码中注明了。
import numpy as np
from sklearn.cluster import AffinityPropagation
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
## 生成测试数据
centers = [[1,1],[-1,-1],[1,-1]]
Xn, labels_true = make_blobs(n_samples=150, centers=centers,cluster_std=0.5,random_state=0)
p=-50
ap = AffinityPropagation(damping=0.5,max_iter=500, convergence_iter=30,preference=p).fit(Xn)
cluster_centers_indices = ap.cluster_centers_indices_
labels = ap.labels_
new_X = np.column_stack((Xn, labels))
n_clusters_ = len(cluster_centers_indices)
# for idx in cluster_centers_indices:
# print(Xn[idx])
# 图形展示
import matplotlib.pyplot as plt
from itertools import cycle
plt.close('all')
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
class_members = labels == k
cluster_center = Xn[cluster_centers_indices[k]]
plt.plot(Xn[class_members, 0], Xn[class_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
for x in Xn[class_members]:
plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
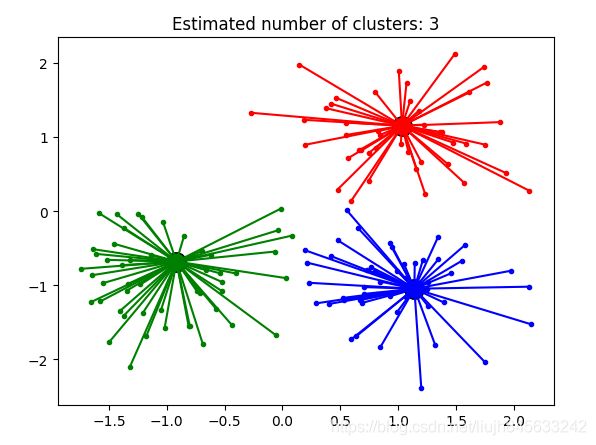
运行结果:
preference = -50 时
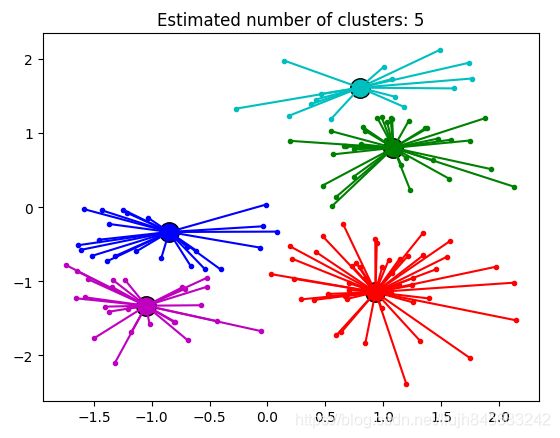
当 preference = -10 时,结果
五、总结
AP算法的优点:
1. 不需要制定最终聚类族的个数
2. 已有的数据点作为最终的聚类中心,而不是新生成一个族中心。
3. 模型对数据的初始值不敏感。
4. 对初始相似度矩阵数据的对称性没有要求。
5. 相比与k-centers聚类方法,其结果的平方差误差较小。
AP算法的不足:
1. AP算法需要事先计算每对数据对象之间的相似度,如果数据对象太多的话,内存放不下,若存在数据库,频繁访问数据库也需要时间。
2. AP算法的时间复杂度较高,一次迭代大概O(N3)
3. 聚类的好坏受到参考度和阻尼系数的影响。
综合来看,由于AP算法不适用均值做质心计算规则,因此对于离群点和异常值不敏感;同时其初始值不敏感的特性也能保持模型的较好鲁棒性。这两个突出特征使得它可以作为K-Means算法的一个有效补充,但在大数据量下的耗时过长,这导致它的适用范围只能是少量数据;虽然通过调整damping(收敛规则)可以在一定程度上提升运行速度(damping值调小),但由于算法本身的局限性决定了这也只是杯水车薪。
参考资料:
-
论文: https://www.psi.toronto.edu/affinitypropagation/FreyDueckScience07.pdf
-
聚类算法Affinity Propagation(AP)http://www.dataivy.cn/blog/%E8%81%9A%E7%B1%BB%E7%AE%97%E6%B3%95affinity-propagation_ap/
-
Affinity Propagation 聚类算法的通俗解释https://blog.csdn.net/notHeadache/article/details/89003044