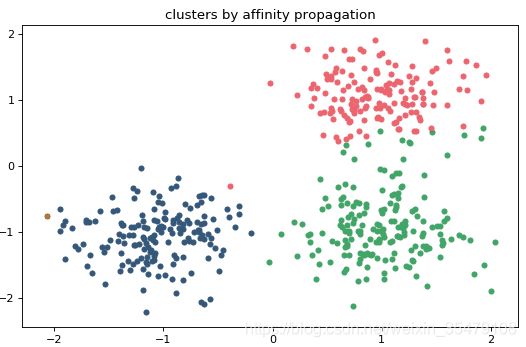
AP近邻传播算法理解
AP(Affinity propagation)基于近邻传播的半监督聚类算法。主要参考:AP总结
基本思想
- 通过信息传递机制 搜索 网络中 各个数据点的聚类中心,以及数据点与数据中心之间的隶属度关系
- 根据数据中心与顶点之间的隶属度关系来对待聚类数据集进行划分,形成若干个具有特定意义的子集。
优点
- 聚类过程中不需要明确确定与聚类个数相关的参数
- 聚类中心是待聚类数据的某个确切的数据点
- 算法的输入可以是对称或者非对称的相似性矩阵
- 多次执行AP算法得到的结果是一样的
缺点
- 算法的复杂度较高,为 O ( N ∗ N ∗ l o g N ) O(N*N*logN) O(N∗N∗logN),而K-Means只是 O ( N ∗ K ) O(N*K) O(N∗K)的复杂度。因此当N比较大时(N>3000),AP聚类算法往往需要算很久
名词解释及迭代理解
exemplar:指的是聚类中心。
similarity:数据点 i i i和点 j j j的相似度记为 S ( i , j ) S(i,j) S(i,j)。是指点 j j j作为点 i i i的聚类中心的相似度。
preference:数据点i的参考度称为 P ( i ) P(i) P(i)或 S ( i , i ) S(i,i) S(i,i)。是指点 i i i作为聚类中心的参考度。
Responsibility: r ( i , k ) r(i,k) r(i,k)用来描述点 k k k适合作为数据点 i i i的聚类中心的程度。
Availability: a ( i , k ) a(i,k) a(i,k)用来描述点 i i i选择点 k k k作为其聚类中心的适合程度。
Damping factor:阻尼系数,主要是起收敛作用的。
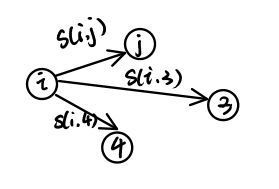
AP算法中在迭代的过程中对两种信息进行更新,可信度(Avaliability)和责任度(Responsibility)。更新公式为: r ( i , j ) = s ( i , j ) − m a x { a ( i , k ) + s ( i , k ) } k ∈ 1 , 2 , ⋯ , N a n d k ≠ j r(i,j) = s(i,j) - max\{a(i,k)+s(i,k)\}\quad k\in 1,2,\cdots,N and \quad k\ne j r(i,j)=s(i,j)−max{a(i,k)+s(i,k)}k∈1,2,⋯,Nandk̸=j a ( i , j ) = { m i n { 0 , r ( j , j ) + ∑ k { m a x ( 0 , r ( k , j ) ) } } k ∈ 1 , 2 , ⋯ , N , k ∉ ( i , j ) ∑ k { m a x ( 0 , r ( k , i ) ) } k ∈ 1 , 2 , ⋯ , N , k = i a(i,j)=\left\{ \begin{aligned} min\{0,r(j,j)+\sum_k\{max(0,r(k,j))\}\}\quad k\in 1,2,\cdots,N,k\notin (i,j)\\ \sum_k\{max(0,r(k,i))\}\quad \quad \quad \quad \quad k\in 1,2,\cdots,N,k=i\\ \end{aligned} \right. a(i,j)=⎩⎪⎪⎪⎨⎪⎪⎪⎧min{0,r(j,j)+k∑{max(0,r(k,j))}}k∈1,2,⋯,N,k∈/(i,j)k∑{max(0,r(k,i))}k∈1,2,⋯,N,k=i将AP算法模拟为一个选举的过程,假如网络中每个人都参与选举,选举目的是从所有参与选举的顶点中推荐出最合适的几个顶点作为代表。具体选举的过程描述如图所示:
--------------------------------------------
- 所有人都参加选举,参与选举的人既是选民也是候选人,并从中选出若干个作为代表。
- 相似性 s ( i , j ) s(i,j) s(i,j)可描述为选民i推荐候选人 j j j的一个偏好程度,也就是说 s ( i , j ) s(i,j) s(i,j)越大, i i i选择 j j j的可能性就越大。
- r ( i , j ) r(i,j) r(i,j)等于用 s ( i , j ) s(i,j) s(i,j)减去最强竞争者(候选人)的评分,可以理解为候选人 j j j对选民 i i i的吸引度, r ( i , j ) r(i,j) r(i,j)的更新过程对应选民 i i i对各个候选人的挑选,候选人越出众就越有吸引力。
- a ( i , j ) a(i,j) a(i,j)的更新过程对应候选人k的民意调查结果对选民i的影响。从公式中可以看出,责任度 r ( i , j ) > 0 r(i,j)>0 r(i,j)>0的值对可信度 a ( i , j ) a(i,j) a(i,j)都有正的加成。可以理解为很多人觉得候选 j j j不错,那么选民i也会觉得j不错。
- 对 r ( i , j ) r(i,j) r(i,j)和 a ( i , j ) a(i,j) a(i,j)交替更新的过程也就可以理解为选民在各个候选人之间不断的进行比较,不断的参考民意调查。
- 若最终选择出来的代表趋于稳定状态,则整个选举过程完成。
算法输入
- 顶点相似性
矩阵 S S S,可对称也可不对称,是待聚类数据集的相似性矩阵,可以用不同的方法进行计算,比如欧氏距离,Jaccard相似性,余弦相似性以及各种适用于不同应用场景的相似性等。 - 自我相似性
待聚类数据集中的数据点都是潜在的聚类中心,算法对潜在的聚类中心的描述主要表现在自我相似性 s ( i , i ) s(i, i) s(i,i)上.。
在初始状态的情况下数据集中每个数据点都是潜在的数据中心,所以在进行聚类之前,需要将 s ( i , i ) s(i, i) s(i,i)进行统一设置。从文献可知,可以将 s ( i , i ) s(i, i) s(i,i)设置成为相似性矩阵的中位数,或者平均值, s ( i , i ) s(i, i) s(i,i)的值的大小将会直接影响聚类结果数量,若 s ( i , i ) s(i, i) s(i,i)值越大,所有数据点都倾向于选择自己作为聚类中心,最终聚类数量就会越多,反之聚类数量越少。 - 阻尼因子 λ \lambda λ
算法在迭代更新可信度和责任度的过程中,还涉及了另外一个参数,叫做阻尼因子,用 λ \lambda λ来表示。该参数的作用是让AP算法能够快速收敛。阻尼因子的取值范围为0~1。AP算法的每次迭代过程中,λ作用于责任度和可信度,针对上一次迭代的责任度和可信度进行加权更新,更新规则如下: r n = ( 1 − λ ) × r n + λ × r n − 1 a n = ( 1 − λ ) × a n + λ × a n − 1 r_n = (1-\lambda)\times r_n + \lambda \times r_{n-1} \\ a_n = (1-\lambda)\times a_n + \lambda \times a_{n-1} rn=(1−λ)×rn+λ×rn−1an=(1−λ)×an+λ×an−1
结果的划分
1.聚类中心的选取
AP算法迭代完成后,首先需要确定数据集中所有的聚类中心。AP算法对聚类中心的判定主要参考责任度和可信度迭代更新完成后的值,判定为聚类中心的规则如公式4-5所示,即顶点i对自身的责任度和自身的可信度之和大于0时,则选择对应顶点作为聚类中心。
r ( i , i ) + a ( i , i ) > 0 ( 4 − 5 ) r(i,i)+a(i,i)>0 \quad \quad (4-5) r(i,i)+a(i,i)>0(4−5)
2.数据点与聚类中心之间的隶属关系
AP算法迭代完成后,若要获得对应的聚类结果,同样需要根据算法迭代完成后的责任度和可信度进行确认,选择聚类中心的规则如公式4-6所示,即选择与当前顶点i责任度与可信度之和最大的顶点j作为其聚类中心。
m a x { a ( i , j ) + r ( i , j ) } ( 4 − 6 ) max\{a(i,j)+r(i,j)\} \quad \quad (4-6) max{a(i,j)+r(i,j)}(4−6)
算法的流程
整个AP聚类的算法流程的描述如下:
- 初始化curIterNum, maxIterNum, a(i,k)=0, λ \lambda λ,δ=0,stableNum 【其中curIterNum表示当前已经迭代了的次数,maxIterNum表示算法最大迭代次数,λ为阻尼因子,默认为0.75,δ来记录聚类中心是否已经达到指定稳定次数stableNum 】
- 更新责任度r(i,j) r ( i , j ) = λ r ( i , j ) + ( 1 − λ ) ( s ( i , j ) − m a x { a ( i , k ) + s ( i , k ) } ) r(i,j) =\lambda r(i,j)+(1-\lambda)( s(i,j) - max\{a(i,k)+s(i,k)\}) r(i,j)=λr(i,j)+(1−λ)(s(i,j)−max{a(i,k)+s(i,k)})
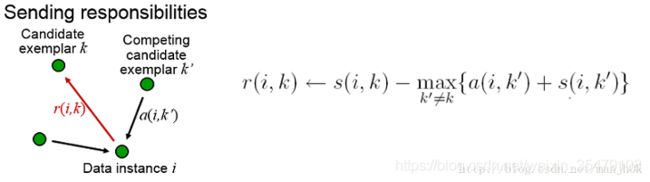
- 更新可信度a(i,j) a ( i , j ) = λ a ( i , j ) + ( 1 − λ ) m i n { 0 , r ( j , j ) + ∑ k { m a x ( 0 , r ( k , j ) ) } } i ≠ k a ( i , i ) = λ a ( i , i ) + ( 1 − λ ) ∑ k { m a x ( 0 , r ( k , j ) ) } j ≠ k , j ≠ i a(i,j) = \lambda a(i,j)+(1-\lambda)min\{0,r(j,j)+\sum_k\{max(0,r(k,j))\}\}\quad i\ne k \\ a(i,i) = \lambda a(i,i)+(1-\lambda)\sum_k\{max(0,r(k,j))\}\quad j\ne k,j\ne i a(i,j)=λa(i,j)+(1−λ)min{0,r(j,j)+k∑{max(0,r(k,j))}}i̸=ka(i,i)=λa(i,i)+(1−λ)k∑{max(0,r(k,j))}j̸=k,j̸=i
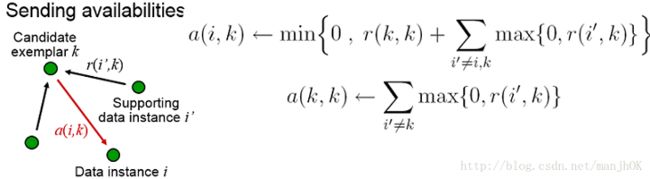
- 判断迭代是否稳定
根据公式4-6获取当前第t次迭代后聚类中心集合Et,如果Et=Et−1,则稳定次数δ加1,否则δ重置为0。若此时δ=stableNum则跳转至步骤6,否则跳转至步骤5 - curIterNum=curIterNum+1,若curIterNum=maxIterNum,则跳转至步骤6否则跳转至步骤2
- 从聚类结果中获取聚类中心,以及顶点之间的隶属关系
对500个随机生成的点进行聚类,复杂度是真的高。
简单实现:AP python简单实现
----------------------------------