牛顿法和高斯牛顿法对比

---

一、非线性最小二乘

考虑最小二乘函数F(x), 其等于：

通过求F(x)导数为零，获得x的最优值
求解这个非线性最小二乘的方法可以是牛顿法、高斯牛顿法、梯度下降法、列文伯格-马夸尔特法等

一、牛顿法

用目标函数的二阶泰勒展开近似该目标函数，通过求解这个二次函数的极小值来求解凸优化的搜索方向。

1、将F(x)在xk处进行泰勒展开，即：

此时，状态的更新式子为：

即此时求解的式子变为：

其中J为雅可比矩阵，即一阶导数矩阵
H为黑塞矩阵

通过求解上面线性方程，得到增量，叫牛顿法。
2、牛顿法具有超线性收敛性质，证明如下：
令

当获得最优值时，令导数为零，即

即

等式左右分别乘以

即

即

当

可得：

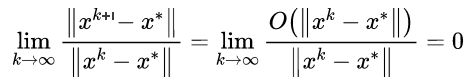
证毕

---

二、高斯牛顿法

高斯牛顿和牛顿法的区别在于牛顿法是对目标函数F二次偏导的迭代；高斯牛顿是分解目标函数F为f’*f后对f的一次偏导的迭代。
即此时不对F(x)展开，而是对f(x)展开，即




将上式变形为下面式子

可见和牛顿法获得了相同的等式形式。
但是此时H使用J^T * J近似；g = -J^T * f(x)
g函数是F(x)的一阶导数的转置，可见高斯牛顿和牛顿法的联系与区别

高斯牛顿方法虽然使用了雅可比矩阵乘积近似黑塞矩阵计算，但是雅可比矩阵乘积为奇异矩阵，此时会出现算法不收敛问题。

三、列文伯格-马夸尔特法（LM）

高斯牛顿法具有奇异性，即其可以在展开值附近有较好的优化结果，适合用于无约束优化。
LM针对高斯牛顿法的奇异性，增加了拉格朗日因子，保证了等式左边即HX始终正定。
此时优化问题变为

---

上式子的补充说明：
其中后面增加的那项就是通过拉格朗日乘子法，增加的拉格朗日因子约束。
拉格朗日乘子法是求优化函数f(x1,x2,x3,…,xn)在g(x1,x2,…xn)的约束条件下的极值方法。主要的思想是引入一个新的微小参数（拉格朗日乘子），将约束条件函数和原函数联系起来，使能配成与状态量数目相等的等式方程，保证等式的正定性。for an example:
对于优化函数f(x1,x2,x3,…,xn)的约束条件为A(x1,x2,x3,…,xn) = B;
设g(x1,x2,x3,…,xn)=B-A(x1,x2,x3,…,xn)
此时最小二乘优化函数变为

---

此时

变为

为简化计算，通常将D设为单位阵
其中H后面增加项（阻尼因子）会影响优化问题的梯度下降速度（收敛速度）。
如果阻尼因子较大，下降速度加快，如果阻尼因子减少，下降速度变慢。为了更好地选择这个阻尼因子，LM算法引入了比例因子，即：

也就是说比例因子等于（实际差值）/（近似差值）

其中比例因子分母始终大于0，如果：
比例因子小于0，那么表示F(X)递增，此时与我们设计思路违背，即不符。
马夸尔特设置了一个阻尼因子策略如下：

四、ceres求解优化问题

这里面的ceres::Solver::Options设置了非线性优化的求解器的以下设置，可以选择高斯牛顿或者LM等求解方法

//
// Created by xiang on 18-11-19.
//
 
#include 
#include 
#include 
#include 
 
using namespace std;
 
// 代价函数的计算模型
struct CURVE_FITTING_COST {
  CURVE_FITTING_COST(double x, double y) : _x(x), _y(y) {}
 
  // 残差的计算
  template<typename T>
  bool operator()(
    const T *const abc, // 模型参数，有3维
    T *residual) const {
    residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]); // y-exp(ax^2+bx+c)
    return true;
  }
 
  const double _x, _y;    // x,y数据
};
 
int main(int argc, char **argv) {
  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器
 
  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }
 
  double abc[3] = {ae, be, ce};
 
  // 构建最小二乘问题
  ceres::Problem problem;
  for (int i = 0; i < N; i++) {
    problem.AddResidualBlock(     // 向问题中添加误差项
      // 使用自动求导，模板参数：误差类型，输出维度，输入维度，维数要与前面struct中一致
      new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
        new CURVE_FITTING_COST(x_data[i], y_data[i])
      ),
      nullptr,            // 核函数，这里不使用，为空
      abc                 // 待估计参数
    );
  }
 
  // 配置求解器
  ceres::Solver::Options options;     // 这里有很多配置项可以填
  options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;  // 增量方程如何求解
  options.minimizer_progress_to_stdout = true;   // 输出到cout
 
  ceres::Solver::Summary summary;                // 优化信息
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  ceres::Solve(options, &problem, &summary);  // 开始优化
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
 
  // 输出结果
  cout << summary.BriefReport() << endl;
  cout << "estimated a,b,c = ";
  for (auto a:abc) cout << a << " ";
  cout << endl;
 
  return 0;
}