超几何分布HyperGeometricDistribution
文章目录
- 超几何分布HyperGeometricDistribution
- 举例并图示
- 大数据集情况
超几何分布HyperGeometricDistribution
超几何分布描述不放回抽样的抽取试验,即每进行一次抽样,事件发生的概率均有一定的变化。
如:
在含有M个红球的N个球中,任取n个球,其中恰有X个红球,则事件{X=k}发生的概率为:
P ( X = k , n , M , N ) = C M k C N − M n − k C N n \large\displaystyle P(X=k,n,M,N)=\frac{C_M^kC_{N-M}^{n-k}}{C_N^n} P(X=k,n,M,N)=CNnCMkCN−Mn−k
如果是抽取 n + 1 n+1 n+1个球,则
P ( X = k , n + 1 , M , N ) = C M k C N − M n + 1 − k C N n + 1 \large\displaystyle P(X=k,n+1,M,N)=\frac{C_M^kC_{N-M}^{n+1-k}}{C_N^{n+1}} P(X=k,n+1,M,N)=CNn+1CMkCN−Mn+1−k
期望:
E ( X ) = ∑ x = 0 n x P ( X = x ) = ∑ x = 0 n x C M k C N − M n − k C N n = n M N ∑ C M − 1 k − 1 C N − M n − ( k − 1 ) C N − 1 n − 1 = n M N \begin{aligned}\Large\displaystyle E(X) &=\sum_{x=0}^{n}xP(X=x)=\sum_{x=0}^{n}x\frac{C_M^kC_{N-M}^{n-k}}{C_N^n}\\ \Large\displaystyle &=n\frac{M}{N}\sum\frac{C_{M-1}^{k-1}C_{N-M}^{n-(k-1)}}{C_{N-1}^{n-1}} \\ &=n\frac{M}{N}\end{aligned} E(X)=x=0∑nxP(X=x)=x=0∑nxCNnCMkCN−Mn−k=nNM∑CN−1n−1CM−1k−1CN−Mn−(k−1)=nNM
方差
V a r ( X ) = E [ ( X − E ( X ) ) 2 ] = n M ( N − M ) ( N − n ) N 2 ( N − 1 ) \displaystyle Var(X)=E[(X-E(X))^2]=n\frac{M(N-M)(N-n)}{N^2(N-1)} Var(X)=E[(X−E(X))2]=nN2(N−1)M(N−M)(N−n)
举例并图示
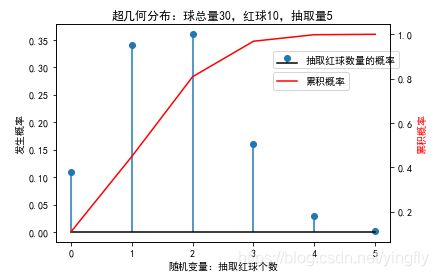
从含有10个红球的30个球中抽取5个球,则红球个数的概率符合超几何分布。
from scipy import stats
N = 30 # total number of the objects
M = 10 # total number of Type I objects
n=5
# scipy 超几何分布函数的参数顺序是 (总量,类别量,抽取量)
po=stats.hypergeom(N,M,n)
x=np.arange(n+1)
px=po.pmf(x)
# 图形
fig = plt.figure()
ax = plt.gca()
line1 = ax.stem(x,px,basefmt='k',label='抽取红球数量的概率');
ax.set_xlabel('随机变量:抽取红球个数');
ax.set_ylabel('发生概率');
ax.set_title('超几何分布:球总量30,红球10,抽取量5');
ax2=plt.twinx()
y=po.cdf(x)
line2 = ax2.plot(x,y,'r',label='累积概率')
ax2.set_ylabel('累积概率',color='r')
ax.legend(loc=(0.65,0.8));
ax2.legend(loc=(0.65,0.7))
# 统计量期望、方差
po.stats()
#输出为
(array(1.66666667), array(0.95785441))
E ( x ) = 5 × 10 30 = 5 / 3 E(x)=5×\frac{10}{30}=5/3 E(x)=5×3010=5/3
如果猜测红球个数输赢,即 P ( X = r ) > 0.5 P(X=r)>0.5 P(X=r)>0.5,则
po.ppf(0.5)
输出为2.0.
大数据集情况
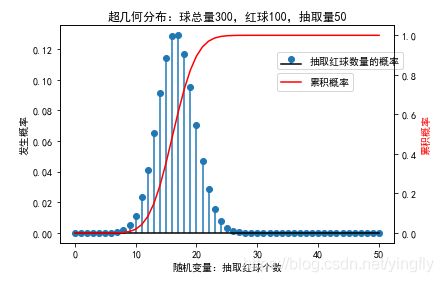
从含有100个红球的300个球中抽取50个球,则红球个数的概率符合超几何分布,接近正态分布。
N = 300 # total number of the objects
M = 100 # total number of Type I objects
n=50
po=stats.hypergeom(N,M,n)
x=np.arange(n+1)
px=po.pmf(x)
# 图形
fig = plt.figure()
ax = plt.gca()
line1 = ax.stem(x,px,basefmt='k',label='抽取红球数量的概率');
ax.set_xlabel('随机变量:抽取红球个数');
ax.set_ylabel('发生概率');
ax.set_title('超几何分布:球总量300,红球100,抽取量50');
ax2=plt.twinx()
y=po.cdf(x)
line2 = ax2.plot(x,y,'r',label='累积概率')
ax2.set_ylabel('累积概率',color='r')
ax.legend(loc=(0.65,0.8));
ax2.legend(loc=(0.65,0.7))