操龙兵：非独立同分布学习

原文地址：非独立同分布

AIDL简介

     “人工智能前沿讲习班”（AIDL）由中国人工智能学会主办，旨在短时间内集中学习某一领域的基础理论、最新进展和落地方向，并促进产、学、研相关从业人员的相互交流，对于硕士、博士、青年教师、企事业单位相关从业者、预期转行AI领域的爱好者均具有重要的意义。2018年AIDL活动正在筹备，敬请关注获取最新消息。

导读

在第三届“人工智能前沿讲习班”上，悉尼科技大学的操龙兵教授做了题为《非独立同分布学习》的报告【1】。报告介绍了非独立同分布学习的概念、非独立同分布性、耦合学习、以及非独立同分布学习在聚类、异常检测、推荐系统等方法的一些初步结果，以及非独立同分布学习的研究挑战、一些思考等。非独立同分布学习是数据科学、大数据分析以及企业数据分析应用中可能无法避开的基本学习问题。本文根据操龙兵教授当日报告内容整理发布，对于相关领域的研究工作具有长期价值。

关注本公众号，回复“操龙兵”，获取完整版PPT

分享PPT仅供学习交流，请勿外传

讲师简介

操龙兵，悉尼科技大学工程与信息技术学院教授。主要研究方向包括行为信息学（BehaviorInformatics）、非独立同分布学习（Non-IID  Learning）、决策知识发现（Actionable  Knowledge Discovery），以及数据挖掘、机器学习、人工智能与智能系统等领域中一些普遍关注的问题。他在上述方向发表专著3部、论文300余篇。他比较早地在国际上推动数据科学与分析学的产、学、研工作。在2007年成立澳洲第一个数据科学与知识发现实验室；2011创立世界上第一个分析学（Analytics）研究硕士学位与博士学位；2011所创立的先进分析研究所是澳洲政府发布的关于大数据策略与更好的大数据实践等白皮书中唯一一个被特别介绍的机构；2015年在Springer创立International  Journal of Data Science and Analytics。他是KDD2015等多个大会主席或程序委员会主席。在大数据分析应用方面，与诸多政府、大型企业、国际知名运营商等的合作支持，直接领导与实施的项目涉及金融与资本市场监管与投资，金融危机与跨市场研究，财政、社保、医保、税务、统计、审计、知识产权等政府业务风控，电商与零售分析，反洗钱、网银与支票风控，寿险与车险风控，航空常旅客管理，电信经营分析决策，教育与学习行为分析与管理，以及出版等多个行业。所领导的大数据分析项目已为相关政府与企业创作数十亿澳元的直接经济效益、在相关媒体、政府与经合组织等报告中被提及。

Progress Review: Non-IID Learning

大数据分析（big data analytics）就像是“盲人摸象”，要解决的问题是如何让“盲人”识别“象”，不管“象”大还是小。我们分析很多数据时会面临这种“we don’t know what we don’t know”的问题，其中一个最基本的问题可能就是学习问题所基于的基本假设，其中之一就是独立同分布假设（independent and identically distributed - IID）。

实际的问题与数据一般可能都是非独立同分布的（Non-IID），数据具有非独立同分布性（Non-IIDness）。分析非独立同分布数据的学习理论与方法称之为非独立同分布学习（Non-IID Learning）【1, 2, 3】。

由于时间关系，这里只能简单介绍我们在非独立同分布学习方面的某些研究进展，特别侧重概念与思想方面。实际上，我们的研究包括非独立同分布性的基本概念，数据表达，数据离散化，对包括K-Means、Spectral Clustering、KNN、Decision Tree等基于IID假设的经典算法的改进，研究Non-IID集成学习、图像处理、计算机视觉、统计机器学习、模式发现、推荐系统、文本分析、关键词查询等【3】。非独立同分布学习涉及经典学习理论的各个方面，个人认为很多原有的基于独立同分布假设的学习理论与方法都可能需要重新思考，特别是在出来多源异构数据时，是不可回避的根本问题。面向实际问题与数据的分析与学习理论与方法需要更针对实际问题和实际数据的特点与复杂性。

IIDness / IID Learning

一般的学习问题或分析问题可以抽象成上图左侧的描述。外圈虚线是学习问题的边界，不同形状颜色的图形代表不同类型的对象或数据源，彼此的连线反映了它们之间的关系。一般的学习基于IID假设，转换为右侧图示，O1~O3三个对象被认为是同分布的，且相互独立。之后构建目标函数。以O3为例，参考O3和基准O （benchmark）之间的关系计算距离或相似度d，再通过目标函数检测其与O1或O2是不是同一类、群、模式，或是不是异常。

如图是一个股票交易数据的例子，对其进行K-Means或Fuzzy C-Means聚类。有时效果不好，可能的原因是这些方法基于IID假设，但实际对象间存在关系，此外数据分布的异构性、学习的目标、均值的设置等也有所影响。对于Decision Tree等一些分类算法，如果数据不满足IID假设，结果也会存在问题。

简言之，利用基于IID假设的独立同分布学习算法在Non-IID数据上学习，得到的结果可能不完整、有偏差，甚至是错误的。

Non-IIDness / Non-IID Learning Concepts

下面介绍非独立同分布性Non-IIDness的概念【2】。不论是大数据还是小数据都有两个问题：一个是异构性（Heterogeneity），体现在很多方面，比如数据的类型、属性、数据源、关注的数据的方面，还包括数据的模式、结构、分布、关系，甚至学习结果也可能是异构的；另一个问题是Coupling Relationships，它不一定就是dependence、association或correlation，而是涉及到很多方面，有比较复杂的关系、层次、类型等。这两方面结合起来，就是非独立同分布性（Non-IIDness）。

从一个例子来理解Coupling Relationships。如上图，一个人的不同行为behavior1、behavior2之间存在关系，关系可能有很多种，比如Temporal Relation、Inferential Relation、Party-based Relation。我们需要研究如何将这些复杂的显式或者隐式的关系表达出来。

Non-IID的基本思想是，对于一个学习问题，要尊重其原本特点与复杂性，原来的异构要保持，原来的关系也要充分学习、表达出来。比如判断图中O3是哪个模式、群、类或是不是异常时，要考虑O3是否受O1或O2的影响，因此计算d3要考虑r13和r23。寻找O点（benchmark）时，也要考虑它会受到d1、d2影响。这两方面结合起来，目标函数就非常复杂了。以上就是对Non-IID学习高度抽象的一种表达。

Coupling Learningand Non-IID Categorical Clustering

首先介绍非独立同分布学习中的Coupling Learning（耦合学习）【3】的概念与方法，我们结合K-Modes聚类法进行介绍【4】。

非独立同分布学习需要建立在一个比较合适的数据结构上。如果数据能够用信息表来表达，可以作为一种研究非独立同分布学习的基本数据结构。

信息表里有O1到ON多个对象，有很多属性来描述这些对象，后面的M1到MQ可能是多个方法，或者是multi-view、multi-task、multi-label等，构成一个扩展信息表，表示一个学习问题所涉及的数据、方法与结果。对扩展信息表进行分析，比如在A2列，假设A2属性是性别，把每个对象的属性值标出来（V12, V22,…,VN2），考虑这些属性值之间的关系（称为属性值耦合关系，intra-attribute couplings），同时也要考虑该属性受其他属性A1,…, AJ等的影响，比如年龄、工作性质、兴趣等，称之为属性间耦合关系（inter-attribute couplings）。进一步计算对象间（比如O1, O2等）相似性时就需要把属性内与属性间的耦合关系综合起来。有时候这些耦合关系会比较弱，有时候关系会比较强。对于多方法M1到MQ，也要考虑基于每个方法的结果之间的关系，以及它们与属性耦合的关系。

对每个对象进行学习的时候，要进行层次性的思考，从每个属性到不同属性的交互，再到多方法、多数据源等。这些方面考虑得比较周到，对对象进行分类、聚类或异常检测等学习与分析时才比较准。这是一个基本的框架，下面讨论这些层次化耦合学习的一个具体例子。

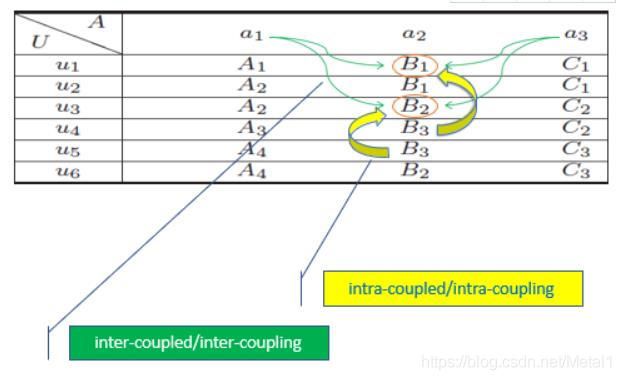
首先构建一个信息表，u是不同的人，有性别、年龄、工作性质等属性。为了学习层次化的耦合关系，这里提出两个概念，一个是属性内部关系，一个是属性间的关系。比如对属性a2，u1和u3的值分别为B1和B2，B1和B2之间的关系就是intra-attribute coupling关系，或者称为属性内耦合关系。研究B1和B2之间的关系时也要考虑a1和a3属性对它的影响，就是inter-attribute coupling即属性间耦合关系。

表达这些概念需要建立信息函数（information function），从表中将信息提取出来。f函数和f*函数用于提取给定对象在某属性上的值的信息，g函数和g*函数用于提取给定属性值的对象的信息。这样会形成很多集合，集合之间具有关系。

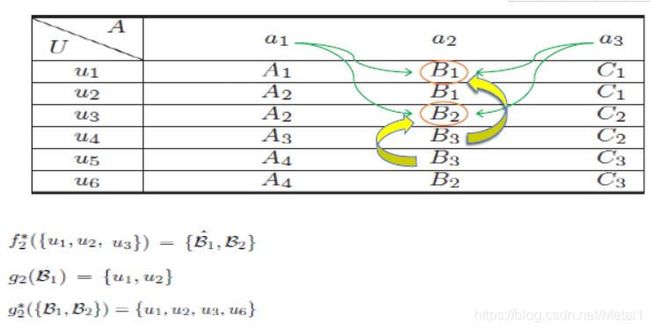
如图，根据信息函数f*可以知道u1、u2、u3三个对象在a2属性上的值是B1、B2，其中B1可能出现多次，所以不仅要确定这个值，还要考虑它多次出现的情况。通过函数g确定a2属性值为B1时有对象u1、u2。给定多个值时，g*函数将所有对象找出。

进一步考虑一个属性上的值之间的关系如何建模。参考公式4.1，考虑两方面，一方面是，表达x、y两个值在j属性上的相似度。另一方面也要考虑j属性上x、y的相似度受到其他属性的影响，多个属性的影响叠加得到。两方面结合才能反映属性值x、y在这个信息表中可能的相似性。考虑对象间的相似性，需要将所有属性的相似性叠加得到对象间的耦合属性的相似性度量CASO（Coupled Attribute Similarity for Objects），进一步也可以得到对象间的耦合属性的相异性度量CADO（Coupled Attribute Dissimilarity for Objects）。

上述相似性度量可以灌入像K-Modes的聚类算法中对这些算法进行改进与更好地捕获数据中存在的层次化的耦合关系。比如，在UCI数据集上用RD、DI、DBI、SD等聚类算法评价指标将我们的相似性度量CADO和常用的SMD、OFD、ADD等方法进行比较，可以看出在一些数据集上我们的方法有明显优势，而在比较简单的数据集上相差不大。