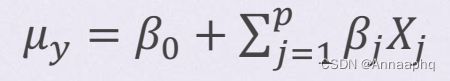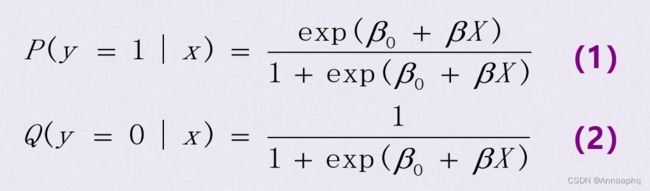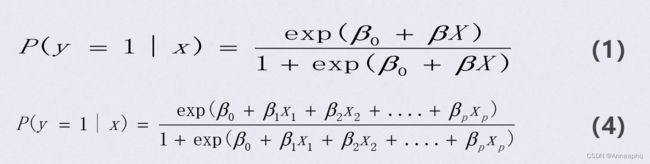R之广义线性模型

R之广义线性模型

一、广义线性模型和glm()函数

• 结果变量是类别型的。二值变量（比如：是/否、有效/无效、活着/死亡）和多分类变量（比如差/良好/优秀）都显然不是正态分布；
• 结果变量是计数型的。（比如，一年内哮喘发生的次数，一生中流产的次数，一周交通事故的数目，每日酒水消耗的数量）。这类变量都是非负有限值，而且它们的均值和方差通常都是相关的（正态分布变量间不是如此，而是相互独立）；
• 广义线性模型扩展了线性模型的框架，它包含了非正态因变量的分析。

1、标准线性模型公式

现要对响应变量Y和p个预测变量X1…Xp间的关系进行建模。在标准线性模型中，可假设Y呈正态分布，关系的形式为：

该等式表明响应变量的条件均值是预测变量的线性组合。参数βj指一单位Xj的变化造成的Y预期的变化， β0指当所有预测变量都为0时Y的预期值。对于该等式，你可通俗地理解为：给定一系列X变量的值，赋予X变量合适的权重，然后将它们加起来，便可预测Y观测值分布的均值。

2、广义线性模型公式

上使中并没有对预测变量Xj做任何分布的假设。与Y不同，它们不需要呈正态分布。实际上，它们常为类别型变量（比如方差分析设计）。另外，对预测变量使用非线性函数也是允许的，比如你常会使用预测变量X2或者X1×X2，只要等式的参数（β0, β1, …, βp）为线性即可。广义线性模型公式为：

其中g(μY)是条件均值的函数（称为连接函数）。另外，你可放松Y为正态分布的假设，改为Y服从指数分布族中的一种分布即可。设定好连接函数和概率分布后，便可以通过最大似然估计的多次迭代推导出各参数值。

3、glm()函数

R中可通过glm()函数（还可用其他专门的函数）拟合广义线性模型。它的形式与lm()类似，只是多了一些参数。函数的基本形式为：

glm(formula, family=family(link=function), data=) 

表中列出了概率分布（family）和相应默认的连接函数（function）

4、lm()与glm()函数

标准线性模型也是广义线性模型的一个特例。如果令连接函数g(μY)=μY或恒等函数，并设定概率分布为正态（高斯）分布，那么：

glm(Y~X1+X2+X3, family=gaussian(link="identity"), data=mydata)

生成的结果与下列代码的结果相同：

lm(Y~X1+X2+X3, data=mydata) 

5、logistic回归模型

这也是广义线性模型中的一种

Logistic回归适用于二值响应变量（0和1），但rms包中可以进行等级资料回归。模型假设Y服从二项分布，线性模型的拟合形式为：

其中π=μY是Y的条件均值（即给定一系列X的值时Y=1的概率）， (π/1–π)为Y=1时的优势比， log(π/1–π)为对数优势比，或logit。本例中， log(π/1–π)为连接函数，概率分布为二项分布，可用如下代码拟合Logistic回归模型：

glm(Y~X1+X2+X3, family=binomial(link="logit"), data=mydata) 
#假设有一个响应变量（Y）、三个预测变量（X1、 X2、 X3）和一个包含数据的数据框（mydata）

6、泊松回归模型

这也是广义线性模型中的一种

泊松回归适用于在给定时间内响应变量为事件发生数目的情形。它假设Y服从泊松分布，线性模型的拟合形式为：

其中λ是Y的均值（也等于方差）。此时，连接函数为log(λ)，概率分布为泊松分布，可用如下代码拟合泊松回归模型：

glm(Y~X1+X2+X3, family=poisson(link="log"), data=mydata) 

7、可连用的函数

与分析标准线性模型时lm()连用的许多函数在glm()中都有对应的形式，其中一些常见的函数如下：

• summary() 展示拟合模型的细节
• coefficients()、 coef() 列出拟合模型的参数（截距项和斜率）
• confint() 给出模型参数的置信区间（默认为95%）
• residuals() 列出拟合模型的残差值
• anova() 生成两个拟合模型的方差分析表
• plot() 生成评价拟合模型的诊断图
• predict() 用拟合模型对新数据集进行预测
• deviance() 拟合模型的偏差
• df.residual() 拟合模型的残差自由度

8、模型拟合和回归诊断

当评价模型的适用性时，你可以绘制初始响应变量的预测值与残差的图形

plot(predict(model, type="response"),residuals(model, type= "deviance"))

R可列出帽子值（hat value）、学生化残差值和Cook距离统计量的近似值。

plot(hatvalues(model))
plot(rstudent(model))
plot(cooks.distance(model))

还可以用其他方法，创建一个综合性的诊断图。在后面的图形中，横轴代表杠杆值，纵轴代表学生化残差值，而绘制的符号大小与Cook距离大小成正比。

library(car)
influencePlot(model) 

二、logistic回归模型

1、logistic回归模型概述

Logistic回归模型是一种概率模型，它是以某一事件发生与否的概率P为因变量，以影响P的因素为自变量建立的回归模型，分析某事件发生的概率与自变量之间的关系，是一种非线性回归模型

适用的资料类型：适用于因变量为二项或多项分类（有序、无序）的资料

2、logistic回归模型分类

条件logistic回归模型：适合于配对或配伍设计资料；

非条件logistic回归模型：适合于成组设计的统计资料；

**因变量可以是：**两项分类、无序多项分类、有序多项分类等

3、logistic回归模型结构

Logistic分布函数表达：

Y 的取值在－ ∞～＋ ∞之间，函数值F(y) 在0～ 1之间取值，且呈单调上升的S型曲线。可以将这一特征运用到临床医学和流行病学中描述事件发生的概率与影响因素的关系

logistic分布函数

logistic回归模型方程

利用Logistic分布函数的特征来表示在自变量X的作用下出现阳性结果或阴性结果的概率

阳性结果的概率记为： P( y=1|x)，（在X 作用下，出现Y=1的概率）

出现阴性结果的概率为: Q( y=0|x), （在X 作用下，出现Y=0的概率）

注意： P+Q=1

4、只有一个自变量时，Logistic回归模型

式中， β0为回归线的截距， β是与X有关的参数，称回归系数

注意： P/Q称为事件的优势，流行病学中称为比值(odds)

5、多个自变量时，Logistic回归模型

不同自变量个数对比：

6、logit变换：将S型曲线转化为直线

其实变换之后这就是所谓的线性回归方程：

• ln(P/Q)称为 logit§变换；
• P/Q称为事件的优势，流行病学中称为比值(odds)

因此，优势的对数值与影响因素之间呈线性关系

比值比 或 优势比(odds ratio), 简记为 OR

暴露组的优势（比值）与非暴露组的优势（比值）之比，称优势比（比值比）（OR）。 OR用于说明暴露某因素引起疾病或死亡的危险度大小。

7、案例1

以AER包中的数据框Affairs为例，我们将通过探究婚外情的数据来阐述Logistic回归分析的过程。首次使用该数据前，请确保已下载和安装了此软件包（使用install.packages(“AER”)）

婚外情数据取自1969年（Psychology Today）所做一个非常有代表性的调查。该数据从601个参与者收集了9个变量，包括一年来婚外私通的频率以及参与者性别、年龄、婚龄、是否有小孩、宗教信仰程度（5分制， 1分表示反对， 5分表示非常信仰）、学历、职业（逆向编号的戈登7种分类），还有对婚姻自我评分（5分制， 1表示非常不幸福， 5表示非常幸福）

Affairs$ynaffair[Affairs$affairs > 0] <- 1 #有就是1
Affairs$ynaffair[Affairs$affairs == 0] <- 0
Affairs$ynaffair <- factor(Affairs$ynaffair, 
                           levels=c(0,1),
                           labels=c("No","Yes"))
table(Affairs$ynaffair)

# fit full model
fit.full <- glm(ynaffair ~ gender + age + yearsmarried + children + 
                  religiousness + education + occupation +rating,
                data=Affairs,family=binomial())
summary(fit.full)

fit.reduced <- glm(ynaffair ~ age + yearsmarried + religiousness + 
                     rating, data=Affairs, family=binomial())
summary(fit.reduced)

# compare models
anova(fit.reduced, fit.full, test="Chisq")

coef(fit.reduced)
exp(coef(fit.reduced)) #算OR值
confint(fit.reduced) #算OR值
exp(-0.07006400)#算OR值的95%CI，把上步计算出的的值取反对数

是否还要其他解决思路？

在婚外情的例子中，婚外偷腥的次数被二值化为一个“是/否”的响应变量，这是因为我们最感兴趣的是在过去一年中调查对象是否有过一次婚外情。如果兴趣转移到量上（过去一年中婚外情的次数），便可直接对计数型数据进行分析。分析计数型数据的一种流行方法是泊松回归

想看评分对婚外情的影响：

testdata <- data.frame(rating = c(1, 2, 3, 4, 5),
                       age = mean(Affairs$age),
                       yearsmarried = mean(Affairs$yearsmarried),
                       religiousness = mean(Affairs$religiousness)) #其余变量取均值
testdata$prob <- predict(fit.reduced, newdata=testdata, type="response")
testdata

看年龄对婚外情影响：

testdata <- data.frame(rating = mean(Affairs$rating),
                       age = seq(17, 57, 10), 
                       yearsmarried = mean(Affairs$yearsmarried),
                       religiousness = mean(Affairs$religiousness))
testdata$prob <- predict(fit.reduced, newdata=testdata, type="response")
testdata

这里还有一段不是太明白，如果有大佬指点一下非常感激：

fit <- glm(ynaffair ~ age + yearsmarried + religiousness +
             rating, family = binomial(), data = Affairs)
fit.od <- glm(ynaffair ~ age + yearsmarried + religiousness +
                rating, family = quasibinomial(), data = Affairs)
pchisq(summary(fit.od)$dispersion * fit$df.residual,  
       fit$df.residual, lower = F)

7.1变量筛选方式

• 用Enter法把所有自变量全纳入（不做筛选）
• 用逐步回归筛选自变量（SPSS软件包括6种筛选方式）
• 先做单因素Logistic回归， p<0.1纳入最后的回归方程

最终筛选出影响新生儿体重的独立影响因素

8、案例2

表11-5 是一个研究吸烟、饮酒与食管癌关系的病例-对照研究资料，试作Logistic 回归分析。设y=1 表示患有食管癌， y=0 表示未患食管癌。令x1=1 表示吸烟， x1=0 表示不吸烟: x2=1表示饮酒， x2=0 表示不饮酒

Example11_4  <- read.table ("example11_4.csv", header=TRUE, sep=",")
attach(Example11_4)

fit1 <- glm(y~ x1 + x2, family= binomial(), data=Example11_4)
summary(fit1)
coefficients(fit1)
exp(coefficients(fit1))
exp (confint(fit1)) #默认赋值大的与赋值小的相比

fit2 <- glm(y~ x1 + x2 + x1:x2 ,  family= binomial(), data=Example11_4)
summary(fit2)
coefficients(fit2)
exp(coefficients(fit2))
exp (confint(fit2))

若想探究吸烟与饮酒的交互作用：

本例分析吸烟、饮酒危险因素对患食管癌的影响程度以及它们的交互影响程度。设y=1 表示患有食管癌， y=0 表示未患食管癌。令x1=1 表示吸烟， x1=0 表示不吸烟: x2=1表示饮酒， X2=0 表示不饮酒。这样， x1和x2的交叉水平有4 个，建立4 个哑变量分别代表这4 个水平，记为x11、 x10 、 x01、 x00，它们表示4 种不同的生活方式，即x11表示既吸烟又饮酒， X10表示吸烟但不饮酒， x01 表示不吸烟但饮酒， x00表示既不吸烟又不饮酒。将前3 个哑变量放进模型， 则可得到前3 种生活方式相对于最后一种生活方式患食管癌的相对危险度。

Example11_4$x11  <- ifelse (x1==1 & x2==1, 1, 0)
Example11_4$x10  <- ifelse (x1==1 & x2==0, 1, 0)
Example11_4$x01  <- ifelse (x1==0 & x2==1, 1, 0)
Example11_4$x00  <- ifelse (x1==0 & x2==0, 1, 0)

fit3 <- glm(y~ x11 + x10 + x01, family= binomial(), data=Example11_4)
summary(fit3)
coefficients(fit3)
exp(coefficients(fit3))
exp(confint(fit3))
detach (Example11_4)

9、案例3

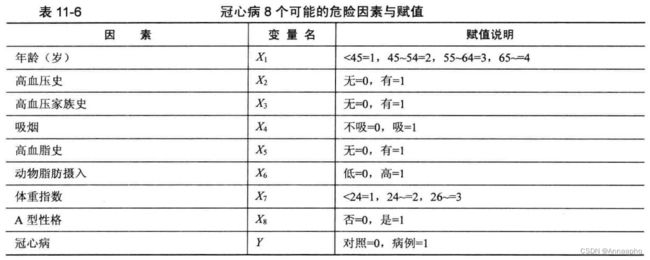
例11-5 为了探讨冠心病发生的有关危险因素， 对26例冠心病病人和28例对照者进行病例-对照研究，各因素的说明及资料见表11-6 和表11-7 。试用Logistic逐步回归分析方法筛选危险因素。

Example11_5 <- read.table ("example11_5.csv", header=TRUE, sep=",")
attach(Example11_5)
fullfit <- glm(y~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 ,  family= binomial(), data=Example11_5)
summary(fullfit)
nothing <- glm(y~ 1, family= binomial(), data=Example11_5)#建立一个空模型
summary(nothing)
bothways <- step(nothing, list(lower=formula(nothing), upper=formula(fullfit)),  direction="both")
fit1 <- glm(y~ x6 + x5 + x8 + x1 + x2 ,  family= binomial(), data=Example11_5)#逐步法找到的最优选择
summary(fit1)
fit2 <- glm(y~ x6 + x5 + x8 + x1, family= binomial(), data=Example11_5)
summary(fit2)
coefficients(fit2)
exp(coefficients(fit2))
exp (confint(fit2))
detach (Example11_5)

10、案例4

例11-6 某研究机构为了研究胃癌与饮酒的相关关系，收集了病例对照资料如表11-9 所示，其中D 和D’ 分别表示患有胃癌和未患有胃癌， E 和E’ 分别表示饮酒和不饮酒。试用条件Logistic回归模型分析饮酒对胃癌的影响。

本例是一个配对资料

#install.packages("survival")
library(survival)
Example11_6  <- read.table ("example11_6.csv", header=TRUE, sep=",")
attach(Example11_6)
model <- clogit(outcome~ exposure+ strata(id)) #strata指对子号
summary(model)
detach(Example11_6)

11、R中扩展的Logistic回归及其变种

稳健Logistic回归 robust包中的glmRob()函数可用来拟合稳健的广义线性模型，包括稳健Logistic回归。当拟合Logistic回归模型数据出现离群点和强影响点时，稳健Logistic回归便可派上用场。

多项分布回归 若响应变量包含两个以上的无序类别（比如，已婚/寡居/离婚），便可使用mlogit包中的mlogit()函数拟合多项Logistic回归。

序数Logistic回归 若响应变量是一组有序的类别（比如，信用风险为差/良/好），便可使用rms包中的lrm()函数拟合序数Logistic回归

三、logistic回归模型列线图绘制

1、临床预测模型的本质

科研预测模型是通过已知来预测未知，而模型就是一个复杂的公式。也就是把已知的东西通过这个模型的计算来预测未知的东西。

临床预测模型的本质就是通过回归建模分析，回归的本质就是发现规律。回归是量化刻画， X多大程度上影响Y。尤其是多元线性、 Logistic、 Cox回归分析等。

模型的验证也体现着较高技术难度。模型效能评价是统计分析、数据建模、课题设计的关键所在。2、

2、临床预测模型验证步骤

3、临床预测模型类研究思路

举一个例子：

临床上有多个心血管疾病风险预测工具： Framingham、 QRISK、 PROCAM、ASSIGN评分。 Heart发表综述《Graphics and Statistics for Cardiology:Clinical Prediction Rules》 以心血管风险评分(CVD risk factor)为例探讨如何借助图形优势构建疾病的预测模型，并提出了6个重要步骤 ：

1. 选择一组预测变量作为潜在CVD影响因素纳入到风险评分中
2. 选择一个合适的统计模型来分析预测变量和CVD之间的关系
3. 从已有的预测变量中，选择足够重要的变量纳入到风险评分中构造风险评分模型
4. 评价风险评分模型
5. 在临床实践中解释风险评分的使用。

4、TRIPOD声明: 临床预测模型分类

• 既往没有模型：为了解决一个全新的问题，展示自己好也就够了
• 既往已有模型：评价这两个模型的优劣
• 改进现有的模型：增加其他预测指标或更新现有指标

5、列线图案例1

还是上方的案例

library(foreign) 
library(rms)

mydata<-read.spss("lweight.sav")
mydata<-as.data.frame(mydata) #转成数据框结构
head(mydata)

mydata$low <- ifelse(mydata$low =="低出生体重",1,0)
mydata$race1 <- ifelse(mydata$race =="白种人",1,0)
mydata$race2 <- ifelse(mydata$race =="黑种人",1,0)
mydata$race3 <- ifelse(mydata$race =="其他种族",1,0)

attach(mydata)
dd<-datadist(mydata) #打包数据集
options(datadist='dd')

fit1<-lrm(low~age+ftv+ht+lwt+ptl+smoke+ui+race1+race2,data=mydata,x=T,y=T)
fit1
summary(fit1)
nom1 <- nomogram(fit1, fun=plogis,fun.at=c(.001, .01, .05, seq(.1,.9, by=.1), .95, .99, .999),lp=F, funlabel="Low weight rate")#画列线图
plot(nom1)
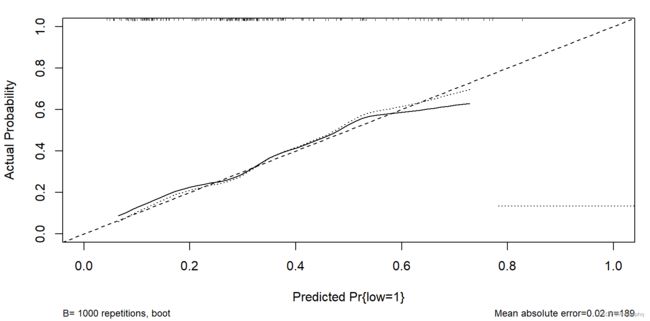
cal1 <- calibrate(fit1, method='boot', B=1000)
plot(cal1,xlim=c(0,1.0),ylim=c(0,1.0))

列线图的解读：每个变量对应分值相加后，总分值对应最下面的比例，就是发生概率

如果把种族因子化：

mydata$race <- as.factor(ifelse(mydata$race=="白种人", "白种人","黑人及其他种族"))

dd<-datadist(mydata)
options(datadist='dd')

fit2<-lrm(low~age+ftv+ht+lwt+ptl+smoke+ui+race,data=mydata,x=T,y=T)
fit2
summary(fit2)

nom2 <- nomogram(fit2, fun=plogis,fun.at=c(.001, .01, .05, seq(.1,.9, by=.1), .95, .99, .999),lp=F, funlabel="Low weight rate")
plot(nom2)
cal2 <- calibrate(fit2, method='boot', B=1000)
plot(cal2,xlim=c(0,1.0),ylim=c(0,1.0))

把筛选出的变量再拟合一个模型：

fit3<-lrm(low~ht+lwt+ptl+smoke+race,data=mydata,x=T,y=T)
fit3
summary(fit3)

nom3 <- nomogram(fit3, fun=plogis,fun.at=c(.001, .01, .05, seq(.1,.9, by=.1), .95, .99, .999),lp=F, funlabel="Low weight rate")
plot(nom3)
cal3 <- calibrate(fit3, method='boot', B=1000)#画校正曲线
plot(cal3,xlim=c(0,1.0),ylim=c(0,1.0))

四、logistic回归模型：C-Statistics 计算

R中如何计算C-Statistics

• rms包中lrm函数拟合logistic回归模型，模型参数可直接读取C， Dxy
• ROCR包中performance函数计算AUC
• Hmisc包中的somers2函数直接计算C, Dxy

library(foreign) 
library(rms)

mydata<-read.spss("lweight.sav")
mydata<-as.data.frame(mydata)#变成数据框格式
head(mydata)

mydata$low <- ifelse(mydata$low =="低出生体重",1,0) #设置哑变量
mydata$race1 <- ifelse(mydata$race =="白种人",1,0)
mydata$race2 <- ifelse(mydata$race =="黑种人",1,0)
mydata$race3 <- ifelse(mydata$race =="其他种族",1,0)

attach(mydata)
dd<-datadist(mydata) #打包数据
options(datadist='dd')

fit1<-lrm(low~age+ftv+ht+lwt+ptl+smoke+ui+race1+race2,data=mydata,x=T,y=T)
fit1 #直接读取模型中Rank Discrim.参数 C

mydata$predvalue<-predict(fit1)
library(ROCR)
pred <- prediction(mydata$predvalue, mydata$low)
auc <- performance(pred,"auc")
auc #auc即是C-statistics

#library(Hmisc)
somers2(mydata$predvalue, mydata$low) #somers2 {Hmisc}

五、logistic回归模型：亚组分析森林图绘制

化疗药物的反应率

Response	No.of patients	OR(95% CI)
Overall	1472	1.66(1.28,2.15)	1.66	1.28	2.15
Clinical stage
Advanced	951	1.67(1.23,2.26)	1.67	1.23	2.26
non-advanced	521	1.67(1.05,2.66)	1.67	1.05	2.66
ctDNA assays
qPCR	1280	1.73(1.30,2.29)	1.73	1.3	2.29
ARMS	192	1.58(0.50,5.04)	1.58	0.5	5.04
Ethnicity
Asian	326	1.93(0.84,4.43)	1.93	0.84	4.43
Caucasian	1146	1.57(1.20,2.06)	1.57	1.2	2.06

library(forestplot)
rs_forest <- read.csv('rs_forest.csv',header = FALSE)
# 读入数据的时候大家一定要把header设置成FALSE，保证第一行不被当作列名称。
# tiff('Figure 1.tiff',height = 1600,width = 2400,res= 300)
forestplot(labeltext = as.matrix(rs_forest[,1:3]),
           #设置用于文本展示的列，此处我们用数据的前三列作为文本，在图中展示
           mean = rs_forest$V4, #设置均值
           lower = rs_forest$V5, #设置均值的lowlimits限
           upper = rs_forest$V6, #设置均值的uplimits限
           is.summary = c(T,T,T,F,F,T,F,F,T,F,F),
           #该参数接受一个逻辑向量，用于定义数据中的每一行是否是汇总值，若是，则在对应位置设置为TRUE，若否，则设置为FALSE；设置为TRUE的行则以粗体出现
           zero = 1, #设置参照值，此处我们展示的是OR值，故参照值是1，而不是0
           boxsize = 0.4, #设置点估计的方形大小
           lineheight = unit(10,'mm'),#设置图形中的行距
           colgap = unit(3,'mm'),#设置图形中的列间距
           lwd.zero = 2,#设置参考线的粗细
           lwd.ci = 1.5,#设置区间估计线的粗细
           col=fpColors(box='#458B00', summary= "#8B008B",lines = 'black',zero = '#7AC5CD'),
           #使用fpColors()函数定义图形元素的颜色，从左至右分别对应点估计方形，汇总值，区间估计线，参考线
           xlab="The estimates",#设置x轴标签
           graph.pos = 3)#设置森林图的位置，此处设置为3，则出现在第三列

六、泊松回归模型

为阐述泊松回归模型的拟合过程，并探讨一些可能出现的问题，我们使用robust程辑包中的Breslow癫痫数据集（Breslow, 1993）。特别地，我们将讨论在治疗初期的8周内，抗癫痫药物对癫痫发病数的影响。请提前安装robust包。

我们就遭受轻微或严重间歇性癫痫的病人的年龄和癫痫发病数收集了数据，包含病人被随机分配到药物组或者安剂组前8周和随机分配后8周两种情况。响应变量为sumY（随机化后8周内癫痫发病数），预测变量为治疗条件（Trt）、年龄（Age）和前8周内的基础癫痫发病数。

# look at dataset
data(breslow.dat, package="robust")
names(breslow.dat)
summary(breslow.dat[c(6, 7, 8, 10)])

# plot distribution of post-treatment seizure counts
opar <- par(no.readonly=TRUE)
par(mfrow=c(1, 2))
attach(breslow.dat)
hist(sumY, breaks=20, xlab="Seizure Count", 
     main="Distribution of Seizures")
boxplot(sumY ~ Trt, xlab="Treatment", main="Group Comparisons")
par(opar)

# fit regression
fit <- glm(sumY ~ Base + Age + Trt, data=breslow.dat, family=poisson())
summary(fit)

# interpret model parameters
coef(fit)
exp(coef(fit))

# evaluate overdispersion
deviance(fit)/df.residual(fit)
library(qcc)
qcc.overdispersion.test(breslow.dat$sumY, type="poisson")

# fit model with quasipoisson
fit.od <- glm(sumY ~ Base + Age + Trt, data=breslow.dat,
              family=quasipoisson())
summary(fit.od)

结果解释：

在泊松回归中，年龄的回归参数为0.0227，表明保持其他预测变量不变，年龄增加1岁，癫痫发病数的对数均值将相应增加0.03。截距项即当预测变量都为0时，癫痫发病数的对数均值。由于不可能为0岁，且调查对象的基础癫痫发病数均不为0，因此本例中截距项没有意义。通常在因变量的初始尺度（癫痫发病数而非发病数的对数）上解释回归系数比较容易。为此，需要指数化回归系数。

指数化后，保持其他变量不变，年龄增加1岁，期望的癫痫发病数将乘以1.023。这意味着年龄的增加与较高的癫痫发病数相关联。更为重要的是， 1单位Trt的变化（即从安慰剂到治疗组），期望的癫痫发病数将乘以0.86，也就是说，保持基础癫痫发病数和年龄不变，服药组相对于安慰剂组癫痫发病数降低了20%。