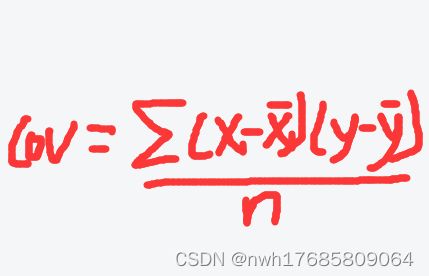学习ARIMA模型的心得

       对于初学者来说，了解第一个模型肯定是大概了解一下他内部的基本算法，不需要太懂，但得知道一些。首先，能看到这篇文章，大家肯定对ARIMA有一些基本的了解，他是由AR和MA模型综合而来的。

       那么，简要介绍这两个模型吧。开始我们必须得知道自相关系数和偏相关系数了，这两个是啥呢？大家可以从搜到一些计算的原理。我也简单的说一下。那么一开始呢我们有一组数据，比如就是【1，2，3，4，5】，通常来说我们学习相关系数一般是2组数据求解得来的，所以一组数据是没有相关系数的，但是自相关系数顾名思义，和自己相关，怎么弄呢。(但是重要的一点，我们后面计算的平均值方差都是整体数据得来的)。我们只需要把里面的数据拆解成2部分就行了，比如第一组【1，2，3，4】和第二组【2，3，4，5】，这个是一阶，二阶的两组数据是【1，2，3】和【3，4，5】有没有发现一些规律呢，一阶就是整体数据减掉一项，2阶就是减去两项。我们可以直接用excel计算并且和python的acf值对比，看是否准确。

自相关系数        

       从图可以看出我们的自相关系数需要计算出两组数据的协方差cov，然后除以两组数据的方差乘机开方，但是，上面我说过，平均值以及方差是基于整体数据的。

 

       计算数据【1，2，3，4】和【2，3，4，5】的cov时，我们减去的均值都是3，即整体的均值。数字10计算的是整体数据减去均值的平方和，如果除以n就是方差了，但是我们不需要，可以和上面的cov下面的分母约分掉。到这里便计算出一阶自相关，重复步骤，即可计算出各阶值。

      我们用python计算acf值

import numpy as np
from statsmodels.tsa.api import acf
data = np.array([1,2,3,4,5])
print(acf(data))

 结果和我们一致，只不过，在最前面加上了0阶的自相关系数，那就是1了。

偏相关系数的计算相对就比较麻烦了，需要用到Yule公式，我也不太会，这里面涉及到先求解协方差，然后求出协方差的对角矩阵，最后进行矩阵方差求解，代码如下

import numpy as np

a = np.array([1,2,3,4,5])
n = len(a)
a = a - np.mean(a)
order = 4
adj_needed = 1
r = np.zeros(order+1, np.float64)
r[0] = (a ** 2).sum() / n          #先求出第一个本身的 协方差  实际就是自己的方差
for k in range(1, order+1):
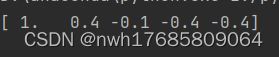
    r[k] = (a[0:-k] * a[k:]).sum() / (n - k * adj_needed)          #不能直接用公式求协方差  是因为 用的是整体的 均值，而不是独立出来样本的均值
print(r)
R = toeplitz(r[:-1])             #得到 对角矩阵
print(R)
rho = np.linalg.solve(R, r[1:])      #解方程组
print(rho, rho[-1])

理解了上面2部分，对于理解ARIMA方差便可以有一个大概的认识了，就是由几组数据通过复杂的计算，加上常数项和误差项。

 就是根据acf，pacf得到最佳阶数后（拖尾和截尾的问题），对上面的公式进行拟合，当然ARIMA和上面的区别就在于数据做差分，使其更平稳，通常就是用ADF检验，至于这个就不深入。大部分数据都可以一阶差分后得到平稳数据。

最后就是我们需要的ARIMA训练以及预测了。

但是我们不想去观看什么pacf图去确定p，q以及差分d的值，可以直接使用代码去代替我们得到最佳的答案。

min_bic = np.inf
best_order = None
best_arma = None
max_lag = 4
for p in range(max_lag):
    for d in range(max_lag):
        for q in range(max_lag):
            try:
                tmp_arma = tsa.ARIMA(train_data,order=(p,d,q)).fit()      
                tmp_bic = tmp_arma.bic
                if tmp_bic < min_bic:
                    min_bic = tmp_bic      #使用BIC 最小值进行取值
                    best_order = (p,d,q)
                    best_arma = tmp_arma
            except:
                continue

直接让他自行搜索到最优组合，即bic（贝叶斯信息量）值最小，这个可以简单理解我们得到的方程组拟合效果最好。

可以自行打印最优的参数组合best_order，但是我不建议用这种方法，太慢了，因为3个循环范围都是4，就会有64种结果，如果max_lag再大，会更慢。

可以采用自行查看一阶差分是否平稳，直接传入d的值可以有效缩短时间，完整的情况如下

data = data.close
train_data=data[:-30]  #划分好训练 和预测的数据集
test_data=data[-30:]
data_diff = data.diff().dropna()
adf = adfuller(data_diff)       #一般看第二个值是否小于0.05，如果是，便认为是平稳数据,如果这里一阶可以，下面的d值可以直接输入为1
print(adf[1]<0.05)   #为true说明一阶差分符合条件
min_bic = np.inf
best_order = None
best_arma = None
max_lag = 4
for p in range(max_lag):
    for q in range(max_lag):
        try:
            tmp_arma = tsa.ARIMA(train_data,order=(p,1,q)).fit()       #这里训练，不需要使用差分后的数据，否则还需要还原
            tmp_bic = tmp_arma.bic
            if tmp_bic < min_bic:
                min_bic = tmp_bic      #使用BIC 最小值进行取值
                best_order = (p,1,q)
                best_arma = tmp_arma
        except:
            continue
print(best_order)
# tmp_arma = tsa.ARIMA(train_data,order=(4,1,2)).fit()
# res = tmp_arma.forecast(30)
res = best_arma.forecast(30)
print(res)
predicted = res

index = test_data.index
predicted_data=pd.DataFrame(predicted,index=index)
fig = plt.figure()
plt.plot(data[-30:],c='blue')
plt.plot(predicted_data,c='red')
plt.legend(['ture','prediction'])
plt.show()

还有我们可以直接使用其他方法，除了上面的方法还可以使用其他方法查找最优参数，比如

auto_arima，网上有很多人讲解使用，这里不再叙述。