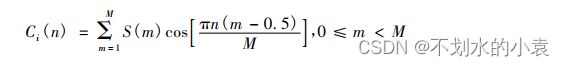MFCC声纹特征提取

目录

前言

预处理

特征参数提取

预加重

分帧

加窗

傅里叶变换

梅尔滤波器

离散余弦变换

结果展示

---

前言

语音识别本质上是一种模式识别的过程，其基本结构原理图如下图所示，主要包括语音信号预处理，特征参数提取，特征建模、模式匹配等几个功能模块。

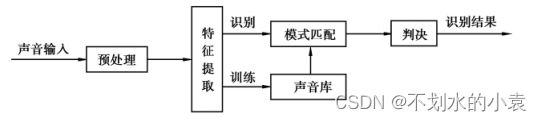一个声音识别系统主要包括训练和识别两个阶段，无论是训练还是识别，都需要对输入信号的原始声音进行预处理，并进行特征提取。在提取了相关的特征之后，识别的工作会变得相对简单很多，本文主要介绍声纹如何提取的。

预处理

声音信号的预处理包括滤波、A/D转换、预加重、分帧、端点检测等，假设经A/D转换后的数字音频信号为，预处理过程如下：

1) 归一化处理。归一化处理的目的是消除不同样本声音之间的大小差异，将样本幅值限定在范围内。

2）预加重。预加重通常使用带有6dB/倍频的一阶数字滤波器来实现，如：

其中为常数，通常取0.97。

3）对音频信号进行加窗分帧。虽然声音信号是非线性时变信号，但它具有短时平稳的特点，对其进行分帧可以提取其短时特性。通常取帧长为10~30ms，为了避免帧与帧之间的特性变化过大， 帧移通常取帧长的 1 /2， 即相邻帧之间有 1 /2 的重叠数据。为了进行短时分析， 必须通过加窗来选取窗口内的声音信号， 窗口外的声音信号为 0， 最常用的窗口函数是汉明窗。一般取 256 点为一帧， 帧间重叠为 128 点。

特征参数提取

        声音特征的选择取决于具体的系统， 比较有代表性的特征包括幅度( 或功率) 、过零率、线性预测系数特征矢量( LPC) 、LPC 倒谱特征矢量( LPCC) 、梅尔倒谱系数( MFCC) 等。特征提取完成对声音信号进行分析处理， 去掉与声音识别无关的冗余信息， 获得影响声音识别的重要信息。由于倒频谱( cepstrum) 有着能将频谱上的高低频分开的优点， 因此被广泛地应用在声音识别领域， 如 LPCC 和 MFCC。
 

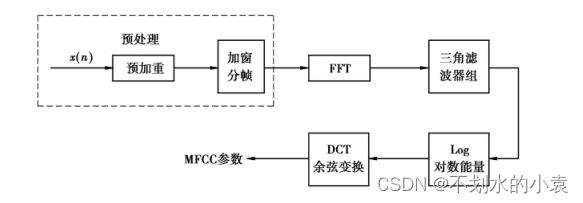         由于声音信号在时域上的变化快速且不稳定， 通常将它转换到频域上来分析其特征参数。梅尔倒频谱特征参数提取过程如上图所示。预处理后的声音数据经过快速傅里叶变换( FFT) ， 计算出每帧数据的频谱参数， 再将每帧数据的频谱参数通过一组 N( N 的值通常为 20 ～ 40) 个三角形带通滤波器构成的梅尔频率滤波器做卷积运算， 之后对每个频带的输出取对数， 求出每个输出的对数能量( Log Energy) S( m) ， m = 1， 2， 3， …， N。最后对此 N 个参数进行离散余弦变换， 求出梅尔倒谱系数作为声音特征参数

其中， n 为所取 MFCC 个数; Ci( n) 为第 i 帧的第 n 个 MFCC 系数; S( m) 为音频信号的对数功率谱; M 为三角滤波器个数。

预加重

        为了避免在后边的FFT操作中出现数值问题，我们需要加强一下高频信息，因为一般高频能量比低频小。其预加重函数如下所示：

        y(n)=x(n)−α⋅x(n−1)

分帧

        我们要对语音数据做傅里叶变换，将信息从时域转化为频域。但是如果对整段语音做FFT，就会损失时序信息。因此，我们假设在很短的一段时间t内的频率信息不变，对长度为t的帧做傅里叶变换，就能得到对语音数据的频域和时域信息的适当表达。举个例子，假如我们这里的采样点数为200000个点，如果真的这样做的话，就很麻烦了，于是我们在语音分析中引入分帧的概念，将原始语音信号分成大小固定的N段语音信号，这里每一段语音信号都被称为一帧。

加窗

        将信号分帧后,我们将每一帧代入窗函数，窗外的值设定为0，其目的是消除各个帧两端可能会造成的信号不连续性（即谱泄露 spectral leakage）。常用的窗函数有方窗、汉明窗和汉宁窗等，根据窗函数的频域特性，常采用汉明窗（hamming window）。接下来我来讲解一下怎么加窗：我们需要做的就是为每一帧数据，也就是301帧数据都加入大小为1103的汉明窗。其汉明窗的表达公式如下所示：

W(n)=(1−a)−a⋅cos(2⋅π⋅n/N)1≤n≤N

傅里叶变换

        傅里叶变换作为一个经常使用的东西，大家可以自行去了解，此处不过多赘述。

梅尔滤波器

        首先我要讲一下什么是梅尔值，这是一个新的量度，相比于正常的频率机制，梅尔值更加接近于人耳的听觉机制，其在低频范围内增长速度很快，但在高频范围内，梅尔值的增长速度很慢。每一个频率值都对应着一个梅尔值，其对应关系如下：

m=2595⋅log10​(1+f/700)

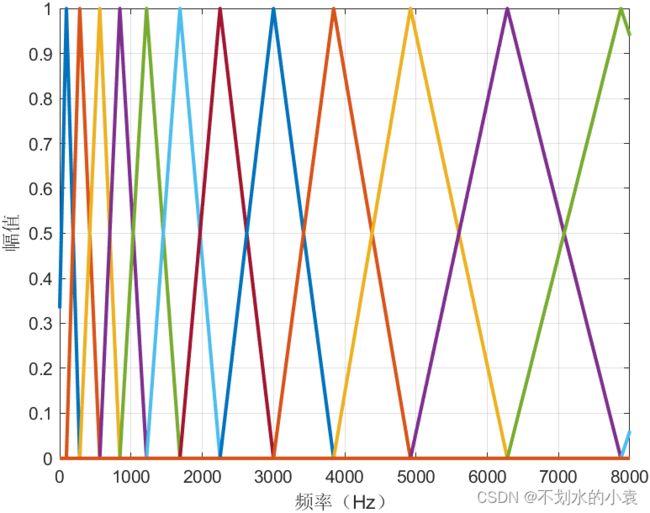如图展示了梅尔滤波器的一种形状，等高形式。

离散余弦变换

         在进行离散余弦变换之前，我们还需要做的就是把得到的二维矩阵能量谱 E，乘以得到的二维数组梅尔滤波器Hm的转置，得到参数H,其定义如下：

根据mfcc的定义，我们需要对能量的对数作离散余弦变换，即可得到MFCC参数：

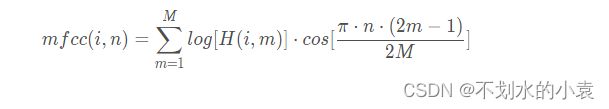 至此，声纹特征的提取过程到这里就结束了，特征提取出来之后，要对其进行识别就显得十分简单，GMM、SVM、BP等算法都可对其进行训练识别，并达到一个不错的效果。

结果展示

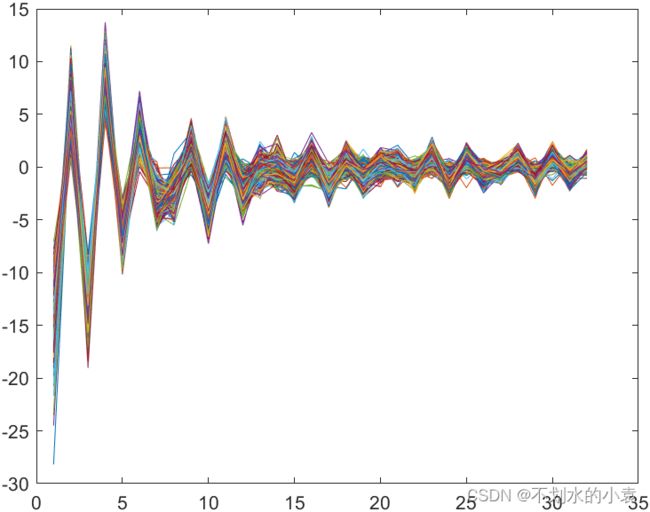
提取出来的特征如下图所示，变得有规律可循.

感谢观看，希望本文能对你有所帮助！