Time-Evolving Graph Convolutional Recurrent Network for Traffic Prediction论文笔记

Time-Evolving Graph Convolutional Recurrent Network for Traffic Prediction

总结

 本文提出了一种基于时间演化图卷积递归网络的流量预测模型。该方法采用张量分解方法生成自适应时间演化图（随时间变化的动态邻接矩阵），然后将这些时间演化图的图卷积模块集成到RNN结构中。在两个真实的交通数据集上的实验表明，TEGCRN比多个竞争基线模型更有优势，尤其是在短期预测方面。

挑战

1、交通状态的不确定性，在时域中存在复杂的非线性模式。一个节点（路段）的交通状况在不同的时间可能有相似的周期趋势，但在短时间内可能出现异常波动。如下图。交通速度表现出周期性，但在红色虚线框所示的短时间内可能会出现异常波动。

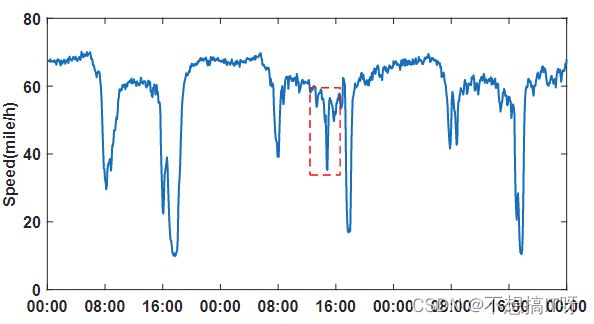
2、复杂的空间相关性。一个节点不仅与邻近的节点之间具有相似性，距离较远的两个节点也可能呈现出相似性的特点。如下图一天中三个相邻交通节点的交通速度，这三个节点的值表现出很强的相关性。

创新

&emsp之前研究在捕获空间相关性时，大多使用的是静态的邻接矩阵，但是节点之间的空间相关性动态变化的。本文提出了一种通用的流量预测框架——时间进化图卷积递归网络(TEGCRN)，该框架利用时间进化图卷积，在不同时隙自适应捕捉节点间动态依赖关系。贡献可以总结如下:

 1、基于张量分解的方法，利用自适应时间嵌入和节点嵌入构造了不同时间步的时间演进邻接图（邻接矩阵）。该方法充分利用了在时域中共享的信息，与每次慢速定义自适应图相比，参数效率更高（基于张量分解的方法可以减少参数量，消除冗余的参数）。
 2、为了对交通网络中的节点间模式进行建模，我们采用了一种混合跳图卷积，它利用了自适应时间演化图和预定义的基于距离的图。与静态图卷积模块相比，这种图卷积模块可以有效地捕获更全面的节点间依赖。
 3、将前述的图卷积模块与RNN编码器-解码器结构相结合，形成一个通用的交通预测框架，使其在建模交通序列特征时能够学习节点间依赖的动态。在两个真实的交通数据集上的实验表明，该模型优于多个竞争基线，特别是在短期预测方面。

Method

Method Overview

 下图说明了时间演进图卷积递归网络(TEGCRN)的概述。该模型主要由三部分组成。首先，利用自适应嵌入交通节点和时隙的张量组合方法生成时间演进的邻接图（图中红框部分）。然后，将得到的自适应图与预定义的静态基于距离的图$A^S$相结合，在图卷积模块中获取节点间信息。最后利用带时间演化图的图卷积模块取代GRU中的全连通层(就是将GRU单元中的线性层替换为图卷积），最后整个预测框架是编码器-解码器模型。在编码器-解码器的每个时间步中，根据一天中的时间选择不同的自适应图。该方法的核心思想是学习空间邻接的隐式动态和交通序列特征，从而获取更详细的时空信息。

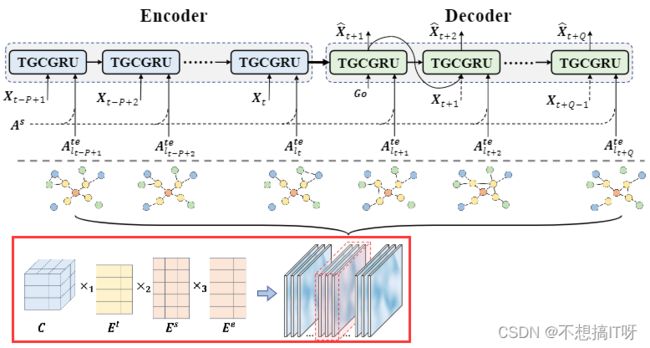
Generation of Time-Evolving Adaptive Graphs

 假定空间邻接的动态性遵循一天内的周期性，也就是不同天的相同时间段可以共享一个邻接图。将一天中每个时间步都对应单独的邻接矩阵（假设每隔5mins取一次数据，一天中的有288个时间步，这种方法可能会导致可训练参数数量较多，难以收敛，尤其是当交通节点N数量较大时。为了减少模型参数的数量，采用类似的张量分解的方法生成邻接图。本文使用的是基于 Tucker分解的张量分解方法。
 具体的构造方法为：
 将一天划分为$N_t$个时间步，道路网络中包含$N$个节点。首先构造三个嵌入矩阵${\mathbf{E}}^{\mathrm{t}}\in {\mathbb{R}}^{N_t\times d}$, ${\mathbf{E}}^{\mathbf{s}}\in {\mathbb{R}}^{N\times d}$,${\mathbf{E}}^{\mathbf{e}}\in {\mathbb{R}}^{N\times d}$和一个核心张量$C\in {\mathbb{R}}^{d\times d\times d}$，其中$d$为嵌入维数，$d\ll N$，三个嵌入矩阵分别表示时间节点嵌入、源节点嵌入、目标节点嵌入。核心张量$C$在这些嵌入之间建立联系，并对跨时间和空间共享的隐式因素建模。所有这些嵌入和核心张量都是可训练和随机初始化的。计算时空张量${\mathbf{A}}^{\prime }\in {\mathbb{R}}^{N_t\times N\times N}$的公式如下:$${\mathbf{A}}^{\prime }=\mathbf{C}\times {}_1{\mathrm{E}}^{\mathrm{t}}\times {}_2{\mathrm{E}}^{\mathrm{s}}\times {}_3{\mathrm{E}}^{\mathrm{e}}$$
${\mathrm{A}}^{\prime }$中的每个元素为：$${\mathbf{A}}_{i,j,k}^{\prime }=\sum _{w=1}^d\sum _{v=1}^d\sum _{u=1}^d{\mathbf{C}}_{u,v,w}{\mathbf{E}}_{i,u}^{\mathbf{t}}{\mathbf{E}}_{j,v}^{\mathbf{s}}{\mathbf{E}}_{k,w}^{\mathbf{e}}$$
然后对${\mathrm{A}}^{\prime }$进行归一化得到随时间变化的动态邻接图${\mathbf{A}}^{\text{te }}\in {\mathbb{R}}^{N_t\times N\times N}$：
$${\mathbf{A}}^{\text{te }}=\mathrm{softmax}\left(\mathrm{LeakyReLU}\left({\mathbf{A}}^{\prime }\right)\right)$$

 通过张量分解的方法生成动态邻接图（时间演化图），表示一天中不同时间步节点之间不同的相关性。之后，之后将用于图卷积模块中提取详细的空间信息。

Graph Convolution Module

 在使用图卷积捕获空间相关性时，同时使用的张量计算生成的动态邻接图和静态的邻接图。作者认为静态图捕获了局部模式，而从动态邻接图全局角度提供了动态节点间依赖关系。静态邻接图$A_s$的生成公式如下：
$${\mathbf{A}}_{i,j}^{\mathbf{s}}=\{\begin{array}{ll}\exp \left(-\frac{d_{v_i,v_j}^2}{{\sigma }^2}\right),& d_{v_i,v_j}\le \kappa \\ 0,& \text{ others }\end{array}$$
 考虑到深层网络的图卷积过平滑问题，作者将图卷积运算分为两个步骤:
 1、信息传播和加权mix-hop运算，类似于[21]中的方法。首先，对于某种类型的邻接图，根据图拓扑传播节点信息，生成$K$跳的节点表示。原点节点特征表示为${\mathbf{H}}_{\mathrm{in}}\in {\mathbb{R}}^{N\times d_{in}}$，经过$k-th$计算${\mathbf{H}}^{(k)}$表示为:$${\mathbf{H}}^{(k)}=(1-\alpha )\mathbf{A}{\mathbf{H}}^{(k-1)}+\alpha {\mathbf{H}}_{\mathbf{in}}$$

 本文也采用和了扩散卷积的思想：

Temporal Recurrent Module

 在每个时间步中，根据一天中的时间步选择不同的自适应图。然后将GRU中的线性层替换为图卷积模块。

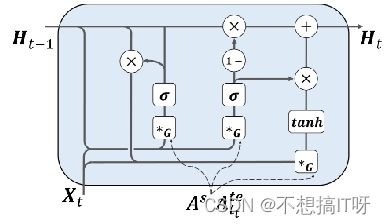
Experiments

使用的数据集是METR-LA PEMS-BAY,数据集描述如下：

预测结果：
METR-LA

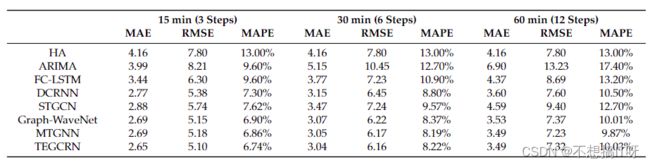
PEMS-BAY

消融实验

 作者对METR-LA数据集进行消融实验研究，以验证具有自适应时间演化图的图卷积模块的有效性。
 首先将TEGCRN中的时间演进图替换为中的静态自适应图。然后，进一步删除了时间演进的图生成模块，只使用静态预定义的基于距离的图。计算所有输出时间步的平均度量。结果如下表。可以看到，通过学习全局依赖，与自适应图的卷积比仅预定义的基于距离的图的卷积性能更高。

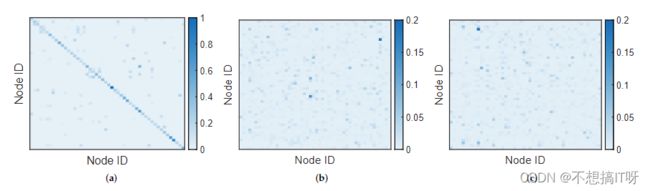
 此外，在TEGCRN中提出的时间进化图卷积通过捕捉更多隐式的节点间动态，进一步提高了预测性能。下图显示了归一化的基于距离的静态邻接图和学习的时间演进邻接图在某些选定的时隙中的热力图。颜色越深，对应节点之间的权重值越高。

&emsp论文的主要思想就是为每个时间步分配单独的邻接矩阵来捕获的动态的时间相关性，考虑到参数量过大的问题结合张量分解的方法以减少冗余的参数。和《Dynamic and Multi-faceted Spatio-temporal Deep Learning for Traffic Speed Forecasting》中的构造动态图的方法很相近。