图像分类中的基础概念+分类任务中常见损失函数介绍
一、图像分类中的基础概念
（一）、正负样本
- 标签为正样本，分类结果为正样本——True Positive（TP）——正确的正样本
- 标签为正样本，分类结果为负样本——False Negative（FN）——错误的负样本
- 标签为负样本，分类结果为正样本——False Positive（FP）——错误的正样本
- 标签为负样本，分类结果为负样本——True Negative（TN）——正确的负样本
| 真实值 预测值 | 正样本 | 负样本 |
|---|---|---|
| 正样本 | TP | FN |
| 负样本 | FP | TN |
（二）、精度、召回率、F1-score
1. 精度 (precision, 查准率) ：被判定为正样本的测试样本中，真正的正样本所占的比例
2. 召回率 (recall, 查全率) ：被判定为正样本的正样本占所有正样本的比例
3. F1-score：综合考虑了精度与召回率，其值越大则模型越好
精度与召回率的关系——相互矛盾的指标
- 召回率增加，精度下降
- 曲线与坐标值面积越大，性能越好
- 对正负样本不均衡问题敏感
图1 PR曲线
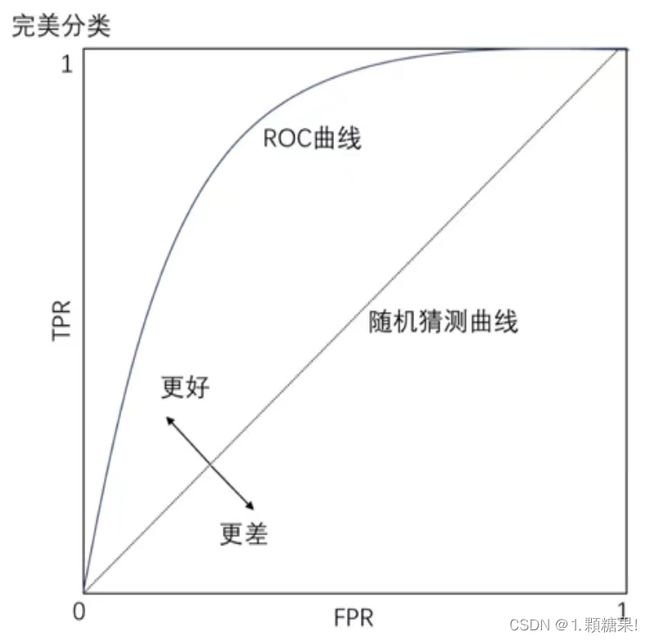
图2 ROC曲线（越偏向左上角越好）
ROC曲线解读：
横坐标：false positive rate(FPR)——正类中实际负实例占所有负实例的比例。
纵坐标：true positive rate(TPR)——正类中实际正实例占所有正实例的比例。
正负样本的分布变化，ROC曲线保持不变，对正负样本不均衡问题不敏感。
AUC：ROC曲线下的面积（ROC曲线以及右下角的面积），表示随机挑选一个正样本以及一个负样本，分类器会对正样本给出的预测值高于负样本的概率。
（三）、混淆矩阵——适用于多类别分类模型各个类别之间的分类情况
对于k分类问题，混淆矩阵为k*k矩阵，元素Cij表示第i类样本被分类器判定为第j类的数量。主对角线的元素之和为正确分类的样本数，其他元素之和为错误分类的样本数。对角线的值越大，分类器准确率越高。
混淆矩阵能很清晰的反映出各类别之间的错分概率，越好的分类器对角线上的值更大。
混淆矩阵的计算：
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1] # 正确的真值
y_pred = [0, 0 ,2, 2, 0, 2] # 分类器返回的估计目标
confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])二、分类任务优化目标——常见损失函数介绍
1. 0-1损失
只看分类的对与错，当标签与预测类别相等时，loss为0，否则为1
真实的优化目标，但是无法求导和优化，只有理论意义
2. 交叉熵损失
在介绍交叉熵的概念之前，我们先来回顾一下熵的概念：熵表示热力学系统的无序程度，在信息学中用于表示信息多少，不确定性越大，概率越低，则信息越多，熵越高。
熵是概率的单调递减函数：
交叉熵损失：表示第i个样本属于第j类的标签，表示第i个样本被预测为第j类的概率
参数说明：
- n——batchsize
- C——类别数
- ——第i个样本在第j类上的真实标签
- ——第i类样本在第j类上的预测概率
假设我们只有一个样本，两种类别，即
，，且有：
依旧假设我们只有1个样本，但是类别数为C，该样本的真实标签是属于第m类，则有
表示第i个样本所属的类别，表示第i个样本在其所属类别上的预测概率。
那么，将只包含一个样本的交叉熵损失公式推广到一个批次包含n个时，交叉熵损失就是n个样本各自交叉熵损失的求和平均，所以有
3. softmax loss及其变种
softmax loss是交叉熵损失的特例：神经网络中最后一层全连接层的输出结果成为logit，其范围为
，softmax的作用是将logit的范围转换到0~1，此时，第i个样本对第j类的预测概率就可以表示为：
其中，表示神经网络对第i个样本在第j类输出的logit。
所以，softmax loss的公式为：
交叉熵损失的变种：L softmaxloss
从内积的角度来理解最后一层全连接层的输出， ，即将分类的过程看作计算第i个样本
与神经网络最后一层全连接层权重
的余弦相似性，与最相似的
（内积最大）便对应着的类别。
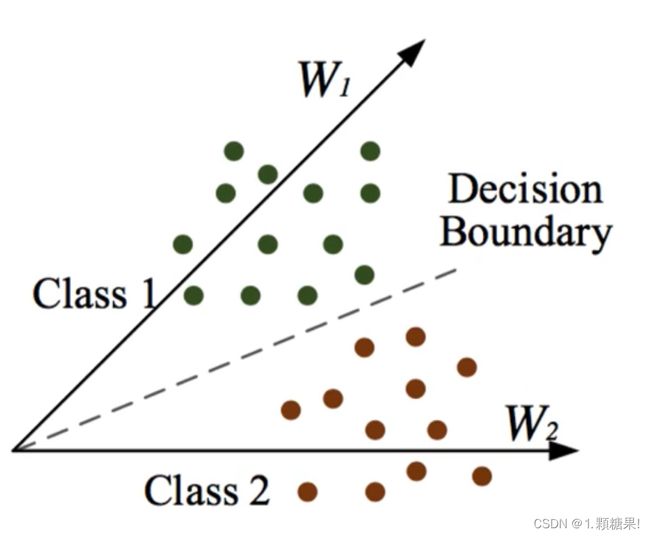
先考虑简单的二分类问题，即
图3 L_softmax_loss
若，样本就被分类为类别1；若，样本就被分类为类别2，所以分类的决策边界就是，我们考虑比较简单的情况，当是，决策边界就简化为。
那么我们如何使类内更加紧凑，类间更加分离呢？
首先，第i个样本被归为第一类，有，如果取预设常数m来确定样本接近真实类别的强度，使得，，结合余弦函数在[0,Π]的单调递减性质可知，
可推得比更小，从而实现了类内压缩并且类间更加疏离的效果。
图4 L_softmax_loss类内压缩类间分离
4. KL散度
KL散度用来估计两个分布p和q的相似性，其中分布p是数据的真实分布，我们用分布q来近似p。KL散度的作用就是计算用q分布近似p分布时损失了多少信息。
如果p是一个已知的分布（标签），则是一个常数，此时与交叉熵只有一个常数的差异。
KL散度的特性，大于等于0，当且仅当两个分布完全相同时等于0
这里需要注意的是KL散度不是距离，因为KL散度不对称，即。