2019年第十六届中国研究生数学建模竞赛F题·一种快速找到最优解的算法(提供Matlab源码)
2019年第十六届中国研究生数学建模竞赛F题·一种快速找到最优解的算法(提供Matlab源码)
目录
- 0. 源码+数据
- 1. 问题介绍
- 2. 贪心寻找较优解
-
- 2.1 算法步骤
- 2.2 源码
-
- 2.2.1 主程序
- 2.2.2 子函数
- 2.2.3 输出
- 3. 精确枚举寻找最优解
-
- 3.1 算法步骤
- 3.2 源码
-
- 3.2.1 主程序
- 3.2.2 子函数
- 3.2.3 输出
0. 源码+数据
链接:https://pan.baidu.com/s/1Autyo3Q_iDJ5ka8oD8LEag
提取码:gaec
1. 问题介绍
复杂环境下航迹快速规划是智能飞行器控制的一个重要课题。由于系统结构限制,这类飞行器的定位系统无法对自身进行精准定位,一旦定位误差积累到一定程度可能导致任务失败。因此,在飞行过程中对定位误差进行校正是智能飞行器航迹规划中一项重要任务。本题目研究智能飞行器在系统定位精度限制下的航迹快速规划问题。
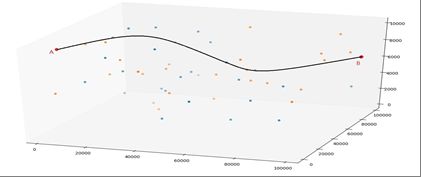
假设飞行器的飞行区域如下图所示,出发点为A点,目的地为B点。其航迹约束如下:
1)飞行器在空间飞行过程中需要实时定位,其定位误差包括垂直误差和水平误差。飞行器每飞行1m,垂直误差和水平误差将各增加δ个专用单位,,以下简称单位。到达终点时垂直误差和水平误差均应小于θ个单位,并且为简化问题,假设当垂直误差和水平误差均小于θ个单位时,飞行器仍能够按照规划路径飞行。
2)飞行器在飞行过程中需要对定位误差进行校正。飞行区域中存在一些安全位置(称之为校正点)可用于误差校正,当飞行器到达校正点即能够根据该位置的误差校正类型进行误差校正。校正垂直和水平误差的位置可根据地形在航迹规划前确定(如图1为某条航迹的示意图, 黄色的点为水平误差校正点,蓝色的点为垂直误差校正点,出发点为A点,目的地为B点,黑色曲线代表一条航迹)。可校正的飞行区域分布位置依赖于地形,无统一规律。若垂直误差、水平误差都能得到及时校正,则飞行器可以按照预定航线飞行,通过若干个校正点进行误差校正后最终到达目的地。
3)在出发地A点,飞行器的垂直和水平误差均为0。
4)飞行器在垂直误差校正点进行垂直误差校正后,其垂直误差将变为0,水平误差保持不变。
5)飞行器在水平误差校正点进行水平误差校正后,其水平误差将变为0,垂直误差保持不变。
6)当飞行器的垂直误差不大于α_1个单位,水平误差不大于α_2个单位时才能进行垂直误差校正。
7)当飞行器的垂直误差不大于β_1个单位,水平误差不大于β_2个单位时才能进行水平误差校正。
请你们团队为上述智能飞行器建立从A点飞到B点的航迹规划一般模型和算法并完成以下问题:
问题1. 针对附件1中的数据规划满足条件(1)~(7)时飞行器的航迹,并且综合考虑以下优化目标:
(A)航迹长度尽可能小;(B)经过校正区域进行校正的次数尽可能少。
其中附件1数据的参数为:
α 1 = 25 , α 2 = 15 , β 1 = 20 , β 2 = 25 , θ = 30 , δ = 0.001 {\alpha _1} = 25,{\alpha _2} = 15,{\beta _1} = 20,{\beta _2} = 25,\theta = 30,\delta = 0.001 α1=25,α2=15,β1=20,β2=25,θ=30,δ=0.001
2. 贪心寻找较优解
2.1 算法步骤
- 寻找可行驶到的下一步
- 评估下一步:到终点的距离小为优(飞行器行驶到下一校正点时,可能累计误差小于 θ 评估下一步:到终点的距离小为优(飞行器行驶到下一校正点时,可能累计误差小于\theta 评估下一步:到终点的距离小为优(飞行器行驶到下一校正点时,可能累计误差小于θ, )
- 以50条优解进行同时搜索
- 待达到终点后,选择路程最短的解为输出
2.2 源码
2.2.1 主程序
% 2019年第十六届中国研究生数学建模竞赛F题·多约束条件下智能飞行器航迹快速规划
% --优先考虑增添误差长度后到终点的距离
% 目录
% a. 预处理
% b. 主循环
% b.1 寻找下一步的可行点
% b.2 评价
% b.3 选择
% c. 可视化输出
% _________________________________________________________________________________________
%% a. 预处理
clear,clc
load data1.mat
% 第一列 校正点的序号
% 第二至四列 x,y,z坐标
% 第五列 校正点的类型(0表示水平误差校正点,1表示垂直误差校正点,2表示起点,3表示终点)
data1(:,1) = data1(:,1)+1; % 编号从0开始,更改为从1开始
a1 = 25;
a2 = 15;
b1 = 20;
b2 = 25;
c = 30;
d = 0.001;
Goal_Coordinate = data1(end,2:4); % 终点坐标
max_Length = c/0.001; % 正常行驶的最大距离
% 各点之间的代价矩阵
tic
Cost_matrix = zeros(size(data1,1),size(data1,1));
Length_matrix = zeros(size(data1,1),size(data1,1));
for i = 1:size(data1,1)
for j = 1:size(data1,1)
Length_matrix(i,j) = sqrt(sum((data1(i,2:4)-data1(j,2:4)).^2));
Cost_matrix(i,j) = Length_matrix(i,j);
if Length_matrix(i,j) >= max_Length
Cost_matrix(i,j) = inf;
else
Cost_matrix(i,j) = Cost_matrix(i,j)*d;
end
end
end
toc
%% b. 主循环
tic
New_path = [{1},{[0,0]},{inf},{0}];
while isempty(find(cell2mat(New_path(:,4))==1, 1))
Mother_New_path = {};
for j = 1:size(New_path,1)
%% b.1 寻找下一步的可行点
% 当前点信息
num = New_path{j,1}(end,1); % 当前点编号
Coordinate = data1(num,2:4); % 当前点的坐标
Vertical_error = New_path{j,2}(1,1); % 当前点的垂直误差
Horizontal_error = New_path{j,2}(1,2); % 当前点的水平误差
% 寻找下一步可行点
Path_Vertical = [];
Path_Horizontal = [];
for i = 2:size(data1,1)
if isempty(find(New_path{j,1}==i, 1)) && Cost_matrix(num,i) ~= inf % 如果和之前的路径不重复,并在最大距离以内
% 分以下三种情况:
% 可以走当前路径,并能够进行垂直校正,保存路径
% 可以走当前路径,并能够进行水平校正,保存路径
% 附:如果三种情况都不存在,既是没有可行的下一步节点
if (Cost_matrix(num,i)+Vertical_error <= a1) && (Cost_matrix(num,i)+Horizontal_error <= a2) && data1(i,5) == 1
Path_Vertical(end+1,:) = [i,0,Cost_matrix(num,i)+Horizontal_error];
elseif (Cost_matrix(num,i)+Vertical_error <= b1) && (Cost_matrix(num,i)+Horizontal_error <= b2) && data1(i,5) == 0
Path_Horizontal(end+1,:) = [i,Cost_matrix(num,i)+Vertical_error,0];
end
end
end
% 所有的待选择路径 Path_selecting
% 第一列是节点序号
% 第二列是垂直误差
% 第三列是水平误差
% 第四列是到终点的距离
Path_selecting = [Path_Vertical;Path_Horizontal];
if isempty(Path_selecting)
continue
end
for i = 1:size(Path_selecting,1)
Path_selecting(i,4) = Length_matrix(data1(end,1),data1(Path_selecting(i,1),1));
Path_selecting(i,5) = Length_matrix(data1(end,1),data1(Path_selecting(i,1),1))-max(Path_selecting(i,2:3))/d;
end
%% b.2 评价
Evaluate = sortrows(Path_selecting,5); % 按照终点的距离排序
%% b.3 选择
Path_choosed = Evaluate(1:ceil(0.8*size(Evaluate,1)),1:4);
Son_New_path = cell(size(Path_choosed,1),2);
for i = 1:size(Path_choosed,1)
Son_New_path(i,1) = {[New_path{j,1};Path_choosed(i,1)]}; % 第一列为当前路径(使用点的编号表示)
Son_New_path(i,2) = {Path_choosed(i,2:3)}; % 第二列为当前路径的垂直误差和水平误差
Son_New_path(i,3) = {Path_choosed(i,4)}; % 第三列为剩余距离
if ((c-max(Son_New_path{i,2}))/d)-Path_choosed(i,4) >=0
Son_New_path(i,4) = {1};
else
Son_New_path(i,4) = {0};
end
end
Mother_New_path(end+1:end+size(Son_New_path,1),:) = Son_New_path;
end
[~,index] = sort(cell2mat(Mother_New_path(:,3)));
if size(index,1)>100
New_path = Mother_New_path(index(1:50,:),:);
else
New_path = Mother_New_path(index(1:ceil(0.5*size(index,1))),:);
end
end
New_path = New_path(cell2mat(New_path(:,4))==1,1); % 提取所有的可行路径
for i = 1:size(New_path,1)
New_path{i,1}(end+1,1) = data1(end,1); % 加上终点
New_path{i,2} = size(New_path{i,1},1); % 统计点数
Length = 0;
for j = 1:size(New_path{i,1},1)-1
Length = Length+Length_matrix(New_path{i,1}(j+1,1),New_path{i,1}(j,1));
end
New_path{i,3} = Length; % 统计距离
end
[~,b] = sort(cell2mat(New_path(:,3)));
Result = New_path(b,:);
toc
%% c. 可视化输出
close all
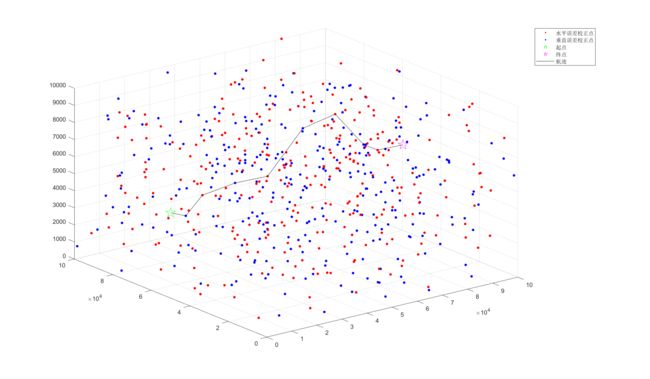
show(data1,Result{1, 1});
% 1.049
2.2.2 子函数
function show(data,path)
%% 散点图
H_correct = data(data(:,5)==0,:); % 水平误差校正点
V_correct = data(data(:,5)==1,:); % 垂直误差校正点
start_end = data([1,end],:); % 起点,终点坐标
figure(1)
scatter3(H_correct(:,2),H_correct(:,3),H_correct(:,4),200,'.','r') % H_correct
hold on
scatter3(V_correct(:,2),V_correct(:,3),V_correct(:,4),200,'.','b') % V_correct
scatter3(start_end(1,2),start_end(1,3),start_end(1,4),300,'p','g') % start point
scatter3(start_end(2,2),start_end(2,3),start_end(2,4),300,'p','m') % end point
%% 路线图
path1data = data(path,:);
for i = 2:size(path1data,1)
if i>1
plot3(path1data(i-1:i,2),path1data(i-1:i,3),path1data(i-1:i,4),'color','k');
end
pause(0.05);
end
legend('水平误差校正点','垂直误差校正点','起点','终点','航迹');
hold off
2.2.3 输出
- Path0 : [ 1 504 70 238 156 339 458 556 437 613 ] | 10次校正(包含起始点) | 路程长度:10489.84
3. 精确枚举寻找最优解
3.1 算法步骤
- 输入贪心算法得到的解
- 对所有的路径自起点开始逐步枚举
- 对路径进行精确删减(如果已经行驶的路程+当前位置到终点的距离>贪心算法得到路程长度,则进行删减)
- 保留所有寻找到的解,进行pareto排序,取第一前沿为输出
3.2 源码
3.2.1 主程序
% 2019年第十六届中国研究生数学建模竞赛F题
% 多约束条件下智能飞行器航迹快速规划
% -- 精确穷举
% 目录
% a. 预处理
% b. 主循环
% b.1 寻找下一步的可行点
% c. 可视化输出
%% a. 预处理
clear,clc
load data1.mat
% 第一列 校正点的序号
% 第二至四列 x,y,z坐标
% 第五列 校正点的类型(0表示水平误差校正点,1表示垂直误差校正点,2表示起点,3表示终点)
data1(:,1) = data1(:,1)+1; % 编号从0开始,更改为从1开始
% data1(100:500,:) = [];
% data1(:,1) = (1:size(data1,1));
a1 = 25;
a2 = 15;
b1 = 20;
b2 = 25;
c = 30;
d = 0.001;
max_length = pdist2(data1(1,2:4),data1(end,2:4));
max_error = 1.049*100000 - max_length;
vector_start_goal = (data1(end,2:4)-data1(1,2:4));
Goal_Coordinate = data1(end,2:4); % 终点坐标
max_Length = c/0.001; % 正常行驶的最大距离
% 各点之间的代价矩阵
tic
Cost_matrix = zeros(size(data1,1),size(data1,1));
Length_matrix = zeros(size(data1,1),size(data1,1));
for i = 1:size(data1,1)
for j = 1:size(data1,1)
Length_matrix(i,j) = sqrt(sum((data1(i,2:4)-data1(j,2:4)).^2));
Cost_matrix(i,j) = Length_matrix(i,j);
if Length_matrix(i,j) >= max_Length
Cost_matrix(i,j) = inf;
else
Cost_matrix(i,j) = Cost_matrix(i,j)*d;
end
end
end
toc
%% b. 主循环
tic
New_path = [{1},{[0,0]},{inf},{0}];
sss = cell(1,4);
while ~isempty(New_path)
Mother_New_path = {};
for j = 1:size(New_path,1)
%% b.1 寻找下一步的可行点
% 当前点信息
num = New_path{j,1}(end,1); % 当前点编号
Coordinate = data1(num,2:4); % 当前点的坐标
Vertical_error = New_path{j,2}(1,1); % 当前点的垂直误差
Horizontal_error = New_path{j,2}(1,2); % 当前点的水平误差
if size(New_path{j,1},1) > 1
Length = 0;
for ss = 1:size(New_path{j,1},1)-1
Length = Length+Length_matrix(New_path{j,1}(ss+1,1),New_path{j,1}(ss,1));
end
Length_AC = Length; % 统计距离
else
Length_AC = 0;
end
% 寻找下一步可行点
Path_Vertical = [];
Path_Horizontal = [];
for i = 2:size(data1,1)
if isempty(find(New_path{j,1}==i, 1)) && Cost_matrix(num,i) ~= inf % 如果和之前的路径不重复,并在最大距离以内
% 分以下三种情况:
% 可以走当前路径,并能够进行垂直校正,保存路径
% 可以走当前路径,并能够进行水平校正,保存路径
% 附:如果三种情况都不存在,既是没有可行的下一步节点
if (Cost_matrix(num,i)+Vertical_error <= a1) && (Cost_matrix(num,i)+Horizontal_error <= a2) && data1(i,5) == 1
Path_Vertical(end+1,:) = [i,0,Cost_matrix(num,i)+Horizontal_error];
elseif (Cost_matrix(num,i)+Vertical_error <= b1) && (Cost_matrix(num,i)+Horizontal_error <= b2) && data1(i,5) == 0
Path_Horizontal(end+1,:) = [i,Cost_matrix(num,i)+Vertical_error,0];
end
end
end
% 所有的待选择路径 Path_selecting
% 第一列是节点序号
% 第二列是垂直误差
% 第三列是水平误差
% 第四列是到终点的距离
Path_selecting = [Path_Vertical;Path_Horizontal];
if isempty(Path_selecting)
continue
end
for i = 1:size(Path_selecting,1)
Path_selecting(i,4) = Length_matrix(data1(end,1),data1(Path_selecting(i,1),1)); % 到终点的距离
Length_AC1 = Length_AC + Length_matrix(num,data1(Path_selecting(i,1),1));
Path_selecting(i,5) = Length_AC1 + Path_selecting(i,4) - max_length - max_error;
end
if isempty(find(Path_selecting(:,5)<=0, 1))
continue
else
Path_selecting(Path_selecting(:,5)>0,:) = [];
end
Path_choosed = Path_selecting(:,1:4);
Son_New_path = cell(size(Path_choosed,1),2);
for i = 1:size(Path_choosed,1)
Son_New_path(i,1) = {[New_path{j,1};Path_choosed(i,1)]}; % 第一列为当前路径(使用点的编号表示)
Son_New_path(i,2) = {Path_choosed(i,2:3)}; % 第二列为当前路径的垂直误差和水平误差
Son_New_path(i,3) = {Path_choosed(i,4)}; % 第三列为剩余距离
if ((c-max(Son_New_path{i,2}))/d)-Path_choosed(i,4) >=0
Son_New_path(i,4) = {1};
else
Son_New_path(i,4) = {0};
end
end
Mother_New_path(end+1:end+size(Son_New_path,1),:) = Son_New_path;
end
if ~isempty(Mother_New_path)
sss = [sss;Mother_New_path(cell2mat(Mother_New_path(:,4))==1,:)] ;
Mother_New_path(cell2mat(Mother_New_path(:,4))==1,:) = [];
New_path = Mother_New_path;
else
break
end
end
New_path = sss(2:end,:);
for i = 1:size(New_path,1)
New_path{i,1}(end+1,1) = data1(end,1); % 加上终点
New_path{i,2} = size(New_path{i,1},1); % 统计点数
Length = 0;
for j = 1:size(New_path{i,1},1)-1
Length = Length+Length_matrix(New_path{i,1}(j+1,1),New_path{i,1}(j,1));
end
New_path{i,3} = Length; % 统计距离
end
[~,b] = sort(cell2mat(New_path(:,3)));
Result = New_path(b,:);
toc
%% c. 可视化输出
close all
[sorted_based_on_front] = Pareto_front_rank([ cell2mat(Result(:,2)),cell2mat(Result(:,3))/10000],2);
for i = 1:size(sorted_based_on_front,1)
if sorted_based_on_front(i,3) == 1
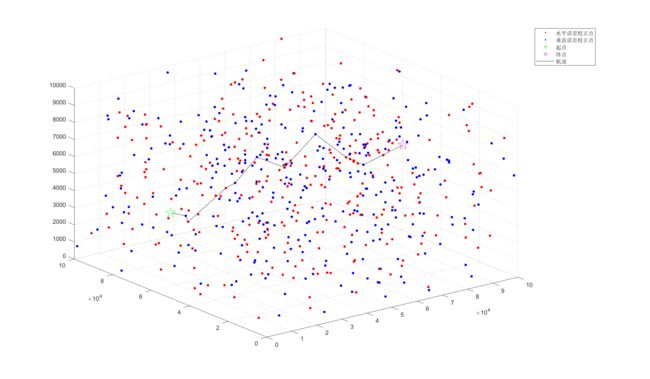
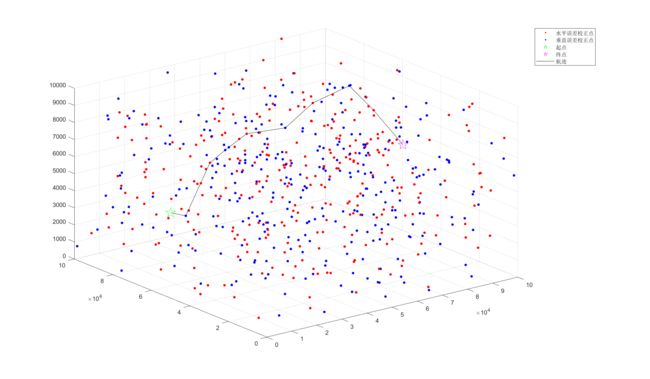
show(data1,Result{sorted_based_on_front(i,4), 1})
Result{sorted_based_on_front(i,4),1}
close all
else
break
end
end
3.2.2 子函数
function [sorted_based_on_front]=Pareto_front_rank(x,n_obj)
% Input x 需要pareto前沿排序的点集合,一行代表一个点,一列代表点的一个维
% n_obj 表示点坐标的维度,也即是目标的个数
% Output sorted_based_on_front 返回x的第n_obj+1列就是pareto前沿排序的序号
% sorted_based_on_front 倒数第二列是pareto前沿排序,倒数第一列是原索引
N=size(x,1);%计算要排序点的个数
front = 1;
F(front).f = [];
individual = [];
for i = 1 : N
% Number of individuals that dominate this individual
individual(i).n = 0;
% Individuals which this individual dominate
individual(i).p = [];
for j = 1 : N
dom_less = 0;
dom_equal = 0;
dom_more = 0;
for k = 1 : n_obj
if (x(i,k) < x(j,k))
dom_less = dom_less + 1;
elseif (x(i,k) == x(j,k))
dom_equal = dom_equal + 1;
else
dom_more = dom_more + 1;
end
end
if dom_less == 0 && dom_equal ~= n_obj
individual(i).n = individual(i).n + 1;
elseif dom_more == 0 && dom_equal ~= n_obj
individual(i).p = [individual(i).p j];
end
end
if individual(i).n == 0
x(i,n_obj + 1) = 1;
F(front).f = [F(front).f i];
end
end
% Find the subsequent fronts
while ~isempty(F(front).f)
Q = [];
for i = 1 : length(F(front).f)
if ~isempty(individual(F(front).f(i)).p)
for j = 1 : length(individual(F(front).f(i)).p)
individual(individual(F(front).f(i)).p(j)).n = ...
individual(individual(F(front).f(i)).p(j)).n - 1;
if individual(individual(F(front).f(i)).p(j)).n == 0
x(individual(F(front).f(i)).p(j),n_obj + 1) = ...
front + 1;
Q = [Q individual(F(front).f(i)).p(j)];
end
end
end
end
front = front + 1;
F(front).f = Q;
end
x(:,end+1)=(1:size(x,1))';
sorted_based_on_front=sortrows(x,n_obj+1);
% [temp,index_of_fronts] = sort(x(:,n_obj + 1));
% for i = 1 : length(index_of_fronts)
% sorted_based_on_front(i,:) = x(index_of_fronts(i),:);
% end
end