CV第一篇:EDLines基础理论
EDLines: A real-time line segment detector with a false detection control
简介
图像信息特征的描述大致分为角点特征、线特征和语义特征。点特征如harris、sfit、surf、orb等点特征,线特征主要包括如hough、houghP、Etemadi、LSD等等。
论文提出了一种超快的直线检测器EDLines,在保证实时性的同时抑制了误检量,并对比了以上特征在提取质量和速度上的差异,得出该检测器在保证较高准确性的同时,其速度比现有直线检测器的快至少一个数量级。
- 论文地址:
百度网盘 论文 提取码:a3eu
百度网盘 代码 提取码:8q5e
论文解读
EDLines的基本结构分为以下三部分:
- 输入灰度图,利用Edge Drawing算法进行提取,输出一系列连续的像素点
- 利用最小二乘法来连接像素点,避免连到外点
- 用Desolneux等提出的Helmholtz Principle来抑制误检的线段
1、Edge Drawing检测算法
ED检测算法大致分为以下4个步骤:
| 步骤 | 操作 | 作用/示例 |
|---|---|---|
| 1 | 滤波核遍历图像 | 高斯滤波,抑制噪声 |
| 2 | 计算像素梯度 | Prewitt,Sobel等算子 |
| 3 | 选出梯度较大者为“锚” | “锚”(anchors)极可能为线段 |
| 4 | 连接锚点 | 生成初始线段 |
演示如下图所示
2、线段提取
拟合好的线段事实上并不符合要求,因为初始线段连接了所有锚点,如上图(d)所示,线段是由每个相连的锚点拼接而成,并不光滑。
因此需要筛选掉没有价值的中间点,使线段更为平滑。这里使用的是最小二乘法。
最小二乘法( the Least Squares Line Fitting )
3、线段筛选
经过简单生成和提取的线段可能并不能选取合适的线段数量,如Hough直线检测由于缺乏筛选验证的部分因此可能导致过拟合或者欠拟合(实际上是中间参数选取不合理导致)
因此,需要中间参数进行合理估计和选择,才能得到适当数量和位置的拟合线段。
这里就需要用到前面提到的Helmholtz Principle来选取合适的线段
// 伪代码
LineFit(Pixel ⁄pixelChain, int noPixels){
double lineFitError = INFINITY; // current line fit error
LineEquation lineEquation; // y = ax + b OR x = ay + b
while (noPixels > MIN_LINE_LENGTH){
LeastSquaresLineFit(pixelChain, MIN_LINE_LENGTH, &lineEquation,
&lineFitError);
if (lineFitError <= 1.0) break; // OK. An initial line segment detected
pixelChain ++; // Skip the first pixel & try with the remaining pixels
noPixels–; // One less pixel
} // end-while
if (lineFitError > 1.0) return; // no initial line segment. Done.
// An initial line segment detected. Try to extend this line segment
int lineLen = MIN_LINE_LENGTH;
while (lineLen < noPixels){
double d = ComputePointDistance2Line(lineEquation,
pixelChain[lineLen]);
if (d > 1.0) break;
lineLen++;
} //end-while
// End of the current line segment. Compute the final line equation & output it.
LeastSquaresLineFit(pixelChain, lineLen, &lineEquation);
Output ‘‘lineEquation’’
// Extract line segments from the remaining pixels
LineFit(pixelChain + lineLen, noPixels-lineLen);
} //end-LineFit
//下一次讨论代码
此部分思想源于Desolneux提出的方法,主要思路是引入一个*NFA(Number of False Alarms,误检数量)*的概念
首先提出梯度值和梯度角的概念
3.1、计算像素的梯度
每个点的梯度值*m(x,y)*和梯度角 θ ( x , y ) \theta(x,y) θ(x,y)
一般的梯度和梯度角度公式:
m ( x , y ) = [ L ( x + 1 , y ) − L ( x − 1 , y ) ] 2 + L ( x , y + 1 ) − L ( x , y − 1 ) ] 2 m(x,y) = \sqrt{[L(x+1,y)-L(x-1,y)]^2+L(x,y+1)-L(x,y-1)]^2} m(x,y)=[L(x+1,y)−L(x−1,y)]2+L(x,y+1)−L(x,y−1)]2
θ ( x , y ) = a r c t a n L ( x , y + 1 ) − L ( x , y − 1 ) L ( x + 1 , y ) − L ( x − 1 , y ) \theta(x,y) = arctan{\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}} θ(x,y)=arctanL(x+1,y)−L(x−1,y)L(x,y+1)−L(x,y−1)
论文的梯度和梯度角度公式:
g x ( x , y ) = L ( x + 1 , y ) − L ( x , y ) + L ( x + 1 , y + 1 ) − L ( x , y + 1 ) 2 g_x(x,y) = \frac{L(x+1,y)-L(x,y)+L(x+1,y+1)-L(x,y+1)}{2} gx(x,y)=2L(x+1,y)−L(x,y)+L(x+1,y+1)−L(x,y+1)
g y ( x , y ) = L ( x , y + 1 ) − L ( x , y ) + L ( x + 1 , y + 1 ) − L ( x + 1 , y ) 2 g_y(x,y) = \frac{L(x,y+1)-L(x,y)+L(x+1,y+1)-L(x+1,y)}{2} gy(x,y)=2L(x,y+1)−L(x,y)+L(x+1,y+1)−L(x+1,y)
g ( x , y ) = [ g x ( x , y ) ] 2 + [ g y ( x , y ) ] 2 g(x,y) = \sqrt{[g_x(x,y)]^2+[g_y(x,y)]^2} g(x,y)=[gx(x,y)]2+[gy(x,y)]2θ ( x , y ) = a r c t a n g x ( x , y ) − g y ( x , y ) \theta(x,y) = arctan{\frac{g_x(x,y)}{-g_y(x,y)}} θ(x,y)=arctan−gy(x,y)gx(x,y)
每个特征点可以得到三个信息*(x,y,m, θ \theta θ),*即位置,尺度和方向。梯度值为非负数,而角度范围为360°
箭头的大小和方向为梯度大小*m(x,y)*和梯度角 θ ( x , y ) \theta(x,y) θ(x,y)
3.2 、NFA(误检线段数量)
定义一张尺寸为NxN个像素的图像,A为一段线段,其中n 为 A 的线段长度,像素值;k为 A 上与A方向一致的点的数目
N F A ( n , k ) = N 4 ⋅ ∑ i = k n ( n i ) p i ( 1 − p ) n − i NFA(n,k) = N^4 ·\sum_{i=k}^n \binom{n}{i} p^i (1-p)^ {n-i} NFA(n,k)=N4⋅i=k∑n(in)pi(1−p)n−i
其中 N 4 \N^4 N4 为NxN图像潜在线段的数量,因为图像有NxN个像素点,而两个点确定一个线段,共 N 2 N^2 N2个点,因此共有 N 4 N^4 N4条可能的线段
NFA代表一张图像的误检线段数量
论文设定NFA有意义的条件是NFA(n,k)<= ε \varepsilon ε,实际上一般取1,即一张图像允许一个误检线段
具体验证过程:
对于长度为n的线段,计算沿线段的每个像素的梯度角和与线段方向一致的像素点数量k,
然后计算NFA的值
若NFA<= 1,则线段有效;否则丢弃
事实上验证筛选是可选的,因为短线段会被筛选掉,而长线段会被保留
4、参数选取(对ED和NFA参数值的讨论)
线段的筛选实际上是基于线段长度和方向一致像素点的数量的。
- NFA中的p的选取
论文首先定义了方向一致这个概念:
梯度角度计算时的范围为360°,但判定方向时不需要如此细致的划分,就像SFIT特征,其直方图将360°划分为8份再进行方向统计,
类似的,此处也是一样的思路,将360°划分为8等份,即22.5°,方向一致定义为线段方向与像素梯度方向处于22.5°之内
因此公式1选取的p值为1/8 = 0.125
- Edge Drawing算法中的 ρ \rho ρ的选取
ρ \rho ρ是一个阈值常数,大于 ρ \rho ρ的梯度值才被计入统计,否则去掉,作用是在ED算法中筛选出是否认定为锚点的像素点。
锚点中两像素点的最大数值误差为2(一正一负),角度误差为22.5°。即数值误差小于2,方向误差小于22.5°才作为锚点,因此:
ρ = 2 s i n ( 22.5 ° ) = 5.22 \rho = \frac{2}{sin(22.5°)} = 5.22 ρ=sin(22.5°)2=5.22
遍历图像,小于 ρ \rho ρ值得到的点称为边缘区域
- Edge Drawing算法中的anchor threshold的选取
实际上就是NMS(non-maximal suspression,非最大抑制)。传统的NMS的依据是判断一个像素点的梯度是否大于周边像素的梯度值
而论文改进的NMS是判断一个像素点的梯度是否比周边像素的梯度值大anchor threshold个值
论文对anchor threshold的选择采用实验的方法,得到anchor threshold = 3较为理想
- Edge Drawing算法中的scan interval的选取
扫描间隔,即NFA公式中k的值,代表每隔多少圈扫描一次像素值。默认为1,保证像素全部扫描到。
重新把NFA公式列一下
N F A ( n , k ) = N 4 ⋅ ∑ i = k n ( n i ) p i ( 1 − p ) n − i NFA(n,k) = N^4 ·\sum_{i=k}^n \binom{n}{i} p^i (1-p)^ {n-i} NFA(n,k)=N4⋅i=k∑n(in)pi(1−p)n−i
且有NFA(n,k)<= ε \varepsilon ε,实际上一般 ε \varepsilon ε取1
-
线段拟合中的Minimum line length的选取
对于过短的线段(即首末像素的距离长度小于一定值),可以直接过滤掉
之前提到NFA(n,k)<= 1来保证像素和线段的方向一致。要使得最小线长有效,必有
k = n,得到 N F A ( n , n ) = N 4 ⋅ P 4 ≤ 1 NFA(n,n) = N^4·P^4 \leq 1 NFA(n,n)=N4⋅P4≤1移项可得 n ≤ − 4 l o g ( N ) l o g ( p ) n \leq \frac{-4log(N)}{log(p)} n≤log(p)−4log(N),其中p = 0.125。对于一个512x512的图像,最小线段长应为12像素
-
线段拟合中的maximum mean square line fit error的选取
最大平方根误差用于线段拟合,当误差大于一定值,线段截止,重新计算生成新的线段,基于实验将其设定为1个像素误差
5、实验
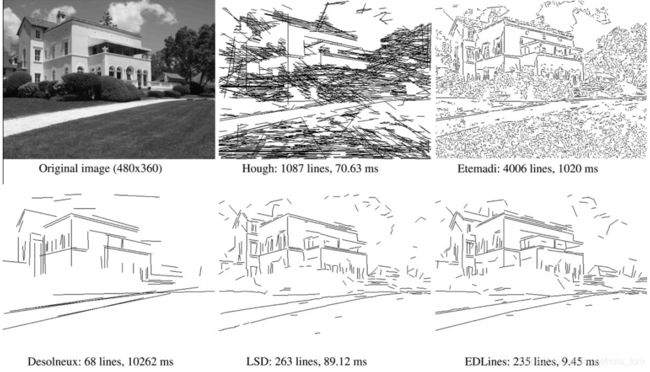
EDLines在保证与LSD质量相近的同时,其速度为LSD的十倍左右
同时非常好的保留了图像的信息,比Hough等好很多