图卷积神经网络学习笔记

前言

这篇文章是作者在初次接触学习GNN/GCN的过程中为了方便理解而记录下的个人笔记，主要参考了这个问题下诸路大神们的解答。笔记将从尽量宏观的角度来切入图神经网络，然后由浅入深，分享在这里希望同时也能对一起初入这个领域的朋友们有一点帮助。

整体看待

从卷积、CNN、GCN的关系来切入

要了解GCN/GNN的现实意义就必须对CNN有一个基本的了解。从宏观意义上来看，不论是GCN/GNN或是CNN，实际上都是将现实生活中的高维数据通过数学手段处理，在保留数据关键特征的情况下将其降至人类可以直观理解的维度。

为了便于理解，我们以身份证号码为例。假设我们的目的是判断身份证号码持有者的性别，也就是说我们要把一维向量的身份证号码通过数学手段变换为0维的数字$\{x|x=0,1\}$，这也就是特征提取。在这个例子中，我们是造物者，我们创造了身份证的编码方式，因此我们自然知道身份证的17个数字中16个与我们关注的性别这一关键特征毫无关系，从而我们很容易就得到了特征提取的具体手段。但在自然界当中，当我们不再是造物者时，这个特征提取的具体手段就成为困扰我们解决这类问题的瓶颈。

在上个世纪，许多领域的研究都面临着类似的问题，研究者们的不懈努力和聪明才智使得他们开发出了很多针对各类问题的特征提取处理手段，例如NLP的Ngram，语音识别中的MFCC和HMM，以及图像识别中一些简易的用于平滑或者做边缘检测的卷积核。这些手段的开发往往都结合了专家们对这一领域的多年研究，这样的代价实在是太高。而CNN为代表的一类方法的出现则消解了这个问题，它通过利用计算机的计算能力，用一套统一的数学方法进行迭代计算，从而逼近理想的特征提取方法。

但如此去逼近特征提取方法的手段是有限制的。这个手段当中很重要的一环就是卷积核，一个卷积核通常为大小$n\times n$的矩阵，$n$的大小视实际情况而定。而卷积核与源数据进行卷积运算可以提取到源数据的特征。在此我们不细究卷积运算的细节，但有一点是肯定的。卷积核作为矩阵，与其进行卷积计算的源数据也应该是一个矩阵。 这在现实中意味着这类特征提取手段只能适应规规整整的数据，例如rgb三通道图片，灰度图片。我们会发现符合这一条件的最主要的数据就是图片，而事实也是如此，直接简单利用卷积作为特征提取手段的正是图片识别这一领域。而语音识别和自然语言处理等方面的数据还要结合其他手段。

从上述内容看来，对于数据的特征提取问题，上世纪研究者的研究是针对具体问题的特解；CNN则是在欧几里得数据中的通解。那么下文介绍的GCN则对应了任意拓扑结构的解。这里的拓扑结构在现实生活中可以是人际关系网，蛋白质结构等等，这使得卷积能处理的数据类型更加的广泛。

GNN与GCN的关系

通常所说的图神经网络(GNN)是一个比较宽泛的概念，在2013年GCN被提出之前，GNN代表的是一类利用压缩映射来迭代式更新，最终收敛到结果的一种图神经网络算法。GCN提出后，图神经网络包含了GNN和GCN，它们之间的关系类似于DNN与CNN的关系。

图的特征

GCN或GNN中的G都是指Graph，因此对图有基本的了解是必须的。

图的特征分析

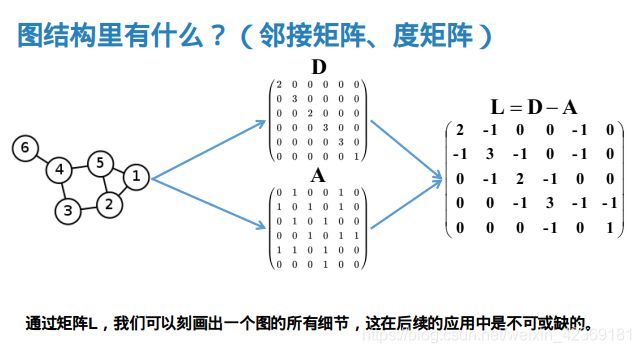
在图神经网络中，我们研究的图往往如上图所示，它有顶点(Vertex)集$V=\{x_i\}$，边(Edge)集$E=\{x_{(i,j)}\}$。它可以表示为$G(V,E)$的形式。

为了表示它顶点之间的连接关系，我们通常通过邻接矩阵$A=\{a_{ij}\}$的形式来表示。其中$a_{ij}=1$代表第$i$个顶点与第$j$个顶点相连；$a_{jk}=0$代表第$j$个顶点与第$k$个顶点不相连。对于无向图而言，邻接矩阵显然是对称矩阵。

此外我们记每个顶点的边的数量为该顶点的度(degree)，与之对应的有一个度矩阵$D=\{d_{ij}\}$，其中$d_{ii}$的值为第$i$个顶点的度数，其余元素都为$0$。

通过上述的量，我们可以刻画出一个图的所有细节，这在后续的应用中是不可或缺的。

特征提取方式

图的特征提取方式主要分成spatial和spectral两类，而GCN主要是spectral方法，因此我们只介绍这类方法。

spectral domain

spectral方法是GCN的理论基础，在上一个Part中我们提到GCN是CNN在拓扑数据中的抽象，而spectral就是完成这个迁移的基本方法。以下的介绍是基于对文章引用链接以及文章引用链接的理解和自我梳理。

首先我们先看看基于上文定义的图的基本特征可以得到什么。为了方便理解，这里引用文章的视角，从热传递的角度来看待图的特征。截取关键的部分：假设每个节点都有初始温度，并且相连的节点之间热量流动的速度满足牛顿冷却定律，即对于任意一点$x_i$，其温度随时间的变化可以用以下式子来刻画：
$$\frac{d{T}_i}{t}=-k\sum _j{a}_{ij}(T_i-T_j)$$

上述式子的物理意义即温度的变化速度正比于该点与周围节点的温度差。那么通过变形我们可以得到：
$$\frac{d{T}_i}{t}=-k(T_i\sum _j{a}_{ij}-\sum _j{a}_{ij}{T}_j)=-k(T_i{d}_{ii}-\sum _j{a}_{ij}{T}_j)$$

其中$d_{ii}$即为顶点$i$的度数。将上方式子写为向量形式，定义$T=[T_1,T_2,\cdots ,T_n{]}^T$，则有：
$$\frac{dT}{dt}=-kDT+kAT=-k(D-A)T$$

上式的物理意义可以解释为：途中每个顶点的温度随时间的变化取决于两个因素：

• 1.图的结构特征$(D-A)$。
• 2.顶点本身的值$T$。

而在GCN中，我们正是使用$L=D-A$，又称为拉普拉斯矩阵，来刻画图本身的结构特征。若从更宽泛的意义上来解读$L$与$T$，可以说每个顶点上的值不再是热量，而可以是代表该顶点的某个特征的值，而$L$刻画的则是该值在图中传播的模式。由此我们正式开始介绍GCN的特征提取方式。

GCN的特征提取方式

从拉普拉斯矩阵的特征分解开始

由于$D$与$A$均为对称矩阵，所以$L$也是对称矩阵，这使得拉普拉斯矩阵的特征分解可以写为特殊的形式：
$$L=Udiag({\lambda }_i)U^T$$

其中$U=(u_1,u_2,\cdots ,u_n)$，列向量$u_i$是特征值${\lambda }_i$对应的特征向量。且有$U{U}^T=I$。

Graph上的傅里叶变换

由于拉普拉斯矩阵是对称矩阵，因此它有n个线性无关的特征向量并且相互正交。在$n$个顶点的Graph$(n\times n)$空间中，我们以这n个特征向量为基。有：
$$Lu=\lambda u$$

传统的傅里叶变换中，将信号由时域变换到频域的公式为：
$$F(w)=\int f(t)e^{-iwt}dt$$

其本质是使用$e^{-iwt}$(即拉普拉斯算子的特征函数)作为该变换的卷积核，将$w$为特征值(即频率)的信号在时间上求积分从而得到$w$对应的在频率域上的值。而对于图而言，拉普拉斯矩阵对应拉普拉斯算子，特征值${\lambda }_i$对应频率$w$，特征向量$u_i$对应特征函数$e^{-iwt}$。从而我们可以定义Graph上的傅里叶变换为：
$$F({\lambda }_i)=\sum _{k=1}^{n}f(k)u_i^{\ast }(k)$$

其中$f(k)$即对应傅里叶变换中的源信号，在上文中，它也指顶点的值$T_i$。总而言之，它是外界输入的特征。将上式推广为全图的矩阵形式，令$\lambda =\{{\lambda }_i\}$，$\hat{f}(\lambda )=(F({\lambda }_1),F({\lambda }_2),\cdots ,F({\lambda }_n){)}^T$，$f=(f(1),f(2),\cdots ,f(n){)}^T$，那么：
$$\hat{f}=U^{T}f$$

类似的，传统的傅里叶逆变换中，我们通过对频率$w$求积分来还原信号值：
$$f(t)=\frac{1}{2\pi }\int F(w)e^{iwt}dw$$

对应的在图中我们可以对特征值${\lambda }_i$求和得到对应的$f(i)$：
$$f(i)=\sum _{k=1}^{n}F({\lambda }_k)u_k(i)$$

推广为矩阵形式：
$$f=U\hat{f}$$

Graph上的卷积定理

在傅里叶变换中，有函数的卷积的傅里叶变换等于函数的傅里叶变换的乘积，即：
$$f(t)\ast h(t)=\frac{1}{2\pi }\int \hat{f}(w)\hat{h}(w)e^{iwt}dw$$

那么迁移到Graph上，利用上节的结论我们可以得到：
$$(f\ast h{)}_G=U((U^{T}f)\odot (U^{T}h))$$

上式即为Graph上的卷积定理，在文章引用链接中，作者为了方便后续理解第一代GCN卷积核的结构，将上述卷积公式等价变换为如下形式：
$$(f\ast h{)}_G=Udiag(\hat{h}({\lambda }_i))U^{T}f$$

第一类GCN卷积核

在文章Spectral Networks and Locally Connected Networks on Graphs中，作者将原来的卷积定理中的$\hat{h}({\lambda }_i)$替换为${\theta }_i$，即：
$$y_{output}=\sigma (Udiag({\theta }_i)U^{T}x)$$

第二类GCN卷积核

在文章Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering中，作者把$\hat{h}({\lambda }_i)$换为${\sum }_{j=0}^k{\alpha }_j{\lambda }_i^j$，因为原矩阵为对角矩阵，因此可以写为：
$$diag(\sum _{j=0}^k{\alpha }_j{\lambda }_i^j)=\sum _{j=0}^k{\alpha }_{j}diag({\lambda }_i^j)$$

从而有：
$$y_{output}=\sigma (U\sum _{j=0}^k{\alpha }_{j}diag({\lambda }_i^j)U^{T}x)=\sigma (\sum _{j=0}^k{\alpha }_{j}Udiag({\lambda }_i^j)U^{T}x)=\sigma (\sum _{j=0}^{k-1}{\alpha }_j{L}^{j}x)$$

第三类GCN卷积核(Chebyshev)

与第二类类似，使用Chebyshev多项式代替卷积核：
$$diag(\cdot ):=\sum _{j=0}^{K-1}{\beta }_j{T}_j(\widehat{diag}({\lambda }_i))$$

其中$\widehat{diag}({\lambda }_i)=2diag({\lambda }_i)/{\lambda }_{max}-I$，是为了满足切比雪夫多项式的定义域$[-1,1]$的要求，而切比雪夫多项式本身的定义为$T_k(x)=cos(k\cdot arccos(x))$。于是有：
$$y_{output}=\sigma (U\sum _{j=0}^{K-1}{\beta }_j{T}_j(\widehat{diag}({\lambda }_i))U^{T}x)=\sigma (\sum _{j=0}^{K-1}{\beta }_j{T}_j(U\widehat{diag}({\lambda }_i)U^T)x)=\sigma (\sum _{j=0}^{K-1}{\beta }_j{T}_j(\hat{L})x)$$

后记

到此为止我才刚刚在图卷积神经网络的这个领域沾了沾水，上述内容如果有错欢迎指正(在此先谢过各位)，一起继续学习吧～