33. 多输入多输出通道 代码实现

1. 多输入通道

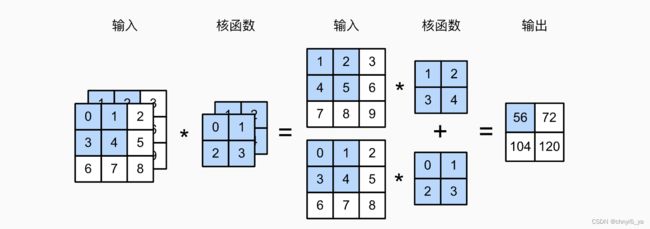
实现一下多输入通道互相关运算。 简而言之，我们所做的就是对每个通道执行互相关操作，然后将结果相加。

import torch
from d2l import torch as d2l

def corr2d_multi_in(X,K):
    return sum(d2l.corr2d(x,k) for x,k in zip(X,K))

关于python中的zip（）函数

构造图中所示的张量X和K：

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)

运行结果：

2. 多输出通道

实现一个计算多个通道的输出的互相关函数。

def corr2d_multi_in_out(X, K):# K是4维的，最外面一维是输出通道
    # 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算。
    # 最后将所有结果都叠加在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
    # 对每一个大K拿出一个小k，小k是3d的tensor

torch.stack()的详细解释

通过将核张量K与K+1（K中每个元素加1）和K+2连接起来，构造了一个具有3个输出通道的卷积核。

# 之前的K是一个3d的tensor
K = torch.stack((K, K + 1, K + 2), 0)
K.shape # 在新创建的第4维上把3个3维的tensor堆叠起来

运行结果如下：

下面，我们对输入张量X与卷积核张量K执行互相关运算。现在的输出包含3个通道，第一个通道的结果与先前输入张量X和多输入单输出通道的结果一致。

corr2d_multi_in_out(X, K)

3. 1 * 1 卷积 等价于全连接

下面，我们使用全连接层实现1 * 1卷积。 请注意，我们需要对输入和输出的数据形状进行调整。

def corr2d_multi_in_out_lx1(X,K):
    c_i,h,w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i,h * w))
    K = K.reshape((c_o,c_i))
    Y = torch.matmul(K,X)  # 全连接层中的矩阵乘法
    return Y.reshape((c_o,h,w))

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_lx1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6