机器学习算法系列(一)- 感知器学习算法(PLA)
阅读本文需要的背景知识点:数学基础知识、一丢丢编程知识
一、引言
前面一节我们了解了机器学习算法系列(〇)- 基础知识,接下来正式开始机器学习算法的学习,首先我们从最简单的一个算法——感知器学习算法(Perceptron Learning Algorithm)开始。
我们在使用电子邮件时,应该注意到现代邮箱都有反垃圾邮件的功能,系统根据邮件的内容自动判断是否是垃圾邮件,节省了我们的时间,试想一下这个功能应该如何实现呢?
我们可以先收集一批邮件,总结出对判断是否是垃圾邮件有用的一些特征值(例如:邮件是否包含链接、邮件出现过多少个营销词语、邮件的发送时间等等),然后对每一封邮件先人工的判断是否是垃圾邮件,最后试图通过这些数据来找到里面所包含的关联关系。以后给到一封新邮件的时候,我们就可以通过这些关系来判断是否是垃圾邮件了。
二、模型介绍
回想一下在初中生物教材上介绍过的神经细胞,它是由树突、轴突、突触和细胞体组成的结构体。神经细胞是否激活并输出电信号是由其接收到的输入信号量和突触的强度所决定的,当其总和超过某个阈值时,细胞体就会激动并输出电信号。由这一神经细胞的行为,人们提出了感知器的概念和对应的感知器学习算法。
感知器1(Perceptron)是一种二元线性分类器,将一个线性可分的数据集通过线性组合分成两种类型。在人工神经网络领域中,感知机也被指为单层的人工神经网络。
几何意义:在二维平面内找到一条直线将两种类型的数据完全分开。在高维空间里为找到一个超平面将两类数据分开。

数学定义:把矩阵上的输入 X(实数值向量)映射到输出值 h(x) 上(一个二元的值 -1 或 +1 )。假设存在 d 个 x ,通过 w 的加权求和,大于某个临界值时返回 +1,小于某个临界值时返回 -1。
∑ i = 1 d w i x i > 临界值 + 1 ( A 分类 ) ∑ i = 1 d w i x i < 临界值 − 1 ( B 分类 ) \begin{array}{cc} \sum_{i=1}^{d} w_{i} x_{i}>\text { 临界值 } & +1(A \text { 分类 }) \\ \sum_{i=1}^{d} w_{i} x_{i}<\text { 临界值 } & -1(B \text { 分类 }) \end{array} ∑i=1dwixi> 临界值 ∑i=1dwixi< 临界值 +1(A 分类 )−1(B 分类 )
将上式写成一个函数的形式(sign函数称为符号函数2,当输入小于 0 则输出 -1,当输入大于 0 则输出 +1)
h ( x ) = sign ( ∑ i = 1 d w i x i − 临 界 值 ) h(x) = \operatorname{sign}\left(\sum_{i = 1}^dw_ix_i - 临界值\right) h(x)=sign(i=1∑dwixi−临界值)
将负的临界值当作第 0 个 w,正1 当作第 0 个 x
h ( x ) = sign ( ( ∑ i = 1 d w i x i ) + ( − 临界值 ) ⏟ w 0 ⋅ ( + 1 ) ⏟ x 0 ) h(x)=\operatorname{sign}(\left(\sum_{i=1}^{d} w_{i} x_{i}\right)+\underbrace{(-\text { 临界值 })}_{w_{0}} \cdot \underbrace{(+1)}_{x_{0}}) h(x)=sign((i=1∑dwixi)+w0 (− 临界值 )⋅x0 (+1))
可将临界值合到从 1 到 d 的连加运算中,则连加运算的下界变为 0
h ( x ) = sign ( ∑ i = 0 d w i x i ) h(x) = \operatorname{sign}\left(\sum_{i=0}^dw_ix_i\right) h(x)=sign(i=0∑dwixi)
最后函数可改写为两个向量(w、x)的点积形式
h ( x ) = sign ( w T x ) h(x) = \operatorname{sign}\left( w^Tx \right) h(x)=sign(wTx)
感知器是一种特别简单的线性分类模型,但是它的本质缺陷是不能处理线性不可分的问题,后面的小节将介绍一个可以允许存在一些错误的发生,能处理线性不可分数据集的算法——口袋算法(Pocket Algorithm)
三、算法步骤
感知器学习算法(Perceptron Learning Algorithm)- 其核心思想就是以错误为驱动,逐步修正错误最后收敛的过程。
初始化向量 w,例如 w 初始化为零向量
循环 t = 0,1,2 …
按顺序或随机遍历全部数据并计算 h(x) ,直到找到其中一个数据的 h(x) 与目标值 y 不符
sign ( w t T x n ( t ) ) ≠ y n ( t ) \operatorname{sign}\left(w_{t}^{T} x_{n(t)}\right) \neq y_{n(t)} sign(wtTxn(t))=yn(t)
修正向量 w
w t + 1 ← w t + y n ( t ) x n ( t ) w_{t+1} \leftarrow w_{t}+y_{n(t)} x_{n(t)} wt+1←wt+yn(t)xn(t)
直到全部数据的结果都没有错误退出循环,所得的 w 即为一组方程的解
四、原理证明
假设最后的目标权重系数为 w f w_f wf,待优化的权重系数为 w w w。通过单位 w f w_f wf 与单位 w w w 的点积来作为两个向量是否靠近的标准。(两个单位向量的点积越大,说明两个向量越接近,当两个向量同向并共线时两者的点积最大)
由于目标权重系数 w f w_f wf 的全部分类都是正确的,所以每一个数据点计算出的值与目标值的乘积必然大于乘积中的最小值,并且大于 0(分类正确即同号)
y n ( t ) w f T x n ( t ) ≥ min n y n w f T x n > 0 y_{n(t)} w_{f}^{T} x_{n(t)} \geq \min _{n} y_{n} w_{f}^{T} x_{n}>0 yn(t)wfTxn(t)≥nminynwfTxn>0
待优化的权重系数为 w 只在数据集分类错误的时候做更新,所以在该数据点计算出的值与目标值的乘积必然小于等于 0(分类错误即异号)
sign ( w t T x n ( t ) ) ≠ y n ( t ) ⇔ y n ( t ) w t T x n ( t ) ≤ 0 \operatorname{sign}\left(w_{t}^{T} x_{n(t)}\right) \neq y_{n(t)} \Leftrightarrow y_{n(t)} w_{t}^{T} x_{n(t)} \leq 0 sign(wtTxn(t))=yn(t)⇔yn(t)wtTxn(t)≤0
权重系数更新规则
w t = w t − 1 + y n ( t ) x n ( t ) w_{t}=w_{t-1}+y_{n(t)} x_{n(t)} wt=wt−1+yn(t)xn(t)
由上面的三个公式可以得到目标权重系数与待优化的权重系数的点积的一个下界:
(1)将公式三带入可得
(2)展开后,使用公式一将第二项替换
(3)经过 T 轮更新后,必然大于等于 w 0 + T w_0 + T w0+T 个最小值
(4)初始的权重系数为零向量
w f T w t = w f T ( w t − 1 + y n ( t − 1 ) x n ( t − 1 ) ) ≥ w f T w t − 1 + min n y n w f T x n ≥ … ≥ w 0 + T ⋅ min n y n w f T x n ≥ T ⋅ min n y n w f T x n \begin{aligned} w_{f}^{T} w_{t} &=w_{f}^{T}\left(w_{t-1}+y_{n(t-1)} x_{n(t-1)}\right) \\ & \geq w_{f}^{T} w_{t-1}+\min _{n} y_{n} w_{f}^{T} x_{n} \\ & \geq \ldots \\ & \geq w_{0}+T \cdot \min _{n} y_{n} w_{f}^{T} x_{n} \\ & \geq T \cdot \min _{n} y_{n} w_{f}^{T} x_{n} \end{aligned} wfTwt=wfT(wt−1+yn(t−1)xn(t−1))≥wfTwt−1+nminynwfTxn≥…≥w0+T⋅nminynwfTxn≥T⋅nminynwfTxn
由上面的三个公式可以得到待优化的权重系数模的平方的一个上界:
(1)将公式三带入可得
(2)展开平方式
(3)中间一项由公式二可知必然小于等于 0,所以可以化简
(4)由于目标值 y 只有 +1 与 -1 ,所以平方必然为 1,每一个数据点模的平方必然小于等于最大的数据点模的平方
(5)经过 T 轮更新后,必然小于等于 w 0 w_0 w0 模的平方 + T 个最大的数据点模的平方
(6)初始的权重系数模的平方为 0
∥ w t ∥ 2 = ∥ w t − 1 + y n ( t − 1 ) x n ( t − 1 ) ∥ 2 = ∥ w t − 1 ∥ 2 + 2 y n ( t − 1 ) w t − 1 T x n ( t − 1 ) + ∥ y n ( t − 1 ) x n ( t − 1 ) ∥ 2 ≤ ∥ w t − 1 ∥ 2 + 0 + ∥ y n ( t − 1 ) x n ( t − 1 ) ∥ 2 ≤ ∥ w t − 1 ∥ 2 + max n ∥ x n ∥ 2 ≤ … ≤ ∥ w 0 ∥ 2 + T ⋅ max n ∥ x n ∥ 2 ≤ T ⋅ max n ∥ x n ∥ 2 \begin{aligned} \left\|w_{t}\right\|^{2} &=\left\|w_{t-1}+y_{n(t-1)} x_{n(t-1)}\right\|^{2} \\ &=\left\|w_{t-1}\right\|^{2}+2 y_{n(t-1)} w_{t-1}^{T} x_{n(t-1)}+\left\|y_{n(t-1)} x_{n(t-1)}\right\|^{2} \\ & \leq\left\|w_{t-1}\right\|^{2}+0+\left\|y_{n(t-1)} x_{n(t-1)}\right\|^{2} \\ & \leq\left\|w_{t-1}\right\|^{2}+\max _{n}\left\|x_{n}\right\|^{2} \\ & \leq \ldots \\ & \leq\left\|w_{0}\right\|^{2}+T \cdot \max _{n}\left\|x_{n}\right\|^{2} \\ & \leq T \cdot \max _{n}\left\|x_{n}\right\|^{2} \end{aligned} ∥wt∥2=∥∥wt−1+yn(t−1)xn(t−1)∥∥2=∥wt−1∥2+2yn(t−1)wt−1Txn(t−1)+∥∥yn(t−1)xn(t−1)∥∥2≤∥wt−1∥2+0+∥∥yn(t−1)xn(t−1)∥∥2≤∥wt−1∥2+nmax∥xn∥2≤…≤∥w0∥2+T⋅nmax∥xn∥2≤T⋅nmax∥xn∥2
由上面两个推导结果可知单位 w f w_f wf 与单位 w w w 的点积的下界
(1)带入上面两个推导结果可得
(2)化简提出唯一一个变量
(3)由于第二个乘数里面所有项都是常数且都为正数,所以单位 w f w_f wf 与单位 w w w 的点积的下界只与循环次数 T 有关
w f T ∥ w f ∥ w t ∥ w t ∥ ≥ T ⋅ min n y n w f T x n ∥ w f ∥ T ⋅ max n ∥ x n ∥ 2 ≥ T ⋅ min n y n w f T x n ∥ w f ∥ max n ∥ x n ∥ 2 ≥ T ⋅ 常数 \begin{aligned} \frac{w_{f}^{T}}{\left\|w_{f}\right\|} \frac{w_{t}}{\left\|w_{t}\right\|} & \geq \frac{T \cdot \min _{n} y_{n} w_{f}^{T} x_{n}}{\left\|w_{f}\right\| \sqrt{T \cdot \max _{n}\left\|x_{n}\right\|^{2}}} \\ & \geq \sqrt{T} \cdot \frac{\min _{n} y_{n} w_{f}^{T} x_{n}}{\left\|w_{f}\right\| \sqrt{\max _{n}\left\|x_{n}\right\|^{2}}} \\ & \geq \sqrt{T} \cdot \text { 常数 } \end{aligned} ∥wf∥wfT∥wt∥wt≥∥wf∥T⋅maxn∥xn∥2T⋅minnynwfTxn≥T⋅∥wf∥maxn∥xn∥2minnynwfTxn≥T⋅ 常数
由上面的结论可知,当循环次数增大时,点积越大,说明两个单位向量越接近。而由于单位向量的点积最大为 1,说明循环次数 T 存在一个上界,所以算法最后会停下来。
五、代码实现
使用 Python 实现 PLA:
import numpy as np
def pla(X, y):
"""
感知器学习算法实现
注意:只能处理线性可分的数据集,输入线性不可分的数据集函数将无法停止
args:
X - 训练数据集
y - 目标标签值
return:
w - 权重系数
"""
done = False
# 初始化权重系数
w = np.zeros(X.shape[1])
# 循环
while(done == False):
done = True
# 遍历训练数据集
for index in range(len(X)):
x = X[index]
# 判定是否与目标值不符
if x.dot(w) * y[index] <= 0:
done = False
# 修正权重系数
w = w + y[index] * x
return w
六、第三方库实现
scikit-learn3实现:
from sklearn.linear_model import Perceptron
# 初始化感知器
clf = Perceptron()
# 用随机梯度下降拟合线性模型
clf.fit(X, y)
# 权重系数
w = clf.coef_
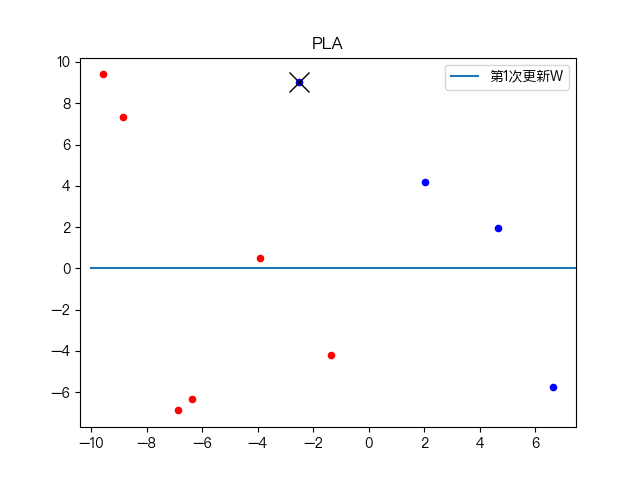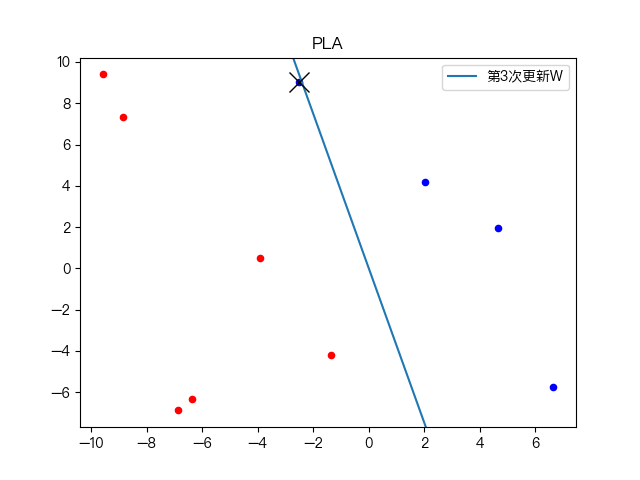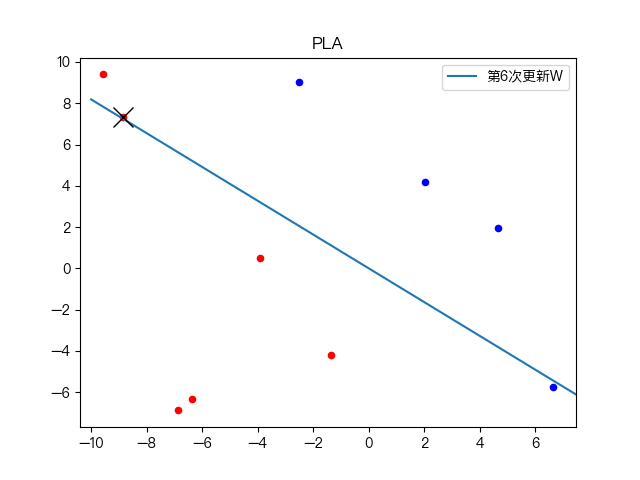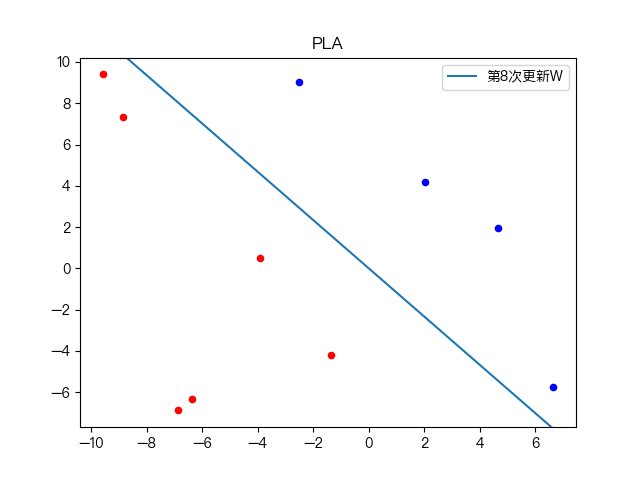
七、示例演示
八、思维导图
九、参考文献
- https://zh.wikipedia.org/wiki/%E6%84%9F%E7%9F%A5%E5%99%A8
- https://zh.wikipedia.org/wiki/%E7%AC%A6%E5%8F%B7%E5%87%BD%E6%95%B0
- https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注