数字信号处理中的过采样

1.过采样可以更真实的重建原始信号
2.采样系统中，利用过采样可以提升采样分辨率
3.欠采样信号会失真
4.要理解过采样的意义，首先建议理解什么是采样定理，什么是欠采样等概念什么是过采样？

在信号处理中，过采样是指以明显高于奈奎斯特速率的采样频率对信号进行采样。 从理论上讲，如果以奈奎斯特速率或更高的速率进行采样，则可以完美地重建带宽受限的信号。 奈奎斯特频率定义为信号带宽的两倍。 过采样能够提高分辨率和信噪比SNR，并且通过放宽抗混叠滤波器的性能要求，有助于避免混叠和相位失真。在很多项目应用中，需要测量信号的动态范围较大，且需要参数的微小变化。例如，ADC需要测量很大的温度范围（比如工业中甚至要求从-200℃~500℃），但仍要求系统对小于1度的变化做出响应。 常见的单片机片上ADC位数为12位，如要实现高于12位分辨率要怎么做呢？我们知道奈奎斯特-香农采样定理可知：

$f_n=2\times f_m$
其中：

$f_m$为输入待采样信号最高频率
$f_n$为奈奎斯特频率。

如果实际采样频率高于奈奎斯特频率$f_n$，即为过采样。那么低于奈奎斯特采样频率进行采样就称为欠采样，如下图：

或许你会问，常规的应用都是过采样，怎么也没见分辨率提高了呀？如果仅仅过采样，要实现更高分辨率显然是不够的，那么要怎么利用过采样实现更高的分辨率呢？要知道所采用的ADC硬件核分辨率是固定的，难道还会变不成.

过采样提高分辨率
如果对一模拟信号，采用过采样，然后再进行一定的软件后处理，理论上是可以得到更高分辨率的：

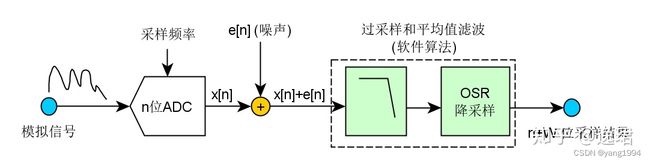
为增加有效位数（ENOB ：effective number of bits），对信号进行过采样，所需的过采样率可以由下面公式确定（省略理论推导，过于枯燥）：
$f_{os}=4^W\times f_s$

其中：

$f_{os}$为过采样频率
$f_s$产品所需实际采样频率
$W$ 为额外所需增加的分辨率位数

假设系统使用12位ADC每100 ms输出一次采样值也即(10 Hz)。 为了将测量的分辨率提高到16位，我们按上述公式计算过采样频率：
$f_{os}=4^W\times f_s=4^4\times 10=2560Hz$

因此，如果我们以fs=2560Hzf_s=2560 Hzf_s=2560 Hzf对信号进行过采样，然后在所需的采样周期内收集足够的样本以对它们进行平均，现在可以将16位输出数据用于16位测量。具体怎么做呢？
首先将256个连续采样累加，然后将总数除以16（或将总数右移4位）。 该过程通常称为抽取，也即将速率采样。在类似进行下一次16位样本处理。注意：用于累积过采样数据并执行除法的内存及数据类型必须具有足够的字节，以防止溢出和截断错误。比如这里累积和可以采样32位无符号整型。由上面公式可得出一个重要结论：每提高W位分辨率，需要提高采样率$4^W$ 倍。

过采样提高ADC的信噪比
ADC测量的SNR理论极限基于量化噪声，这是基于在没有过采样和平滑滤波情况下模数转换过程中固有的量化误差所致。 而量化误差取决于ADC分辨率的位数，其中N为ADC的位数，$V_{ref}$为参考电压。

$\Delta =\frac{V_{ref}}{2^N}$

SNR理论情况下极限值的计算方式是数据转换的有效位数，如下所示：
SNR(dB)=(6.02XENOB) + 1.76
这个公式没必要去记，用到的时候参考计算一下即可。从公式中可看出，要提升一个模数转换器的理论SNR的一种可行方案可以通过提升采样位数，但是需要注意的是这里的信噪比是度量模数转换器本身的，就一个真实系统的信噪比还与整个信号链相关！从上式中不难算出，12位ADC的理论SNR极限值为74dB,而通过过采样提升4位分辨率后，其SNR理论极限提高至96 dB！