Pytorch 卷积核填充和步幅、多输入多输出通道、池化层
Pytorch 卷积层里的填充和步幅
0. 环境介绍
环境使用 Kaggle 里免费建立的 Notebook
教程使用李沐老师的 动手学深度学习 网站和 视频讲解
小技巧:当遇到函数看不懂的时候可以按 Shift+Tab 查看函数详解。
1. 填充(padding)和步幅(stride)
注:CNN 可视化网站:https://poloclub.github.io/cnn-explainer/
1.1 填充(padding)
假设以下情景: 有时,在应用了连续的卷积之后,我们最终得到的输出远小于输入大小。这是由于卷积核的宽度和高度通常大于 1 1 1 所导致的。
比如,一个 240 × 240 240 \times 240 240×240 像素的图像,经过 10 10 10 层的 5 × 5 5 \times 5 5×5 卷积后,将减少到 200 × 200 200 \times 200 200×200 像素。如此一来,原始图像的边界丢失了许多有用信息。而填充是解决此问题最有效的方法。
在输入图像的边界填充元素(一般为 0 0 0)。
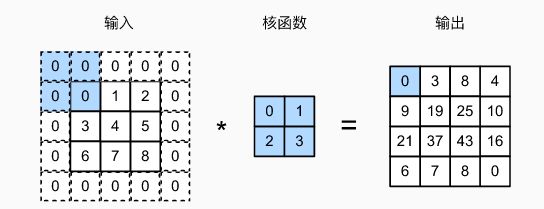
填充 p h p_h ph 行和 p w p_w pw 列,输出形状为:
( n h − k h + p h + 1 ) × ( n w − k w + p w + 1 ) (n_h-k_h+p_h+1)\times(n_w-k_w+p_w+1) (nh−kh+ph+1)×(nw−kw+pw+1)
通常取 p h = k h − 1 p_h=k_h-1 ph=kh−1, p w = k w − 1 p_w=k_w-1 pw=kw−1,使输入图像形状经过与卷积核运算后输出形状保持一致。
- 当 k h k_h kh 为奇数:在上下两侧填充 p h / 2 p_h/2 ph/2
- 当 k h k_h kh 为偶数:在上侧填充 ⌈ p h / 2 ⌉ \left\lceil p_{h} / 2\right\rceil ⌈ph/2⌉,在下侧填充 ⌊ p h / 2 ⌋ \left\lfloor p_{h} / 2\right\rfloor ⌊ph/2⌋
注:卷积神经网络中卷积核的高度和宽度通常为奇数,例如1、3、5或7。 选择奇数的好处是,保持空间维度的同时,我们可以在顶部和底部填充相同数量的行,在左侧和右侧填充相同数量的列。
1.2 步幅(stride)
有时,我们可能希望大幅降低图像的宽度和高度。例如,如果我们发现原始的输入分辨率十分冗余。步幅则可以在这类情况下提供帮助。
卷积窗口从输入张量的左上角开始,向下、向右滑动,默认情况下都是滑动的步幅是 1 1 1 个像素。
给定高度 s h s_h sh 和宽度 s w s_w sw 的步幅,输出形状是:
- ⌊ ( n h − k h + p h + s h ) / s h ⌋ × ⌊ ( n w − k w + p w + s w ) / s w ⌋ \lfloor(n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor(n_w-k_w+p_w+s_w)/s_w\rfloor ⌊(nh−kh+ph+sh)/sh⌋×⌊(nw−kw+pw+sw)/sw⌋
如果 p h = k h − 1 p_h=k_h-1 ph=kh−1, p w = k w − 1 p_w=k_w-1 pw=kw−1
- ⌊ ( n h + s h − 1 ) / s h ⌋ × ⌊ ( n w + s w − 1 ) / s w ⌋ \left\lfloor\left(n_{h}+s_{h}-1\right) / s_{h}\right\rfloor \times\left\lfloor\left(n_{w}+s_{w}-1\right) / s_{w}\right\rfloor ⌊(nh+sh−1)/sh⌋×⌊(nw+sw−1)/sw⌋
如果输出高度和宽度可以被步幅整除
- ( n h / s h ) × ( n w / s w ) \left(n_{h} / s_{h}\right) \times\left(n_{w} / s_{w}\right) (nh/sh)×(nw/sw)
填充和步幅是卷积层的超参数。
1.3 代码实现
1.3.1 填充
import torch
from torch import nn
# 为了方便起见,我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重,并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
# 这里的(1,1)表示批量大小和通道数都是1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
# 省略前两个维度:批量大小和通道
return Y.reshape(Y.shape[2:])
# 请注意,这里每边都填充了1行或1列,因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape
![]()
用公式 ( n h − k h + p h + 1 ) × ( n w − k w + p w + 1 ) (n_h-k_h+p_h+1)\times(n_w-k_w+p_w+1) (nh−kh+ph+1)×(nw−kw+pw+1) 计算:
( 8 − 3 + 2 + 1 ) × ( 8 − 3 + 2 + 1 ) = ( 8 × 8 ) (8 - 3 + 2 + 1) \times (8 - 3 + 2 + 1) = (8 \times 8) (8−3+2+1)×(8−3+2+1)=(8×8)
注:(1, 1) + (8, 8) = (1, 1, 8, 8)

# 卷积核为 5*3, padding 上下两侧为 2, 共 4, 左右两侧为 1, 共 2
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape
![]()
用公式 ( n h − k h + p h + 1 ) × ( n w − k w + p w + 1 ) (n_h-k_h+p_h+1)\times(n_w-k_w+p_w+1) (nh−kh+ph+1)×(nw−kw+pw+1) 计算:
( 8 − 5 + 4 + 1 ) × ( 8 − 3 + 2 + 1 ) = ( 8 × 8 ) (8-5+4+1)\times(8-3+2+1)=(8\times8) (8−5+4+1)×(8−3+2+1)=(8×8)
1.3.2 步幅
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape
![]()
用公式 ⌊ ( n h − k h + p h + s h ) / s h ⌋ × ⌊ ( n w − k w + p w + s w ) / s w ⌋ \lfloor(n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor(n_w-k_w+p_w+s_w)/s_w\rfloor ⌊(nh−kh+ph+sh)/sh⌋×⌊(nw−kw+pw+sw)/sw⌋ 计算:
( ⌊ ( 8 − 3 + 2 + 2 ) / 2 ⌋ ) × ( ⌊ ( 8 − 3 + 2 + 2 ) / 2 ⌋ ) = ( 4 × 4 ) (\lfloor(8-3+2+2)/2\rfloor) \times (\lfloor(8-3+2+2)/2\rfloor) = (4 \times 4) (⌊(8−3+2+2)/2⌋)×(⌊(8−3+2+2)/2⌋)=(4×4)
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape
![]()
用公式 ⌊ ( n h − k h + p h + s h ) / s h ⌋ × ⌊ ( n w − k w + p w + s w ) / s w ⌋ \lfloor(n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor(n_w-k_w+p_w+s_w)/s_w\rfloor ⌊(nh−kh+ph+sh)/sh⌋×⌊(nw−kw+pw+sw)/sw⌋ 计算:
( ⌊ ( 8 − 3 + 0 + 3 ) / 3 ⌋ ) × ( ⌊ ( 8 − 5 + 2 + 4 ) / 4 ⌋ ) = ( 2 × 2 ) (\lfloor(8-3+0+3)/3\rfloor) \times (\lfloor(8-5+2+4)/4\rfloor) = (2 \times 2) (⌊(8−3+0+3)/3⌋)×(⌊(8−5+2+4)/4⌋)=(2×2)
默认情况下,填充为 0 0 0,步幅为 1 1 1。在实践中,我们很少使用不一致的步幅或填充,也就是说,我们通常设置 p h = p w p_h = p_w ph=pw 和 s h = s w s_h = s_w sh=sw。
2. 多输入多输出通道
2.1 多输入通道
每个 RGB 输入图像具有 3 × h × w 3\times h\times w 3×h×w 的形状。我们将这个大小为 3 3 3 的轴称为通道(channel)维度。
- 输入 X X X: c i × n h × n w c_i \times n_h \times n_w ci×nh×nw
- 核 W W W: c i × k h × k w c_i \times k_h \times k_w ci×kh×kw
- 输出 Y Y Y: m h × m w m_h \times m_w mh×mw
Y = ∑ i = 0 c i X i , : , : ★ W i , : , : Y=\sum^{c_i}_{i=0} X_{i,:,:} ★ W_{i,:,:} Y=i=0∑ciXi,:,:★Wi,:,:
注: ★ ★ ★ 表示卷积操作。
2.2 多输出通道
无论有多少输入通道,到目前为止我们只用到单输出通道。
我们可以有多个三位卷积核,每个核生成一个输出通道。
- 输入 X X X: c i × n h × n w c_i \times n_h \times n_w ci×nh×nw
- 核 W W W: c o × c i × k h × k w c_o \times c_i \times k_h \times k_w co×ci×kh×kw
- 输出 Y Y Y: c o × m h × m w c_o \times m_h \times m_w co×mh×mw
Y i , : , : = ∑ i = 0 c i X ★ W i , : , : , : f o r i = 1 , . . . , c o Y_{i,:,:}=\sum^{c_i}_{i=0} X ★ W_{i,:,:,:} \space for \space i=1,..., c_o Yi,:,:=i=0∑ciX★Wi,:,:,: for i=1,...,co
c i c_i ci 为输入通道数, c o c_o co 为输出通道数
2.3 多个输入和输出通道
每个输出通道可以识别特定模式。

输入通道核识别并组合输入图像中的模式。
2.4 1 × 1 1 \times 1 1×1 卷积层
k h = k w = 1 k_h = k_w = 1 kh=kw=1,经常包含在复杂深层网络的设计中。
它不识别空间模式,只是融合通道。

相当于输入形状为 n h n w × c i n_hn_w \times c_i nhnw×ci,权重为 c o × c i c_o \times c_i co×ci 的全连接层。
2.5 2D卷积层(一般情况)
- 输入 X X X: c i × n h × n w c_i \times n_h \times n_w ci×nh×nw
- 核 W W W: c o × c i × k h × k w c_o \times c_i \times k_h \times k_w co×ci×kh×kw
- 偏差 B B B: c o × c i c_o \times c_i co×ci
- 输出 Y Y Y: c o × m h × m w c_o \times m_h \times m_w co×mh×mw
Y = X ★ W + B Y=X ★ W + B Y=X★W+B - 计算复杂度(浮点计算数 FLOP) O ( c i c o k h k w m h m w ) O(c_ic_ok_hk_wm_hm_w ) O(cicokhkwmhmw)

2.6 代码实现
2.6.1 多输入通道
每个通道进行卷积运算,然后再把结果求和。
!pip install -U d2l
import torch
from d2l import torch as d2l
def corr2d_multi_in(X, K):
# 先遍历“X”和“K”的第0个维度(通道维度),再把它们加在一起
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
验证:
X = torch.tensor([[[0.0, 1.0, 2.0],
[3.0, 4.0, 5.0],
[6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0],
[4.0, 5.0, 6.0],
[7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0],
[2.0, 3.0]],
[[1.0, 2.0],
[3.0, 4.0]]])
corr2d_multi_in(X, K)
2.6.2 多输出通道
计算多个通道的输出:
def corr2d_multi_in_out(X, K):
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
K = torch.stack((K, K + 1, K + 2), 0)
K.shape
![]()
torch.stack((K, K + 1, K + 2), 0) 意思是将 (K, K + 1, K + 2) 的结果在 0 0 0 这个维度上堆叠起来。
此时的 K K K:
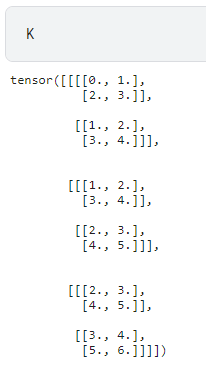
验证:
corr2d_multi_in_out(X, K)
2.6.3 1 × 1 1 \times 1 1×1 卷积
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
c_o = K.shape[0]
X = X.reshape((c_i, h * w))
K = K.reshape((c_o, c_i))
# 全连接层中的矩阵乘法
Y = torch.matmul(K, X)
return Y.reshape((c_o, h, w))
验证:
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
print(Y1, '\n',Y2)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6
2.6.4 Pytorch Conv2d() 参数
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)

注:第一个参数是输入通道数,第二个参数是输出通道数。和李沐老师实现的代码有点区别。
3. 池化层(pooling)
当我们处理图像时,我们希望逐渐降低隐藏表示的空间分辨率、聚集信息,这样随着我们在神经网络中层叠的上升,每个神经元对其敏感的感受野(输入)就越大。
而我们的机器学习任务通常会跟全局图像的问题有关(例如,“图像是否包含一只猫呢?”),所以我们最后一层的神经元应该对整个输入的全局敏感。通过逐渐聚合信息,生成越来越粗糙的映射,最终实现学习全局表示的目标,同时将卷积图层的所有优势保留在中间层。
此外,当检测较底层的特征时(如边缘),我们通常希望这些特征保持某种程度上的平移不变性。例如,如果我们拍摄黑白之间轮廓清晰的图像 X X X,并将整个图像向右移动一个像素,即 Z [ i , j ] = X [ i , j + 1 ] Z[i, j] = X[i, j + 1] Z[i,j]=X[i,j+1],则新图像 Z Z Z 的输出可能大不相同。而在现实中,随着拍摄角度的移动,任何物体几乎不可能发生在同一像素上。即使用三脚架拍摄一个静止的物体,由于快门的移动而引起的相机振动,可能会使所有物体左右移动一个像素(除了高端相机配备了特殊功能来解决这个问题)。
引入池化层的目的:
- 降低卷积层对位置的敏感性
- 降低对空间降采样表示的敏感性
3.1 最大池化层和平均池化层
池化窗口从输入张量的左上角开始,从左往右、从上往下的在输入张量内滑动。在汇聚窗口到达的每个位置,它计算该窗口中输入子张量的最大值或平均值。计算最大值或平均值是取决于使用了最大池化层还是平均池化层。
3.2 填充、步幅和多通道
- 池化层核卷积层类似,都具有填充和步幅
- 没有可学习的参数
- 在每个输入通道应用池化层以获得相应的输出通道
- 输出通道数=输入通道数
池化层之后的特征图形状变化:
⌊ ( n h − k h + p h ) / s h + 1 ⌋ × ⌊ ( n w − k w + p w ) / s w + 1 ⌋ \lfloor (n_h-k_h+p_h)/s_h+1\rfloor \times \lfloor (n_w-k_w+p_w)/s_w+1\rfloor ⌊(nh−kh+ph)/sh+1⌋×⌊(nw−kw+pw)/sw+1⌋
3.3 代码实现
3.3.1 池化层正向传播
# !pip install -U d2l
import torch
from torch import nn
from d2l import torch as d2l
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
# 这里和卷积操作类似
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y
pool_size 为窗口大小。
验证:
X = torch.tensor([[0.0, 1.0, 2.0],
[3.0, 4.0, 5.0],
[6.0, 7.0, 8.0]])
pool2d(X, (2, 2))
pool2d(X, (2, 2), 'avg')
3.3.2 填充和步幅
X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X

设置最大池化窗口为 3 × 3 3 \times 3 3×3:
pool2d = nn.MaxPool2d(3)
pool2d(X)
![]()
注:Pytorch 默认情况下,步幅与池化窗口的大小相同:
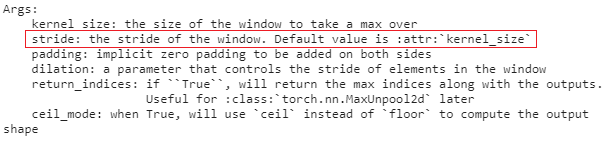
设置填充和步幅:
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)
3.3.3 多通道
池化层在每个输入通道上单独运算:
X = torch.cat((X, X + 1), 1)
X
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
4 Q&A
4.1 池化层为什么目前用的越来越少?
李沐老师的个人理解:
池化层两个主要作用:
- 对卷积的位置没那么敏感
- 减少计算量
一个方面,目前的方法是在卷积层设置一个步幅参数,淡化了池化的作用。另一个方面,一般都会对数据进行数据增强(偏移旋转等操作),也是淡化了池化层的作用。






