论文笔记（二十一）：Fusing Joint Measurements and Visual Features for In-Hand Object Pose Estimation

文章概括

作者：Martin Pfanne，Maxime Chalon，Freek Stulp，and Alin Albu-Sch¨affer
来源：IEEE ROBOTICS AND AUTOMATION LETTERS, VOL. 3, NO. 4, OCTOBER 2018
原文：https://ieeexplore.ieee.org/abstract/document/8405543
代码、数据和视频：
系列文章目录：
上一篇：
论文笔记（二十）VisuoTactile 6D Pose Estimation of an In-Hand Object using Vision and Tactile Sensor Data
下一篇：

摘要

对于一个机器人来说，要完成复杂的操纵任务，如手内操纵，需要随时了解抓取的状态。此外，即使是简单的取放任务也可能失败，因为在抓取过程中物体的意外运动没有被考虑在内。这封信提出了一种方法，通过结合手指测量，即关节位置和扭矩，以及从单眼摄像机图像中提取的视觉特征来估计抓握状态。不同的传感器模式通过扩展的卡尔曼滤波器进行融合。手指测量可以检测到手指和估计物体之间的接触并解决碰撞问题，而视觉特征则用于将物体与摄像机视图对齐。用DLR机器人David进行的实验表明，该方法可以应用于广泛的物体和操纵场景。它们还提供了对不同的补充测量类型的优势和局限性的深入了解。

索引关键词——抓取和操纵的感知、灵巧的操纵、传感器融合。

1. 介绍

受到人手能力的启发，机器人操纵器变得越来越灵巧、顺从和敏感。然而，虽然这些机械手为与环境进行复杂的互动提供了新的可能性，但实际进行熟练的操纵在很大程度上仍然是一个开放的问题。使得可靠地操纵一个物体具有挑战性的一个方面是，它需要在任何时候都了解抓握的状态。事实上，即使是简单的取放任务，也可能因为关于物体在手内的位置的不可靠信息而失败。在抓取时，规划模型或执行过程中的不准确往往会导致物体的移动与预期不同。尽管物体可能仍然以稳定的抓握方式安顿下来，但如果不加以考虑，这些偏差可能对任务的结果产生负面影响。例如，图1中的番茄酱瓶，如果在释放之前没有补偿它在抓取过程中的意外倾斜，就会摔倒。

2. 贡献

我们提出了一个在GPU上并行化的鲁棒性粒子过滤器，它可以在一连串的RGB-D图像上跟踪一个已知的3D物体模型。与PCL跟踪[27]不同的是，我们渲染了三维物体模型，以用于似然性评估，因此我们的方法可以跟踪物体，尽管有明显的姿势变化。我们的主要贡献如下：

• 我们采用扩展特征来评估每个粒子状态的可能性。虽然以前的大部分工作主要依靠二维边缘[13], [14]或强度差异[17], [18]来计算粒子的重要性权重，但我们同时使用RGB-D图像和OpenGL渲染中的光度（颜色）和几何特征（三维点和表面法线）。

• 我们利用OpenGL中的帧缓冲对象扩展（FBO）和CUDA OpenGL互操作性来减少渲染结果到CUDA内存空间的映射时间。正如文献[14]所提到的，OpenGL帧缓冲区和CUDA内存空间之间的映射所花费的时间与将渲染结果复制到CPU内存空间的时间一样多。为了避免这个问题，我们的渲染是在FBO中进行的，所以映射的时间几乎可以忽略不计。

• 我们设计了一种层次化的方法来考虑物体的多种渲染。虽然PCL跟踪[26]只维护一个参考物体云，但我们将物体渲染到具有不同姿势的多个视口。如果我们把所有粒子的姿势都绘制到GPU的渲染缓冲区，那将是最理想的，但由于缓冲区的内存限制，这是不可能的。相反，我们的方法是将物体渲染到V个视口，每个粒子从V个视口中搜索最接近的渲染，这样，每个似然评估都是通过将最接近的渲染结果与当前粒子状态进行转换来进行的（见图2）。

用于似然评估的多次渲染。感兴趣的对象用前五个粒子的状态进行渲染，并根据渲染结果评估这五个粒子的可能性。对于其余的粒子，每个粒子找到最接近的渲染，并使用渲染结果来评估其似然性。左边和右边的图像代表了GPU中的彩色和正常渲染。(最好以彩色观看)

据我们所知，我们提出的解决方案是第一个利用RGB-D传感器的丰富视觉特征进行6-DOF物体姿势跟踪的实时粒子滤波器。图1显示了我们跟踪的一个例子，其中一个目标物体在背景杂波中被跟踪。渲染的三维网格模型代表了粒子的平均值，用于可视化目的。

本文的组织结构如下。第三节简要介绍了用于6-DOF物体姿势跟踪的粒子过滤器，第四节介绍了采用点、颜色和法线的似然函数。在第五节进一步解释了OpenGL和CUDA的实现之后，第六节将我们的方法与合成和真实的RGB-D图像序列中的基线进行了比较。

3. 粒子滤波器

在6-DOF姿态跟踪问题中，采用粒子滤波器对感兴趣的物体随时间变化的轨迹进行采样。在粒子滤波框架中，物体姿势$p({\mathrm{X}}_t|Z_{1:t})$在当前时间t的后验概率密度函数被表示为一组加权粒子，即

$$St=\{({\mathrm{X}}_t^{(1)},{\pi }_t^{(1)}),...,({\mathrm{X}}_t^{(N)},{\pi }_t^{(N)})\}\text{\hspace{1em}(1)}$$

其中，粒子${\mathrm{X}}_t^{(n)}\in SE(3)$代表样本，归一化的重要性权重${\pi }_t^{(n)}$与似然函数$p({\mathrm{Z}}_t|{\mathrm{X}}_t^{(n)})$成正比，$N$是粒子的总数目。在每个时间$t$，粒子过滤器执行顺序重要性抽样与重抽样[10]。当前状态${\mathcal{X}}_t$可以通过加权粒子平均值来估计：

$${\mathcal{X}}_t=\epsilon |S_t|=\sum _{n=1}^N{\pi }_t^{(n)}{\mathrm{X}}_t^{(n)}\text{\hspace{1em}(2)}$$

正如我们在[15]中已经表明的，当我们估计均值时，我们需要得到一个有效的旋转${\mathrm{R}}_t\in SO(3)$，因为算术均值${\bar{\mathrm{R}}}_t=\frac{1}{N}{\sum }_{n=1}^N{\mathrm{R}}_t^{（n）}$通常不在$SO(3)$组。根据[28]，所需的平均旋转可以通过算术平均数的正交投影来计算，为

$${\mathrm{R}}_t=\{\begin{array}{rcl}\mathrm{V}{\mathrm{U}}^T& & \mathrm{when}\det ({\bar{\mathrm{R}}}_t^T)>0\\ \mathrm{VH}{\mathrm{U}}^T& & \mathrm{otherwise},\end{array}\text{\hspace{1em}(3)}$$

其中$\mathrm{U}$和$\mathrm{V}$是通过${\bar{\mathrm{R}}}_{\mathrm{t}}^{\mathrm{T}}$的奇异值分解（即${\bar{\mathrm{R}}}_{\mathrm{t}}^{\mathrm{T}}=\mathrm{U\Sigma }{\mathrm{V}}^{\mathrm{T}}$)和$\mathrm{H}=\mathrm{diag}[1,1,-1]$估计的。

4. 可能性评估

设计一个高效和稳健的似然函数是至关重要的，因为它直接决定了粒子过滤在时间和精度方面的整体性能。当考虑到RGB-D相机时，我们可以采用各种测量方法。三维点坐标、点的颜色、表面法线、曲率、来自深度不连续的边缘或表面纹理等。在这项工作中，我们选择点坐标$\mathrm{x}\in {\mathbb{R}}^3$和它们相关的颜色$\mathrm{c}\in {\mathbb{R}}^3$和法线$\mathrm{n}\in {\mathbb{R}}^3$。因此，一个测量点$\mathrm{p}$被定义为

$$\mathrm{p}=({\mathrm{x}}^{\mathrm{T}},{\mathrm{n}}^{\mathrm{T}},{\mathrm{c}}^{\mathrm{T}}{)}^{\mathrm{T}}\in {\mathbb{R}}^9\text{\hspace{1em}(4)}$$

为了清楚地记述，让我们为$\mathrm{p}$定义访问操作符，以便于

$$\mathrm{x}(\mathrm{p})=({\mathrm{x}}^{\mathrm{T}}1{)}^{\mathrm{T}}\in {\mathbb{R}}^4\text{\hspace{1em}(5)}$$
$$\mathrm{n}(\mathrm{p})=({\mathrm{n}}^{\mathrm{T}}1{)}^{\mathrm{T}}\in {\mathbb{R}}^4\text{\hspace{1em}(6)}$$
$$\mathrm{c}(\mathrm{p})=\mathrm{c}\in {\mathbb{R}}^3\text{\hspace{1em}(7)}$$

我们选择这三种测量方法的原因是，这种组合允许我们在给定的RGB-D场景和计算机图形管道的渲染结果之间进行直接比较。因此，我们可以有效地计算出大量粒子的可能性。

鉴于当前的姿势假设${\mathrm{X}}_{\mathrm{t}}^{(\mathrm{n})}$和渲染的物体模型${\mathrm{M}}_{\mathrm{t}}$，场景${\mathrm{Z}}_{\mathrm{t}}$的可能性被定义为

$$\mathrm{p}({\mathrm{Z}}_{\mathrm{t}}|{\mathrm{X}}_{\mathrm{t}}^{(\mathrm{n})},{\mathrm{M}}_{\mathrm{t}})=\prod _{(i,j)\in \mathcal{A}}\mathrm{p}({\mathrm{z}}_{\mathrm{t}}^{(\mathrm{i})}|{\mathrm{X}}_{\mathrm{t}}^{(\mathrm{n})},{\mathrm{m}}_{\mathrm{t}}^{(\mathrm{j})})\text{\hspace{1em}(8)}$$

其中$\mathcal{A}=\{(i,j)|proj(\mathrm{x}({\mathrm{z}}_{\mathrm{t}}^{(\mathrm{i})}))=\mathrm{proj}({\mathrm{X}}_{\mathrm{t}}^{(\mathrm{n})}\cdot \mathrm{x}({\mathrm{m}}_{\mathrm{t}}^{(\mathrm{j})}))\}$是场景$Z_t$和物体模型$M_t$之间的点关联集合，$z_t^{(i)},m_t^{(j)}\in {\mathbb{R}}^9$分别是场景和模型中的对应点。运算符$\mathrm{proj}(\cdot )$通过用已知的相机固有参数$\mathrm{K}\in {\mathbb{R}}^{3\times 3}$对点进行投影，计算给定的三维同质点坐标的二维图像坐标。利用$\mathrm{proj}$算子，可以有效地确定点的关联$\mathcal{A}$。然后，每个关联$(i，j)$的可能性被定义为

$$\begin{array}{rl}p(z_t^{(i)}|{\mathrm{X}}_t^{(n)},{\mathrm{m}}_t^{(j)})=& ex{p}^{-{\lambda }_e\cdot d_e(x(z_t^{(i)}),X_t^{(n)}\cdot x(m_t^{(j)}))}\\ \cdot & ex{p}^{-{\lambda }_n\cdot d_n(n(z_t^{(i)}),X_t^{(n)}\cdot n(m_t^{(j)}))}\\ \cdot & ex{p}^{-{\lambda }_c\cdot d_c(c(z_t^{(i)}),c(m_t^{(j)}))}\end{array}\text{\hspace{1em}(9)}$$

其中$d_e({\mathrm{x}}_1,{\mathrm{x}}_2)$, $d_n({\mathrm{n}}_1,{\mathrm{n}}_2)$, 和 $d_c({\mathrm{c}}_1,{\mathrm{c}}_2)$是欧氏距离、法线距离和颜色距离，如下所示

$$d_e({\mathrm{x}}_1,{\mathrm{x}}_2)=\{\begin{array}{rcl}& ||{\mathrm{x}}_1-{\mathrm{x}}_2||& \mathrm{if}||{\mathrm{x}}_1-{\mathrm{x}}_2||\le \tau \\ & 1& \mathrm{otherwise},\end{array}\text{\hspace{1em}(10)}$$

$$d_n({\mathrm{n}}_1,{\mathrm{n}}_2)=\frac{\mathrm{co}{\mathrm{s}}^{-1}({\mathrm{n}}_1^{\mathrm{T}}{\mathrm{n}}_2-1)}{\pi }\text{\hspace{1em}(11)}$$

$$d_c({\mathrm{c}}_1,{\mathrm{c}}_2)=||{\mathrm{c}}_1-{\mathrm{c}}_2||\text{\hspace{1em}(12)}$$

并且${\lambda }_e,{\lambda }_n,{\lambda }_c$是决定距离对似然的敏感性的参数。(10)中的$\tau$是两点间欧氏距离的阈值。注意（11）中的${\mathrm{n}}_1,{\mathrm{n}}_2\in {\mathbb{R}}^4$是同质的点坐标，所以需要从内积中减去1。对于（12）中的颜色距离，只要$0\le d_c(c_1,c_2)\le 1$，任何种类的颜色空间都可以考虑，但我们采用HSV颜色空间，主要是因为它对光照变化的不变性。请注意，物体模型点$m_t^{(j)}$的点和法线坐标是在物体坐标框架内的，所以应该考虑由当前姿势${\mathrm{X}}_t^{(n)}$变换的点来计算距离。

5. 实施细节

正如我们在第二节中已经提到的，我们在渲染缓冲区中用前五个粒子的姿势将我们感兴趣的物体渲染到五个视口上。对于其余的粒子，每个粒子都会找到一个与姿势假设最接近的渲染结果，并将最近的渲染结果与当前的姿势进行转换。对于这个计算，我们需要访问渲染结果中所有可见点的颜色、顶点（即三维点）和法线信息。通过访问渲染缓冲区来获得颜色信息是比较直接的，但是从缓冲区访问三维点和三维法线数据就比较麻烦了。为了解决这个问题，我们采用OpenGL着色语言（GLSL）来直接访问图形管道中间的点和法线数据。对于点的信息，我们设计了一套简单的顶点和片段着色器，使可见点的三维坐标gl_Vertex被保存为彩色纹理点gl_FragColor。同样地，对于法线数据，我们使用了另一套顶点和片段着色器，这样物体的表面法线gl_Normal就被保存在彩色纹理点中。请注意，这些点和法线是在物体坐标帧中的，所以我们不需要在渲染结果上进行反变换，然后再相对于当前粒子的姿势进行变换。

多视口渲染的主要目的不是为了可视化，而是为了对每个粒子进行可能性评估。因此，对于我们的渲染目的来说，使用Frame Butter Object（FBO，GL_ARB_framebuffer_object）是一个不错的选择。FBO是OpenGL对屏幕外帧缓冲器的扩展。与窗口系统提供的OpenGL默认的帧缓冲区不同，FBO更加灵活和高效，因为所有绑定在FBO中的资源都在同一个上下文中共享。FBO允许用户将多个纹理图像附加到颜色附件中。为了我们的目的，我们将三个纹理图像附加到三个颜色附件中。GL_COLOR_ATTACHMENT0用于颜色数据，GL_COLOR_ATTACHMENT1用于点数据，GL_COLOR_ATTACHMENT2用于正常数据。在渲染阶段，我们感兴趣的对象被绘制到每个颜色附件上。虽然颜色纹理是用通常的OpenGL渲染方式绘制的，但点和法线纹理是通过上述着色器程序渲染的。对于每一次渲染，对象都是通过调用glViewport()渲染到V视口。

用着色器程序渲染物体后，我们在GPU上评估似然函数。为了在我们的可能性评估内核中利用附在FBO上的纹理图像，我们使用了CUDA的OpenGL互操作性，允许将OpenGL缓冲区映射/解映射到CUDA的内存空间。因此我们的CUDA内核可以非常有效地访问渲染的缓冲区。

6. 实验

在本节中，我们提出了一组PCL跟踪和我们提出的方法之间的比较实验。在第VI-B节中，我们使用一组具有地面真实物体轨迹的合成RGB-D序列对这两种方法的性能进行了定量评估，然后在第VI-C节中使用真实的RGB-D序列进行了定性评估。在评估中，两个跟踪器都是以合成序列中的已知地面实况和从足够接近的初始姿态开始运行我们的跟踪器后的收敛姿态估计值作为初始化。PCL跟踪提供了一个基于[30]的自适应颗粒大小的选项，但在这里，为了与我们的方法进行公平的比较，以及对不同颗粒大小的性能评估，我们考虑了固定的颗粒大小。所有的实验都是使用一台标准的台式电脑（英特尔Core2 Quad CPU Q9300，8G内存）和一个现成的GPU（NVIDIA GeForce GTX 590，CUDA 4.1）以及一个RGB-D相机（华硕Xtion Pro Live）进行的。

A. 物体模型

在实验中，我们选择了四个物体，并通过使用RGB-D传感器生成物体的3D网格模型（图3）。为了生成网状模型，我们首先获得多个RGB-D视图并注册。我们可以使用RGB-D SLAM方法之一[23], [24], [31]来注册多个视图，但为了简单起见，我们采用了几个ARTags。一旦多个视图被融合，物体云就被从背景云中分割出来，并通过泊松重建算法[29]重建成一个网状模型。由于PCL跟踪不能使用三维网格模型，通过渲染初始姿势得到的物体点云被送入作为参考模型。

图3. 物体和厨房的网格模型。物体模型是通过融合多个RGB-D视图生成的，然后运行Poisson重建算法[29]。为了生成一组合成序列，从谷歌3D仓库下载了一个厨房模型。从左到右，"潮汐"、"牛奶"、"橙汁"、"Kinect盒子 "和 "厨房"。

B. 合成序列

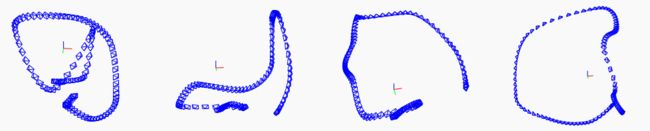
为了进行定量分析，我们生成了一组合成的RGB-D序列。为了模拟一个真实的环境，我们从谷歌3D仓库下载了一个虚拟厨房模型（见图3）。将每个物体模型放在厨房模型中后，通过在物体周围移动虚拟摄像机来生成一组合成序列。图4显示了合成数据的摄像机轨迹，这些轨迹在摄像机的平移、旋转和速度方面表现出高度的变化。物体的轨迹被保存下来，作为物体相对于摄像机坐标框架的地面真实姿态。

图4. 合成序列中的相机轨迹。合成的RGB-D序列是用其对应的物体的地面真实轨迹生成的。请注意平移、旋转和速度方面的明显变化。从左到右是 "潮汐"、"牛奶"、"橙汁 "和 "Kinect盒子 "的轨迹。

为了比较我们的方法和PCL跟踪，我们计算了四种合成RGB-D序列的均方根（RMS）误差和每帧的平均计算时间，如表I所示。为了便于比较，更好的结果用粗体字表示。RMS误差因物体类型和序列的难度而不同。但总的趋势是，随着粒子数N的增加，平移和旋转误差会减少。以 "潮汐 "序列为例，它与其他序列相比相当简单，当N≤800时，PCL跟踪报告的结果略好。但随着N的增加，我们的跟踪器显示出更准确的结果。在 "潮汐 "序列中，一个有趣的事实是，PCL跟踪在Z方向的翻译中显示出稍好的结果。这可能是由于PCL跟踪只有一个参考物体点云作为物体模型，所以它确实在这个方向上导致了较小的误差。然而，当它在更具挑战性的序列上运行时，有限的参考云的数量就会出现问题。请注意，“牛奶”、"橙汁 "和 "Kinect盒子 "序列中的平移和旋转都有很大的误差。由于物体本身是自对称的，每个物体的一个参考视图不足以跟踪整个序列中的物体。如图5和图6所示，在追踪过程中，PCL追踪经常陷入局部最小值，而我们的方法可以稳健地追踪序列中的物体。

图5. 对 "橙汁 "和 "Kinect盒子 "合成序列的跟踪结果。对于这两个序列，上面几行显示的是我们的方法的跟踪结果，而下面几行显示的是PCL跟踪的结果（"橙汁 "序列的N=6400，"Kinect盒子 "序列的N=12800）。在这两个序列中，我们的方法都能很好地跟踪真实的物体轨迹，但由于物体模型的限制，PCL跟踪往往会丢失。(最好以彩色观看)

图6. 图5中 "Kinect Box "结果的6-DOF姿势图。虽然我们的方法很好地遵循了地面实况，但由于物体模型的限制，PCL跟踪存在着错误的跟踪。

对于机器人应用，计算时间确实很重要，因为它直接决定了机器人系统的性能和可靠性。正如我们在表一和图8中看到的，两种方法的计算时间都随着N的增加而线性增加。然而，我们的跟踪每帧只需要大约50毫秒（即每秒20帧），有几千个粒子，而PCL跟踪则受到低帧率的影响。尽管PCL跟踪在 "潮汐 "序列中表现出相当的性能，但如果我们考虑到真实的帧速率，PCL跟踪会因为丢失的帧而产生更多的误差。

表一

图8. Boxplots显示了我们在 "潮汐 "合成序列上的跟踪（左）和PCL跟踪（右）的计算时间。对于这两种方法，时间随着粒子数N的增加而线性增加，但我们的增加率要小得多。请注意，在N≤3200之前，我们方法的计算时间小于50毫秒。

C. 真实序列

我们在一组真实的图像序列中运行这两种跟踪方法，与合成序列相比，真实的图像序列表现出明显的噪声和更多的物体运动变化。图7显示了对 "潮汐 "和 "牛奶 "序列的姿势跟踪结果。为了清晰的可视化，来自RGB-D序列的RGB通道被转换为灰度，每个渲染的物体模型被画在它们上面。无效的深度点（也被称为南点）被显示为黑点。对于这两个序列，都采用了N = 1600粒子。由于物体的旋转变化很大，PCL跟踪（每个序列中的下行）经常失去跟踪。由于采用了三维物体模型并在多个视图中进行渲染，我们的跟踪能够可靠地跟踪物体，尽管有挑战性的旋转运动。

7. 结论

我们提出了一种基于GPU上的粒子过滤器的RGB-D物体跟踪方法。丰富的视觉特征被用来评估每个粒子的可能性，这个过程是大多数粒子过滤器的典型瓶颈，在GPU上被并行化，因此我们提出的解决方案实现了实时性能。通过对合成和真实的RGB-D序列进行广泛的实验，我们验证了我们的方法不仅更快，而且比PCL跟踪更准确。

8. 鸣谢

这项工作得到了波音公司的部分赞助。在此对这种支持表示感谢。