dijkstra算法C++实现

1 acwing模板

1.1 稠密图-用邻接矩阵

//dijkstra()   迪杰斯特拉算法
//输入
const int N = 510;
int dist[N];//dist[i]表示结点i到起点的距离
int g[N][N];//g[i][j]表示结点i到结点j的边的长度，稠密图用邻接矩阵来存储
bool st[N];//st[i]表示该结点是否确定了最小距离，1是确定，0是未确定
int n, m;//n个点，m条边
//输出
dist[];//每个结点到起点的最短距离
//适用情况
边权非负
第1步：初始化dist数组为正无穷，起点距离dist[1]为0
memset(d, 0x3f, sizeof d);
d[1] = 0;
第2步：循环n次
第2.1步：找到某个结点，它属于没有确定最短路的点集，它距离起点最近
int t = -1;
for(int i = 1; i <= n; i++)
	if(st[i] == 0 && (t == -1 || dist[t] > dist[i]))
		t = i;
第2.2步：设置st[t] = 1，用这个结点的dist去更新剩余结点的dist
st[t] = 1;
for(int i = 1; i <= n; i++)
	if(st[i] == 0)
		dist[i] = min(dist[i], dist[t] + g[t][i]);
结束！

示例代码如下，

#include 
#include 
#include 

using namespace std;

const int N = 510;
int dist[N];//dist[i]表示结点i到起点的距离
int g[N][N];//g[i][j]表示结点i到结点j的边的长度
bool st[N];//st[i]表示该结点是否确定了最小距离，1是确定，0是未确定
int n, m;


void dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//把距离初始化为正无穷
    dist[1] = 0;
    
    int iter = n;
    while(iter--)//n个点，循环n次
    {
        int t = -1;
        //t随便初始化了一个不存在的结点，它最终用来存储未确定最小距离的结点，且该结点与其它结点相比目前到起点的距离最小
        for(int i = 1; i <= n; i++)
            if(st[i] == 0 && (t == -1 || dist[t] > dist[i]))
                t = i;
                
        st[t] = true;
        //用结点t依次取更新其它结点到起点的距离，dist[i] = min(dist[i], dist[t] + g[t][i]);
        for(int i = 1; i <= n; i++)
            if(st[i] == 0)
                dist[i] = min(dist[i], dist[t] + g[t][i]);
                
    }
    
}

int main()
{
    
    cin >> n >> m;
    
    memset(g, 0x3f, sizeof g);//将边先初始化为正无穷
    
    while(m--)
    {
        int x, y, z;
        cin >> x >> y >> z;
        g[x][y] = min(g[x][y], z);//存在重边
        //对于自环，不做处理，它不影响结果的计算
    }
    
    
    dijkstra();
    
    
    if(dist[n] == 0x3f3f3f3f)
        cout << "-1" << endl;
    else
        cout << dist[n] << endl;
    

    return 0;
}

输入为，

3 3
1 2 2
2 3 1
1 3 4

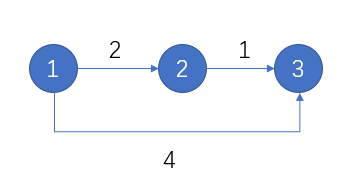
用图表示为，

输出为起点到终点的最短距离，

3

1.2 稀疏图-用邻接表

//dijkstra()算法
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int head[N];
int dist[N];
bool st[N];
int e[N], ne[N], w[N], idx;
//head,dist和st用来存图结点，e,ne,和w用来存边
第1步：初始化
memset(head, -1, sizeof head);//邻接表初始化
memset(dist, 0x3f, sizeof dist);//dist初始化
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});//first存距离，second存图结点
第2步：遍历图
第2.1步：取出当前距离最小的结点
PII t = heap.top();
heap.pop();
int ver = t.second, d = t.first;
第2.2步：已知a->b中，结点a的距离d，用它去更新b
for(int i = head[ver]; i != -1; i = ne[i])
{
	int j = e[i];
	if(dist[j] > d + w[i])
	{
		dist[j] = d + w[i];
		heap.push({dist[j], j});
	}
}
结束！

示例代码为，

#include 
#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 1.5e5 + 10;
int st[N];
int head[N];
int dist[N];
int e[N], ne[N], w[N], idx;//用来存边
int n, m;

//边:a->b,权重为c
void add(int a, int b, int c)
{
    e[idx] = b;
    ne[idx] = head[a];
    w[idx] = c;
    head[a] = idx;
    idx++;
    
}


void dijkstra()
{
    //图的遍历
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});//first表示距离，second表示结点
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    while(heap.size())
    {
        PII t = heap.top();
        heap.pop();
        
        int ver = t.second, d = t.first;
        if(st[ver] == 1) continue;
        st[ver] = 1;
        
        //a->b, 已知a的距离和边权，去更新b的距离
        for(int i = head[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > d + w[i])
            {
                dist[j] = d + w[i];
                heap.push({dist[j], j});
            }
        }    
    }
}

int main()
{
    
    cin >> n >> m;//n个结点, m条边
    
    memset(head, -1, sizeof head);
    
    while(m--)
    {
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z);
    }
    
    dijkstra();
    
    if(dist[n] == 0x3f3f3f3f)
        cout << -1 << endl;
    else
        cout << dist[n] << endl;
        
    
    return 0;
}

示例输入，

3 3
1 2 2
2 3 1
1 3 4

示例输出，

3

2 leetcode模板

743.网络延迟时间

class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        const int inf = INT_MAX / 2;
        vector<vector<pair<int,int>>> g(n);
        for (auto &t : times) {
            int x = t[0] - 1, y = t[1] - 1;
            g[x].emplace_back(y, t[2]);
        }

        vector<int> dist(n, inf);
        dist[k - 1] = 0;
        priority_queue<pair<int, int>, vector<pair<int,int>>, greater<>> q;
        q.emplace(0, k - 1);
        while (!q.empty()) {
            auto p = q.top();
            q.pop();
            int time = p.first, x = p.second;
            if (dist[x] < time) {
                continue;
            }
            for (auto &e : g[x]) {
                int y = e.first, d = dist[x] + e.second;
                if (d < dist[y]) {
                    dist[y] = d;
                    q.emplace(d, y);
                }
            }
        }

        int ans = *max_element(dist.begin(), dist.end());
        return ans == inf ? -1 : ans;
    }
};