SSD算法简单介绍

SSD算法

论文连接SSD: Single Shot MultiBox Detector

SSD，全称Single Shot MultiBox Detector，是目前主要的检测框架之一，其基于将detection转化为regression的思路，可以一次完成目标定位与分类。该算法基于Faster RCNN中的Anchor，提出了相似的Prior box；该算法修改了传统的VGG16网络：将VGG16的FC6和FC7层转化为卷积层，如图1上的Conv6和Conv7；去掉所有的Dropout层和FC8层；添加了Atrous算法（hole算法），将Pool5从2x2-S2变换到3x3-S1，同时加入基于特征金字塔（Pyramidal Feature Hierarchy）的检测方式，即在不同感受野的feature map上预测目标。

SSD算法工作流程

1. 输入一幅图片，将其输入到预训练好的分类网络中来获得不同大小的特征映射；
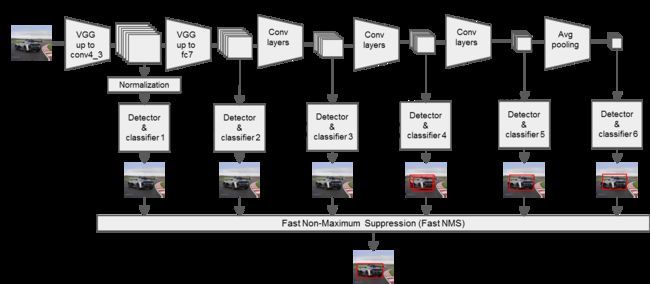
2. 抽取Conv4_3、Conv7、Conv8_2、Conv9_2、Conv10_2、Conv11_2层的feature map，然后分别在这些feature map层上面的每一个点构造6个不同尺度大小的BB（bounding box），然后分别进行检测和分类，生成多个BB，如图1所示；
3. 将不同feature map获得的BB结合起来，经过NMS（非极大值抑制）方法来抑制掉一部分重叠或者不正确的BB，生成最终的BB集合（即检测结果）。
   下图为SSD算法的工作流程图：
   

Defalut box生成规则

为提高目标的识别准确度，该网络预设了多种尺度的目标检测框（Defalut box），每个目标检测框获得的feature map通过softmax分类+bounding box regression获得真实目标的位置。Defalut box是以feature map上每个点的中点为中心（offset=0.5），生成一系列同心的Defalut box（然后中心点的坐标会乘以step，相当于从feature map位置映射回原图位置），使用m(SSD300中m=6)个不同大小的feature map 来做预测，最底层的 feature map 的 scale 值为 Smin=0.2，最高层的为Smax=0.95，其他层通过下面的公式计算得到：
$$s_k=s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1)$$

LOSS计算

SSD算法的目标函数分为两部分：计算相应的default box与目标类别的confidence loss以及相应的位置回归(location loss)。总体loss计算为：
$$L(x,c,l,g)=\frac{1}{N}(L_{conf}(x,c)+\alpha L_{loc}(x,l,g))$$
其中N是match到Ground Truth的default box数量；而α参数用于调整confidence loss和location loss之间的比例，默认α=1；
位置回归则是采用 Smooth L1 loss计算预测框box（l）和真值框box（g）直接的loss，其函数表示为:
$$L_{loc}(x,l,g)=\sum _{\in Pos}^N\sum _{m\in cx,cy,w,h}{x}_{ij}^k{smooth}_{L1}(l_i^m-{\hat{g}}_j^m)$$
$${\hat{g}}_j^{c}x=(g_j^{c}y-d_i^{c}y)/d_i^h$$
$${\hat{g}}_j^w=log((g_j^w)/(d_i^w))$$
$${\hat{g}}_j^h=log((g_j^h)/(d_i^h))$$
其中i为预测框序号，j为真值框序号，（cx,cy）是default box（d）的中心坐标，w，h分别是default box（d）的宽和高。
计算相应的default box与目标类别的Confidence loss是：
$$L_{conf}(x,c)=-\sum _{i\in Pos}^N{x}_{ij}^{p}log({\hat{c}}_i^p)-\sum _{i\in Neg}log{\hat{c}}_i^0$$
其中 ${\hat{c}}_i^p=\frac{e^{c_i^p}}{{\sum }_p{e}^{c_i^p}}$ 。$c_i^p$是分类器前级输出单元的输出，$i$表示类别索引，总得类别个数为$p$，${\hat{c}}_i^p$表示的是当前元素的指数与所有元素指数和的比值。

极大值抑制（NMS）筛选

将所有生成的default boxes全部用NMS（极大值抑制）进行筛选，得到最终的目标区域；
$$f(x)=\{\begin{array}{lcl}{S}_i& & iou(M,b_i)<N_t\\ S_{i(1-iou(M,b_i))}& & iou(M,b_i)<N_t\end{array}$$

其中$N_t$是NMS的阈值，$b_i$是检测的bounding box，$s_i$是对应$b_i$框的置信度，$M$是所有检测框的并集。