SSD算法

SSD算法

学习目标

• 知道SSD的多尺度特征图的网络
• 知道SSD中先验框的生成方式
• 知道SSD的损失函数的设计

目标检测算法主要分为两类：

• Two-stage方法：如R-CNN系列算法，主要思路就是通过Selective Search或者CNN网络产生一系列的稀疏矩阵的候选区域，然后对这些候选区域进行分类和回归，two-stage的方法优势在于准确率度高；
• One-stage方法：如YOLO系列方法，主要思路就是均匀地在图片上不同位置进行密集采样，采样时使用不同尺度和长宽比box，然后利用CNN提取特征后直接进行分类和回归，整个过程只需要一步，所以优势在于速度快。我们接下来介绍的SSD方法也是单阶段的算法。

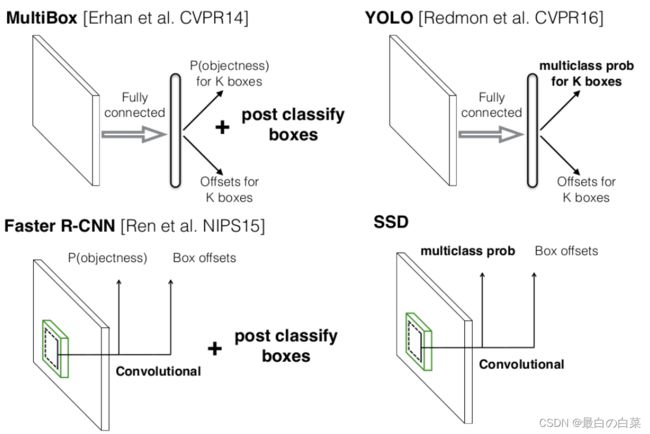
SSD算法的全名是Single Shot MultiBox Detector，Single shot指明了SSD算法属于one-stage方法，MultiBox指明了SSD是多框预测。对于Faster R-CNN，先通过CNN得到候选框，然后进行分类和回归，而YOLO和SSD可以一步完成检测，SSD的特点是：

• SSD提取了不同尺度的特征图来做检测，大尺度特征图可以用来检测小物体，而小特征图用来检测大物体；
• SSD采用了不同尺度和长宽比的先验框，在faster r-cnn和yoloV2,V3中称为Anchors。

SSD网络结构

SSD是YOLO V1出来后，YOLO V2出来前的一款One-stage目标检测器。SSD用到了多尺度的特征图，在之后的YOLO V3的darknet53中，也是用到了多尺度特征图的思想。较浅层的特征图上，每个cell的感受野不是很大，所以适合检测较小的物体，而在较深的特征图上，每个cell的感受野就比较大了，适合检测较大的物体。

SSD采用VGG16作为基础模型，然后在VGG16的基础上新增了卷积层来获得更多的特征图以用于检测。如下图所示：

整个特征图分为三部分：

• backbone: VGGnet用于图片特征提取的网络
• Extra: 用于引出多尺度特征图的网络
• Loc和cls: 用于框位置回归和目标分类的网络

backbone

网络采用VGG16作为基础模型，使用imagenet数据进行预训练后，将conv4-1前一层的maxpooling中池化模式padding改为same(图中对应pytorch中的ceil_mode),使得输出为38x38，Conv4-3就是多尺度特征中的第一个38x38的特征图，因为该层比较靠前，所以在其后面增加了一个L2 Normalization层，对每个像素点在channle维度做归一化。VGG16最后的两个全连接层转换成 3x3 卷积层 conv6和 卷积层conv7，同时将最后的池化层由原来的stride=2的 2x2 变成stride=1的 3x3的池化层。

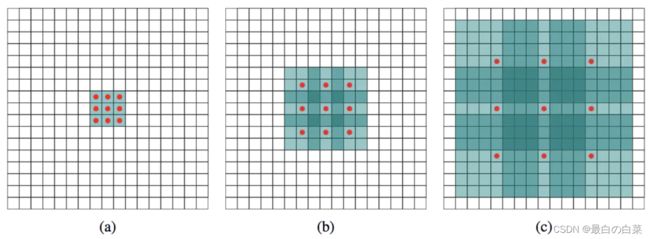
其中conv6使用的Dilated Convolutions，可以翻译为扩张卷积或空洞卷积。与普通的卷积相比，增加了一个扩张率(dilation rate)参数，主要用来表示扩张的大小。扩张卷积与普通卷积的相同点在于，卷积核的大小是一样的，在神经网络中参数数量不变，区别在于扩张卷积具有更大的感受野。如下图所示：

(a) 普通卷积，1-dilated convolution，卷积核的感受野为3×3=93×3=9。 (b) 扩张卷积，2-dilated convolution，卷积核的感受野为7×7=497×7=49。 © 扩张卷积，4-dilated convolution，卷积核的感受野为15×15=22515×15=225。

扩张卷积的感受野的计算方法是：

在tensorflow中实现使用的是：(与普通卷积不同的是指定dilation_rate即可)

layers.Conv2D(1024, 3, padding='same',dilation_rate=6, activation='relu'),

从上图中可以看出，卷积核的参数个数保持不变，感受野的大小随着“dilation rate”参数的增加呈指数增长。

extra部分

为了进行后续的多尺度特征提取，在Backbone后面添加了卷积网络，如下图所示：

新增的Conv8_2，Conv9_2，Conv10_2，Conv11_2提取用于检测的特征图，特征图的大小如下表所示：

红框中的内容是进行多尺度分析的特征图，在加上backbone部分的Conv4_3和Conv7获取的特征图，共提取了6个特征图，其大小分别是 (38, 38), (19, 19), (10, 10), (5, 5), (3, 3), (1, 1)，我们将其送入到loc和cls中进行目标检测。

loc和cls

在backbone和 Extras 在提取的6个特征图的基础上，进行位置信息和分类信息的提取，其结构如下图所示：

该部分主要有3个支路构成，

• PriorBox层，用来生成先验框，也就是在fasterRCNN中的anchorbox，假设先验框种类有3个（一个单元上有3个先验框），一共产生5x5x3=75个先验框
• Localization: 采用一次3×3卷积来进行完成，每个先验框有四个坐标，共有5x5x3x4个预测结果
• 类别置信度confdence：采用一次3×3卷积来进行完成，每个先验框有21个类别预测结果（VOC数据集），共有5x5x3x21个预测结果

整个过程如下图所示：

PriorBox层先验框的生成方法

在这里我们着重介绍PriorBox层先验框的生成方法：

SSD一共有6个不同尺度的特征图，每个特征图上设置的先验框数量不同的（同一个特征图上每个单元设置的先验框是相同的，这里的数目指的是一个单元的先验框数目）。

先验框的设置：包括尺度（或者说大小）和长宽比两个方面。

• 先验框的尺度

先验框的尺度遵守一个线性递增规则：随着特征图大小降低，先验框尺度线性增加，每个先验框的尺度有下式决定：

$s_k=s_{\min }+\frac{s_{\max }-s_{\mathrm{mi}}}{m-1}(k-1),k\in [1,m]$

其中：

m 指的特征图个数，这里设为5 ，因为第一层（Conv4_3层）是单独设置的。sk表示先验框大小相对于图片的比例，而 smin 和 smax表示比例的最小值与最大值，取值为0.2和0.9。

1、对于第一个特征图，其先验框的尺度比例一般设置为 smin/2=0.1 ，尺度为 300×0.1=30。

2、对于后面的特征图，先验框尺度按照 sk 线性增加，增长步长为:

$\lfloor \frac{\lfloor s_{\max }\rfloor -\lfloor s_{\min }\rfloor }{m-1}\rfloor =0.17$

3、根据上式，我们可以计算出各个尺度 sk 的取值为0.20, 0.37,0. 54, 0.71, 0.88

4、然后再乘以原图的大小300，再综合第一个特征图的先验框尺寸，则可得各个特征图的先验框尺寸为30,60,111, 162,213,264。

• 先验框的长宽比

一般选取 ar∈1,2,3,12,13，对于特定的长宽比，按如下公式计算先验框的宽度与高度（后面的 sk均指的是先验框实际尺度，而不是尺度比例）:

$w_k^a=s_k\sqrt{a_r},h_k^a=s_k/\sqrt{a_r}$

默认情况下，每个特征图会有一个 ar=1且尺度为 sk 的先验框，除此之外，还会设置一个尺度为 $s_k^{\prime }=\sqrt{s_k{s}_{k+1}}$且 ar=1的先验框，这样每个特征图都设置了两个长宽比为1但大小不同的正方形先验框。

因此，每个特征图一共有 6 个先验框$1,2,3,\frac{1}{2},\frac{1}{3},1^{\prime }$，但是在实现时，Conv4_3，Conv10_2和Conv11_2层仅使用4个先验框，它们不使用长宽比为$3,\frac{1}{3}$ 的先验框。

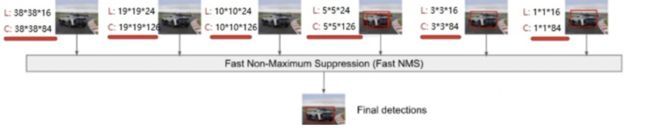
令 nknk为该特征图所采用的先验框数目，那么类别置信度需要的卷积核数量为 nk，而边界框位置需要的卷积核数量为 nk×4。由于每个先验框都会预测一个边界框，

所以SSD一共可以预测 38×38×4+19×19×6+10×10×6+5×5×6+3×3×4+1×1×4=8732个边界框，对于一个300x300的图像就有8732个预测结果，是非常的多的，所以说SSD本质上是密集采样。

loc的预测结果

网络预测输出的边界框与真实的边界框之间存在转换关系，具体如下：

• 先验框位置：

$l=\left(l^{cx},l^{cy},l^w,l^h\right)$

• 真实框的位置：

$p=\left(p^{cx},p^{cy},p^w,p^h\right)$

那么网络输出结果d与边界框的位置存在关系：

$\begin{array}{l}{p}^{cx}=l^w{d}^{cx}+l^{cx},p^{cy}=l^y{d}^{cy}+l^{cy}\\ p^w=l^w\exp \left(d^w\right),p^h=l^h\exp \left(d^h\right)\end{array}$

模型训练

正负样本标记

在训练过程中，首先需要确定训练图片中的 ground truth 与哪一个先验框来进行匹配，与之匹配的先验框所对应的边界框将负责预测它。

SSD的先验框和ground truth匹配原则：

• 正样本

1、对于图片中的每个gt，找到与其IOU最大的先验框，该先验框与其匹配，这样可以保证每个gt一定与某个先验框匹配。

2、对于剩余未匹配的先验框，若某个gt的IOU大于某个阈值(一般0.5)，那么该先验框与这个gt匹配

• 负样本

其它的先验框标记为负样本

注意：

1、某个gt可以和多个先验框匹配，而每个先验框只能和一个gt进行匹配

2、如果多个gt和某一个先验框的IOU均大于阈值，那么先验框只与IOU最大的那个进行匹配

损失函数

SSD的损失函数是位置损失（ loc）与类别置信度损失（conf）的加权和：

$L(x,c,l,g)=\frac{1}{N}\left(L_{\text{conf }}(x,c)+\alpha L_{\text{loc }}(x,l,g)\right)$

其中N是先验框的正样本数量，c为类别置信度预测值， l为先验框的所对应边界框的位置预测值，而 g是ground truth的位置参数，权重系数 α 设置为1。

1. 位置损失函数：

针对所有的正样本，采用 Smooth L1 Loss损失

2. 分类损失函数

对于分类损失，与fasterRCNN一样采用交叉熵损失。

困难样本挖掘

困难样本挖掘的思想是使用网络对样本进行处理，把其中预测错误的负样本(hard negative)放入负样本集合再继续训练网络模型。

在SSD中处理方式是：

• 使用1：3的正负样本比例训练网络，
• 对输入的预测结果按照类别置信度进行降序排序，取出前k个负样本
• 将这k个负样本加入下次迭代的负样本中对网络进行训练。

模型预测

预测过程比较简单，

主要步骤如下：

• 对于每个预测框，首先根据类别置信度确定其类别（置信度最大者）与置信度值，并过滤掉属于背景的预测框。
• 然后根据置信度阈值（如0.5）过滤掉阈值较低的预测框。
• 对于留下的预测框进行解码，根据先验框得到其真实的位置参数（解码后一般还需要做clip，防止预测框位置超出图片）。
• 解码之后，一般需要根据置信度进行降序排列，然后仅保留top-k（如400）个预测框。
• 进行NMS算法，过滤掉那些重叠度较大的预测框。
• 最后剩余的预测框就是检测结果了。

总结

• 知道SSD的多尺度特征图的网络

SSD提取了6个不同特征图进行目标检测

• 知道SSD中先验框的生成方式

SSD在不同尺度的特征图上生成的先验框的尺度和长宽比是不一样的

• 知道SSD的损失函数的设计

分类和回归损失函数的加权和