【Datawhale学习笔记】Pytorch整体框架搭建入门——MNIST时装分类01

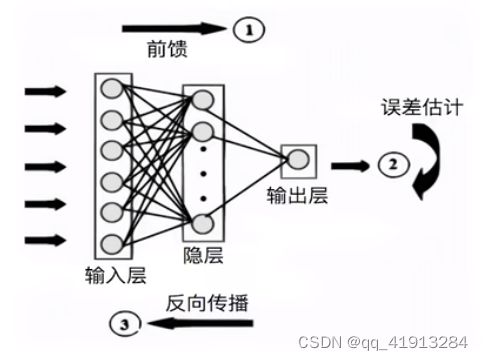
        神经网络的学习主要包含了以下几个过程：
        1.数据预处理

        2.模型的设计

        3.损失函数以及优化方案设计

        4.前向传播

        5.反向传播

        6.更新参数

        上述6点在我看来，前3点是体现了神经网络的设计艺术的——如果把神经网络的学习看作是人和机器的合作，那么前3点工作无疑是需要人工去完成的。在利用Pytorch编写神经网络代码时，前三点往往比较让我头大，特别是第一点！简直像是变形金刚一样，对着数据各种操作，最终把他们变成符合输入条件的样式。

        在不了解神经网络工作原理的情况下，它就像一个黑盒子，输入样本数据，输出预测结果。如果觉得神经网络训练地还不够好，你要做的就是像一个严格的教练一样：惩罚神经网络，让神经网络修改参数，直到满足你的要求（一个教练自己不一定是好运动员，但一定懂得监控）。一个神经网络中可能有大量（上百万）参数，如何修改每一个参数的数值呢？这就要求从结果出发（损失函数），向前回溯（对每一层的变量求导），采用梯度下降的方法来更新参数，这就是所谓的backprop反向传播。

        上面的过程，在Pytorch中早就封装好了，只需要几行命令就可以完成——只要挑选合适的损失函数、设置优化方法，基本上是“傻瓜式”操作。

        接下来就看看Pytorch能不能完成MNIST时装分类任务吧！

        第0步：召唤package&配置训练环境&设置超参数

import os
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim
from torch.utils.data import Dataset,DataLoader

        因为我也是初学Pytorch，买不起GPU，这里我用的是CPU

device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

        超参数设置：

batch_size = 256
num_workers = 4
lr = 1e-4
epoch = 20

        第1步：数据预处理

        数据集FashionMNIST可以从Kaggle中下载（虽然Pytorch中也自带了这一数据集，但为了熟练掌握数据处理的过程，从网上下载数据集、把数据集转化为符合输入的格式也是非常好的练习）

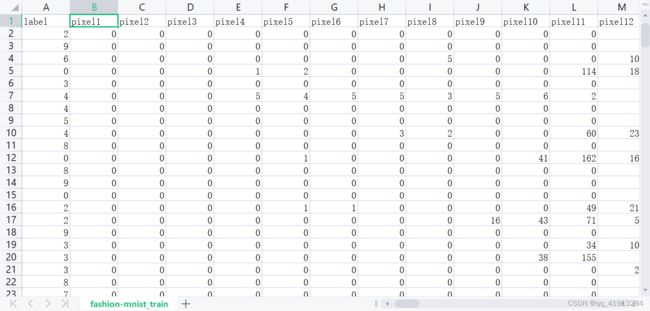
        下载到的csv格式数据打开以后是这样的：

        原本图像的大小是28x28，一共728个像素，因此输入矩阵的规模是60000x729（第一列是标签）。接下来声明一个子类MyDataset，继承自Dataset：

class MyDataset(Dataset):
    def __init__(self,df,transform=None):
        self.df = df
        self.transform = transform
        self.image = df.iloc[:,1:].values.astype(np.unit8)
        self.labels = df.iloc[:,0].values
    
    def __len__(self):
        return len(self.image)
    
    def __getitem__(self, index):
        image = self.image[index].reshape(1,28,28)
        label = int(self.labels[index])
        if self.transform is not None:
            image = self.transform(image)#如果定义了transform操作，可对输入图像进行旋转、缩放等操作
        else:
            image = torch.tensor(image/255.,dype=torch.float)
        label = torch.tensor(label,dtype=torch.long)#转化为tensor进行输入
        return image,label

        把下载的csv数据输入给df把上面定义的类实例化：
 

train_dataflow = pd.read_csv('fashion-mnist_train.csv')
test_dataflow = pd.read_csv('fashion-mnist_test.csv')
train_data = MyDataset(train_dataflow)
test_data = MyDataset(test_dataflow)

        用plt.imshow函数可以把输入的数据转化成图像

        第2步：建立模型

        在定义的模型类中，主要就是两个部分：1.初始化部分，模型每一层的结构就在此构建 2.前向传播，即执行完这一步后最终输出的是预测结果。下面是一些网络具体实现的例子：

卷积网络

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv=nn.Sequential(nn.Conv2d(1,32,5),
                                nn.ReLU(),
                                nn.MaxPool2d(2,stride=2),
                                nn.Dropout(0.3),
                                nn.Conv2d(32,64,5),
                                nn.ReLU(),
                                nn.MaxPool2d(2,stride=2),
                                nn.Dropout(0.3))
        self.fc = nn.Sequential(nn.Linear(64*4*4,512),nn.ReLU(),nn.Linear(512,10))
        
    def forward(self,x):
        x = self.conv(x)
        x = self.view(-1,64*4*4)
        x = self.fc(x)
        return x

model = Net().to(device)

        神经网络结构、参数说明：

        可把卷积神经网络粗略分为卷积部分和全连接部分，卷积部分的构成可以看成：卷积层+激活层+池化层这三部分的叠加（在上面的代码中，还有针对过拟合现象进行优化的Dropout层）。在nn模块中，通过序列式（Sequential）来完成网络的搭建：

        1.卷积，Conv2d，前三个参数分别为：输入通道数、输出通道数、卷积核大小（还有其他参数例如步长、padding可以输入修改）

        2.激活函数ReLU

        3.最大池化，这里设置了核尺寸为2，步长2        

        全连接部分：

        通过两个全连接层，中间用ReLU作为激活函数，把最终的输出维度降为10

        值得一提的是，在第一个卷积层中输入参数为（1，32，5），而后面相应卷积层以及全连接层的参数需要根据计算来确定：原始输入图像尺寸nw*nh*nc=28x28x1（长x宽x通道数），Conv2d中前两个参数是输入和输出的通道，因此这两个通道相关参数前后对应即可；在FC的第一层，输入的形状是64*4*4，这里是把输入的张量展平成1维，64是最后输出的通道数目，4*4是最终的尺寸。

        卷积网络的特性之一：将图像特征不断压缩，而通道数不断增加

        来看一下怎么得到4*4：原始图像是28x28，卷积核的大小是5，一次卷积后28-5+1=24，形状变成24x24；接下来用尺寸为2的核以2为步长做池化，变成12x12；再来一次卷积12-5+1=8，变成8x8；再池化，得到的就是最终的4x4

        至此，模型的搭建准备工作已经完成。内容就暂且写这么多，俺也先消化消化前面的内容，后面的优化模型、训练模型就留到下篇再谈