机器学习| 感知机算法实现/调库实现

通关后做下笔记，方便查看踩过的坑。

第一关：感知机 - 西瓜好坏自动识别

主要的算法思想还是挺直观的：先预设w, b，然后找分错的点，不断修正w, b的值，直到正确率满足要求为止。如图所示：

代码如下：
2022/5/14 21:23更新：第二题发现正则的预处理之后，在第一题也用了同样的操作，发现迭代次数不需要增加的情况下，正确率直接大于0.8。
以下是修改代码：（每次更改所有预测错的点）

#encoding=utf8
import numpy as np
from sklearn.preprocessing import StandardScaler
#构建感知机算法
class Perceptron(object):
    def __init__(self, learning_rate = 0.01, max_iter = 200):
        self.lr = learning_rate
        self.max_iter = max_iter
        self.sc = StandardScaler() #新增
    def fit(self, data, label):
        '''
        input:data(ndarray):训练数据特征
              label(ndarray):训练数据标签
        output:w(ndarray):训练好的权重
               b(ndarry):训练好的偏置
        '''
        #编写感知机训练方法，w为权重，b为偏置
        self.sc.fit(data)
        data = self.sc.transform(data)
        self.w = np.array([1.]*data.shape[1])
        self.b = np.array([1.])
        #********* Begin *********#
        f = (np.dot(data, self.w.T) + self.b) * label
        idx = np.where(f <= 0)  #满足条件(condition)，则输出满足条件 (即非0) 元素的坐标
        iteration = 1
        #f[idx].size:分错点的数量
        while f[idx].size != 0 and iteration <= self.max_iter:
            for i in range(f[idx].shape[0]):
                x = data[idx[0][i], :]
                y = label[idx[0][i]]
                self.w = self.w + self.lr * y * x
                self.b = self.b + self.lr * y
                f = (np.dot(data, self.w.T) + self.b) * label
            f = (np.dot(data, self.w.T) + self.b) * label
            idx = np.where(f <= 0)
            iteration = iteration + 1
            
        #********* End *********#
    def predict(self, data):
        '''
        input:data(ndarray):测试数据特征
        output:predict(ndarray):预测标签
        '''
        #********* Begin *********#
        data = self.sc.transform(data)
        f = np.dot(data, self.w) + self.b
        predict = np.where(f > 0, 1, -1) #f>0,好瓜，否则是坏瓜
        #********* End *********#
        return predict    

每次只更改一个点也可以！！！

#encoding=utf8
import numpy as np
from sklearn.preprocessing import StandardScaler
#构建感知机算法
class Perceptron(object):
    def __init__(self, learning_rate = 0.01, max_iter = 200):
        self.lr = learning_rate
        self.max_iter = max_iter
        self.sc = StandardScaler() #新增
    def fit(self, data, label):
        '''
        input:data(ndarray):训练数据特征
              label(ndarray):训练数据标签
        output:w(ndarray):训练好的权重
               b(ndarry):训练好的偏置
        '''
        #编写感知机训练方法，w为权重，b为偏置
        self.sc.fit(data)
        data = self.sc.transform(data)
        self.w = np.array([1.]*data.shape[1])
        self.b = np.array([1.])
        #********* Begin *********#
        f = (np.dot(data, self.w) + self.b) * label
        idx = np.where(f <= 0)  #满足条件(condition)，则输出满足条件 (即非0) 元素的坐标
        iteration = 1
        while f[idx].size != 0 and iteration <= self.max_iter:
            point = np.random.randint((f[idx].shape[0])) #得到第一维的长度
            x = data[idx[0][point], :]
            y = label[idx[0][point]]
            self.w += self.lr * y * x
            self.b += self.lr * y
            f = (np.dot(data, self.w.T) + self.b) * label
            idx = np.where(f <= 0)
            iteration = iteration + 1
        #print(iteration)
        #print(self.w)
        #print(self.b)
        #********* End *********#
    def predict(self, data):
        '''
        input:data(ndarray):测试数据特征
        output:predict(ndarray):预测标签
        '''
        #********* Begin *********#
        data = self.sc.transform(data)
        f = np.dot(data, self.w) + self.b
        predict = np.where(f > 0, 1, -1) #f>0,好瓜，否则是坏瓜
        #********* End *********#
        return predict     

以下是首次通关代码：

#encoding=utf8
import numpy as np
#构建感知机算法
class Perceptron(object):
    def __init__(self, learning_rate = 0.01, max_iter = 200):
        self.lr = learning_rate
        self.max_iter = max_iter
    def fit(self, data, label):
        '''
        input:data(ndarray):训练数据特征
              label(ndarray):训练数据标签
        output:w(ndarray):训练好的权重
               b(ndarry):训练好的偏置
        '''
        #编写感知机训练方法，w为权重，b为偏置
        self.w = np.array([1.]*data.shape[1])
        self.b = np.array([1.])
        #data.shape=(455, 30)
        #self.w.shape = (30, )
        #********* Begin *********#
        f = (np.dot(data, self.w.T) + self.b) * label
        idx = np.where(f <= 0)  #满足条件(condition)，则输出满足条件 (即非0) 元素的坐标
        iteration = 1
        #f[idx].size:分错点的数量
        self.max_iter = 300 #修改默认迭代次数为300
        while f[idx].size != 0 and iteration <= self.max_iter: #f[idx].shape = (166,)
            for i in range(f[idx].shape[0]):
                x = data[idx[0][i], :]
                y = label[idx[0][i]]
                self.w = self.w + self.lr * y * x
                self.b = self.b + self.lr * y
                f = (np.dot(data, self.w.T) + self.b) * label
            f = (np.dot(data, self.w.T) + self.b) * label
            idx = np.where(f <= 0)
            iteration = iteration + 1
            
        #********* End *********#
    def predict(self, data):
        '''
        input:data(ndarray):测试数据特征
        output:predict(ndarray):预测标签
        '''
        #********* Begin *********#
        f = np.dot(data, self.w) + self.b
        predict = np.where(f > 0, 1, -1) #f>0,好瓜，否则是坏瓜
        #********* End *********#
        return predict    

但是在代码实现的过程中，还要注意：每次迭代是先将所有分错的点把该轮迭代时的w, b修正，而不是每次改一个然后立即进入下一次迭代。否则正确率永远在0.4~0.6左右。

但是这样修改以后还不够，必须将迭代次数改成300才能过。原因未知。
代码思路参考这两篇博客，但是将两篇的思路做了融合：

1. https://cloud.tencent.com/developer/article/1660650
2. https://blog.csdn.net/iwangzhengchao/article/details/78570812

其中第二篇所用point = np.random.randint((f[idx].shape[0]))是将所有分错点的行数随机取一个，毕竟原始数据的shape为(455, 30)。分错的数据行数只会小于455。

这样对于大数据有用，但是对于较小的数据来说，建议还是全部将分错的点都加入进去fine_tune需要求的w,b。这样正确率高一点。这正是第一篇的思路。

学会一个筛选矩阵元素的方法：np.where()


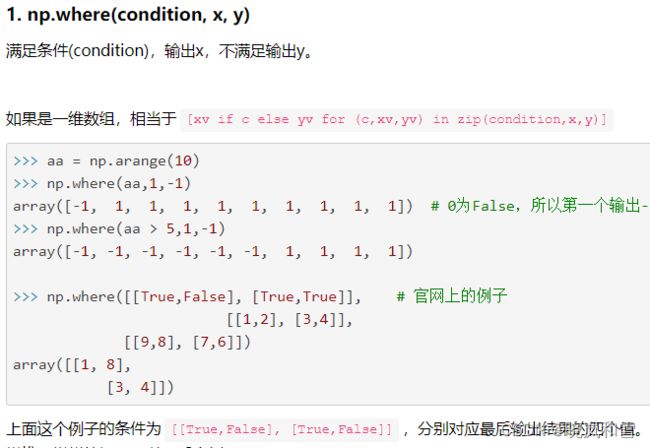
均在上述代码中用到。

第二关 scikit-learn感知机实践 - 癌细胞精准识别

与第一关思路相同，但是调库实现，容易很多。
在数据投入fit以前进行了标准化，正确率迅速提高。
加入标准化前：（前后参数完全相同）

加入后：

代码如下：

#encoding=utf8
import os

if os.path.exists('./step2/result.csv'):
    os.remove('./step2/result.csv')
    
#下面是通关代码
from sklearn.linear_model import Perceptron
from sklearn.preprocessing import StandardScaler
import pandas as pd  
#获取训练数据  
train_data = pd.read_csv('./step2/train_data.csv')  
#获取训练标签  
train_label = pd.read_csv('./step2/train_label.csv')  
train_label = train_label['target']  
#获取测试数据  
test_data = pd.read_csv('./step2/test_data.csv')  #shape(114, 30)

#特征进行标准化
sc = StandardScaler()
sc.fit(train_data)
train_std = sc.transform(train_data)
test_std = sc.transform(test_data)

#训练
pcn = Perceptron(max_iter=30, eta0=1.0)
pcn.fit(train_std, train_label)

#预测
result = pcn.predict(test_std)

#将np.array转换为dataframe写入csv文件，注意序列号必须是'result'
dataframe = pd.DataFrame({'result':result})
dataframe.to_csv("./step2/result.csv",index=False,sep=',')

• StandardScaler归一化原理：(sklearn常用的数据预处理方式之一）