混合策略改进鲸鱼优化算法-附代码
混合策略改进鲸鱼优化算法
文章目录
- 混合策略改进鲸鱼优化算法
-
- 1.鲸鱼优化算法
- 2. 改进鲸鱼优化算法
-
- 2.1 Tent混沌映射
- 2. 2 混合反向学习策略
-
- 2.2.1 透镜成像反向学习策略
- 2.2.2 最优最差反向学习策略
- 2.3 自适应阈值
- 2.4 自适应权重
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要: 为使鲸鱼优化算法在具备摆脱局部最优区域能力的同时提升算法寻优能力,提出一种基于混合策略的改进鲸鱼优化算法。利用混沌的特性对初始种群位置进行优化,使种群个体更加丰富多样,位置分布更加合理;提出一种混合反向学习策略,将透镜成像反向学习策略和最优最差反向学习策略相结合,提高领导者跳出局部最优区域的能力,提高算法的求解精度;出于协调改进算法勘探能力的目的,将自适应概率阈值p’和权重ω 融入到算法中。
1.鲸鱼优化算法
基础鲸鱼算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107559167
2. 改进鲸鱼优化算法
2.1 Tent混沌映射
混沌是非线性系统一种复杂的动态行为, 表现出貌似 无规则、类似随机的现象, 可以利用这种随机性和遍历 性等特点, 来提高算法的性能。其中常用的混沌序列模型 有 Logistic 和 Tent 映射, 很多研究中采用的是 Logistic 映 射, 但相关研究表明 [ 14 , 15 ] { }^{[14,15]} [14,15], Tent 映射比 Logistic 映射拥有 更加均匀的分布, 能使算法拥有更快的收敛速度。所以本 文采用 Tent 映射来产生混沌序列, 表示如下
x n + 1 = { 2 x n , 0 ⩽ x n < 0.5 8 ( 1 − x n ) , 0.5 ⩽ x n ⩽ 1 (9) x_{n+1}=\left\{\begin{array}{l} 2 x_{n}, 0 \leqslant x_{n}<0.5 \\ 8\left(1-x_{n}\right), 0.5 \leqslant x_{n} \leqslant 1 \end{array}\right. \tag{9} xn+1={2xn,0⩽xn<0.58(1−xn),0.5⩽xn⩽1(9)
经伯努利移位变换后表示如下
x n + 1 = ( 2 x n ) m o d 1 (10) x_{n+1}=\left(2 x_{n}\right) \bmod 1 \tag{10} xn+1=(2xn)mod1(10)
因为鲸鱼优化算法的参数少, 模型简单, 而且容易实 现, 而 Tent 映射遍历性和随机性的特点使得算法拥有更加 广泛的搜索范围, 利用这种混沌分布来降低算法存在的不 利影响是十分必要的, 因为它避免了个体在相似区域内进 行大量搜索的情况。
2. 2 混合反向学习策略
为解决算法容易陷入局部最优的问题,有学者提出了反向学习的概念,同时大量研究表明大多数精英粒子的反向解比普通解的反向解更靠近最优解,能够有效跳出局部最优解,本文通过结合透镜成像反向学习策略[17]和最优最差反向学习策略,提出了一种混合反向学习的方法,对WOA中每次更新后的鲸鱼领导者位置进行反向学习操作,一定程度上给算法提供更多的选择条件,进而增加算法避免早熟的概率。
2.2.1 透镜成像反向学习策略
当前解决局部最优问题主要有两种方案,一是在当前最优位置上向其它区域进行寻优,二是放弃当前最优位置,转而向新的区域进行搜索。本文选择第一种手段,引入透镜成像原理来帮助算法跳出局部最优区域.
假设某一空间中, 全局最优位置 X best X_{\text {best }} Xbest 是将一个高度为 h h h 的个体 P P P 投影到 x x x 轴上得到的, 坐标轴的上下限为 a j a_{j} aj 和 b j b_{j} bj 表示当前解第 j j j 维的上下限, 在原点 o o o 上放一个焦距为 f f f 的凸透镜, 通过凸透镜成像可以得到一个高度为 h ∗ h^{*} h∗ 的 P ∗ P^{*} P∗, 此时在 x x x 轴得到通过成像产生的最优位置 X best ∗ X_{\text {best }}^{*} Xbest ∗ (反向点)。 所以由透镜成像原理可以得出
( a j + b j ) / 2 − X best ( t ) X be:t ∗ ( t ) − ( a j + b j ) / 2 = h h ∗ (11) \frac{\left(a_{j}+b_{j}\right) / 2-X_{\text {best }}(t)}{X_{\text {be:t }}^{*}(t)-\left(a_{j}+b_{j}\right) / 2}=\frac{h}{h^{*}} \tag{11} Xbe:t ∗(t)−(aj+bj)/2(aj+bj)/2−Xbest (t)=h∗h(11)
设 h / h ∗ = n h / h^{*}=n h/h∗=n, 通过变换得到 X ∗ X^{*} X∗, 表达式如下
X best ∗ ( t ) = ( a j + b j ) 2 + ( a j + b j ) 2 n − X best ( t ) n (12) X_{\text {best }}^{*}(t)=\frac{\left(a_{j}+b_{j}\right)}{2}+\frac{\left(a_{j}+b_{j}\right)}{2 n}-\frac{X_{\text {best }}(t)}{n} \tag{12} Xbest ∗(t)=2(aj+bj)+2n(aj+bj)−nXbest (t)(12)
由式(12)可以看出, 当 n = 1 n=1 n=1 时的透镜成像反向学习 策略就是一般意义上的反向学习策略, 通过调节 n n n 值来寻 找位置更好的个体, 本文设置 n n n 为 1.2 × 1 0 4 1.2 \times 10^{4} 1.2×104 。由于精英个 体比普通个体拥有更加广阔的搜索区域, 所以当 WOA 陷 人局部最优解时, 对其采用上述透镜成像反向学习机制, 提高算法摆脱局部极值的能力。
2.2.2 最优最差反向学习策略
为增加种群中鲸鱼领导者位置的多样性, 提高算法的 搜索能力, 对全局最差位置的鲸鱼采用随机反向学习的策 略, 公式如下
X worst ∗ ( t ) = a j + rand ⋅ ( b j − X worst ( t ) ) (13) X_{\text {worst }}^{*}(t)=a_{j}+\operatorname{rand} \cdot\left(b_{j}-X_{\text {worst }}(t)\right) \tag{13} Xworst ∗(t)=aj+rand⋅(bj−Xworst (t))(13)
式中: X worst X_{\text {worst }} Xworst 表示当前最差位置向量, rand 是服从 [ 0 , 1 ] [0,1] [0,1] 分布的随机数。
算法每迭代一次, 都通过式(12)和式(13)进行位 置笑选, 通过对比反向学习前后的适应度值大小, 对最优 位置和适应度值进行更新。与精英反向学习相比, 本文选 择的是当前种群中位置最优和最差的两个个体来进行处理, 而精英反向学习中常采用种群中前几个个体进行位置缩放, 但几个差异不大的个体对增加算法跳出局部最优区域的可 能性影响不会很大, 反而会增加算法计算的复杂性, 与最 优最差反向学习策略中固定搜索边界相比, 本文采用动态变化的边界使算法具备更有效的搜索范围,一定程度上能够改善算法寻优精度。
2.3 自适应阈值
为了同步包围和螺旋行进过程, 原始算法设置概率阈 值均为 0.5 0.5 0.5, 通过随机生成的 p p p 值与概率阈值作比较来选 择狩猎策略, 随着迭代次数增加, 这种等概率的捕食方式 会导致算法陷人局部最优等问题, 受文献启发, 本 文提出了一个对数形式的自适应概率阈值 p ′ p^{\prime} p′ 来平衡全局搜 索和局部开发的能力。表达式如下
p ′ = 1 − log 10 ( 1 + 9 t m a x _ i t e r ) (14) p^{\prime}=1-\log _{10}(1+\frac{9t}{{max\_iter }}) \tag{14} p′=1−log10(1+max_iter9t)(14)
式中:max_iter 为最大迭代次数, t t t 为当前迭代次数。
在迭代初期, 自适应阈值较大, 此时 p ⩽ p ′ p \leqslant p^{\prime} p⩽p′, 算法以大 概率且较快的速度完成全局搜索; 到迭代后期, 随着概率 阈值以缓慢的速度减小至 0 , 由于 p > p ′ p>p^{\prime} p>p′, 此时算法将大概 率选择螺旋行进方式对领导者位置进行更新, IWO 通过不 断更新算法中的自适应概率阈值, 使鲸鱼群不断靠近最优 解, 进而提升算法的收敛精度。
2.4 自适应权重
原始 WOA在后期进行局部开发时, 没有相应的权值 对更新公式进行调整, 随着搜索过程的深人可能会导致鲸 鱼个体在理论位置附近停留, 也可能陷人局部极值, 因此 本文把粒子群算法中的惯性权重引人 WOA 中, 对算法位 置更新公式调整如下
ω = ( ω s a r t − ω e n d ) × ( 0.8 × ( 1 − ( t m a x _ i t e r ) k ) ) + ω e n d \omega=\left(\omega_{{sart }}-\omega_{{end }}\right) \times\left(0.8 \times\left(1-\left(\frac{t}{{ max\_iter }}\right)^{k}\right)\right)+\omega_{ {end }} ω=(ωsart−ωend)×(0.8×(1−(max_itert)k))+ωend
式中: t t t 为当前迭代次数, max_iter为最大迭代次数, ω start \omega_{\text {start }} ωstart 表示迭代开始时的初始权值, 即当 t = 0 t=0 t=0 时, ω sart = 0.9 \omega_{\text {sart }}=0.9 ωsart =0.9, ω end \omega_{\text {end }} ωend 表示迭代结束时的权值, 即当 t = t= t= max_iter 时, ω end = \omega_{\text {end }}= ωend = 0.4 , k 0.4, k 0.4,k 为控制因子, 控制 ω \omega ω 曲线的平滑度, 本文 k = 0.6 k=0.6 k=0.6 。 权值 ω \omega ω 随着迭代次数的增加而非线性递减, 当算法在初期 时的权重系数比较大时, 此时具有较强的全局搜索能力; 随着迭代次数的增加, 权重系数在逐渐减小, 此时算法采 用较小权重以螺旋行进方式在最优解邻域内进行搜索, 防 止陷人局部最优。改进 WOA公式如下
X ( t + 1 ) = ω ⋅ X ∗ ( t ) − A ⋅ D ∣ A ∣ < 1 , p < p ′ (16) X(t+1)=\omega \cdot X^{*}(t)-A \cdot D \quad|A|<1, p
X ( t + 1 ) = ω ⋅ X rand − A ⋅ D rand ∣ A ∣ ⩾ 1 , p < p ′ (17) X(t+1)=\omega \cdot X_{\text {rand }}-A \cdot D_{\text {rand }} \quad|A| \geqslant 1, p
X ( t + 1 ) = D ′ ⋅ e b ⋅ cos ( 2 π l ) + ω X ∗ ( t ) p ⩾ p ′ (18) X(t+1)=D^{\prime} \cdot e^{b} \cdot \cos (2 \pi l)+\omega X^{*}(t) \quad p \geqslant p^{\prime}\tag{18} X(t+1)=D′⋅eb⋅cos(2πl)+ωX∗(t)p⩾p′(18)
综上 所 述,本文所提混合策略改进鲸鱼优化算法(IWOA)主要实现流程如下所示:
步骤1 设置算法中鲸鱼种群大小N=30,最大迭代次数 max_iter = 1000 =1000 =1000 。
步骤 2 采用 Tent 混沌映射的策略在搜索空间中初始 化位置分布相对均匀的 N N N 个个体。
步骤 3 根据测试函数 f ( x ) f(x) f(x) 得出混沌种群中 30 个鲸 鱼个体的函数值, 依照得到的函数值大小将整个种群进行 排序, 同时将函数值最小的位置作为最优位置进行保存。
步骤 4 根据式 (14) 和式 (15) 更新参数 p ′ p^{\prime} p′ 和 ω \omega ω, 并 更新算法中 a 、 A 、 C 、 l a 、 A 、 C 、 l a、A、C、l 等相关参数。
步骤 5 通过比较算法中参数 ∣ A ∣ |A| ∣A∣ 的大小和自适应的 概率阈值 p ′ p^{\prime} p′ 与随机生成的 p p p 值的大小, 进而选择相应的更 新方案: 当 p < p ′ p
步骤 6 挑选出当前种群中一个精英个体和一个位置最 差个体, 按式 (12) 和式 (13) 进行混合反向学习, 通过 比较反向操作后的适应度值, 更新全局最优位置和适 应度值。
步骤 7 判断算法是否达满足停止的条件, 若满足则跳 出循环过程, 同时返回当前最优解及适应度值, 反之继续 运行步骤 4 ∼ 4 \sim 4∼ 步骤 6 。
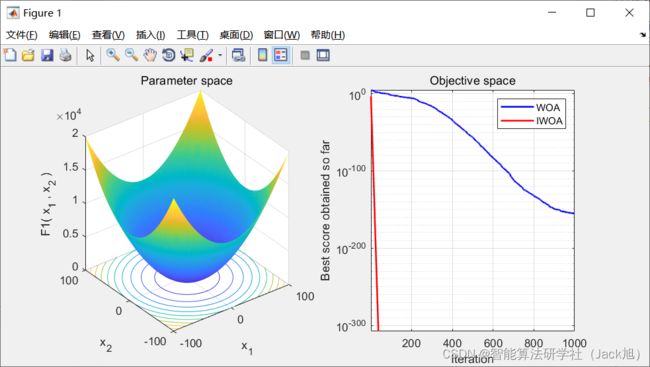
3.实验结果
4.参考文献
[1]徐航,张达敏,王依柔,宋婷婷,樊英.混合策略改进鲸鱼优化算法[J].计算机工程与设计,2020,41(12):3397-3404.