一种改进的鲸鱼优化算法
文章目录
- 一、理论基础
-
- 1、鲸鱼优化算法
- 2、改进的鲸鱼优化算法
-
- (1)准反向学习初始化种群
- (2)非线性收敛因子
- (3)自适应权重策略与随机差分法变异策略
- 二、仿真实验及分析
- 三、参考文献
一、理论基础
1、鲸鱼优化算法
请参考这里。
2、改进的鲸鱼优化算法
基本的鲸鱼优化算法仍然存在着求解精度低、收敛速度慢和易陷入局部最优的缺点。为了克服这些缺点,本文将从种群初始化、位置更新策略以及预防陷入局部最优这三个方面对WOA进行改进。
(1)准反向学习初始化种群
请参考这里。
(2)非线性收敛因子
由于收敛因子 a a a进行线性变化并不能很好地调节全局搜索能力和局部开发能力,因此本文提出来一种非线性收敛因子为 a = 2 − 2 sin ( μ t m a x _ i t e r π + φ ) (1) a=2-2\sin(\mu\frac{t}{\rm{max\_iter}}\pi+\varphi)\tag{1} a=2−2sin(μmax_itertπ+φ)(1)其中, m a x _ i t e r \rm{max\_iter} max_iter为最大迭代次数; t t t为当前迭代次数; μ \mu μ和 φ \varphi φ是其表达式相关参数,选取 μ = 1 2 , φ = 0 \mu=\frac12,\varphi=0 μ=21,φ=0。
(3)自适应权重策略与随机差分法变异策略
鲸鱼优化算法在后期局部开发时易陷入局部最优,出现早熟收敛的现象,为了使算法能够保持种群的多样性并且能够及时跳出局部最优,提出来一种自适应权重策略和随机差分变异策略。
自适应权重策略数学表达式如下: ω = 1 − e t m a x _ i t e r − 1 e − 1 , X ( t + 1 ) = ω ⋅ X p ( t ) − A ⋅ D (2) \omega=1-\frac{e^{\frac{t}{\rm{max\_iter}}}-1}{e-1},\,\,\boldsymbol X(t+1)=\omega\cdot\boldsymbol X_p(t)-\boldsymbol A\cdot \boldsymbol D\tag{2} ω=1−e−1emax_itert−1,X(t+1)=ω⋅Xp(t)−A⋅D(2) X ( t + 1 ) = ω ⋅ X p ( t ) + D ⋅ e b l ⋅ cos ( 2 π l ) (3) \boldsymbol X(t+1)=\omega\cdot\boldsymbol X_p(t)+\boldsymbol D\cdot e^{bl}\cdot\cos(2\pi l)\tag{3} X(t+1)=ω⋅Xp(t)+D⋅ebl⋅cos(2πl)(3)随机差分变异策略如下: X ( t + 1 ) = r 1 × ( X p ( t ) − X ( t ) ) + r 2 × ( X ′ ( t ) − X ( t ) ) (4) \boldsymbol X(t+1)=r_1\times(\boldsymbol X_p(t)-\boldsymbol X(t))+r_2\times(\boldsymbol X'(t)-\boldsymbol X(t))\tag{4} X(t+1)=r1×(Xp(t)−X(t))+r2×(X′(t)−X(t))(4)其中, r 1 r_1 r1和 r 2 r_2 r2均为 [ 0 , 1 ] [0,1] [0,1]的随机数; X ′ ( t ) \boldsymbol X'(t) X′(t)为种群中随机选取的个体。
每个个体都要经过包围捕食、螺旋更新、搜索猎物阶段,当个体进行包围捕食或螺旋更新时采用自适应权重策略去更新位置,之后个体需要通过随机差分变异策略对其再次更新,取其变化前后的最优位置,加快了种群的收敛,有效地防止了种群陷入局部最优。种群通过这两种策略协同工作,使得算法具有更好的寻优效果。
二、仿真实验及分析
将IWOA与WOA、PSO和GSA算法进行对比,实验设置迭代次数均为500次,所有算法种群规模均为30,以文献[1]中表1列出的9个测试函数为例,每个算法独立运行30次,结果显示如下:
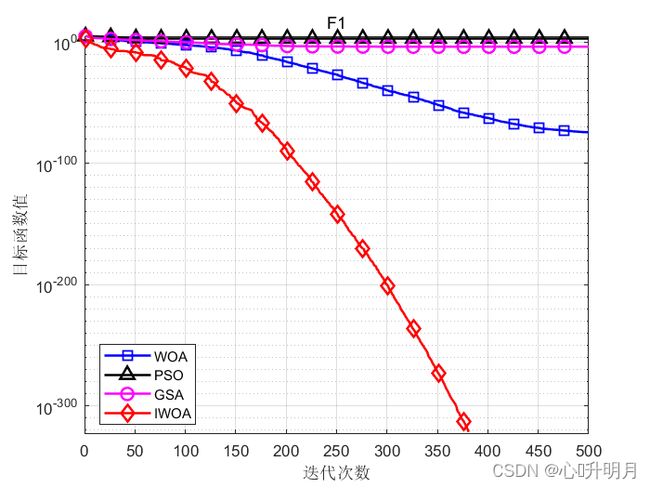





函数:F1
WOA:最差值: 6.0434e-74, 最优值: 1.244e-83, 平均值: 4.8524e-75, 标准差: 1.5191e-74, 秩和检验: 1.2118e-12
PSO:最差值: 1844.6136, 最优值: 319.9645, 平均值: 897.9079, 标准差: 362.3394, 秩和检验: 1.2118e-12
GSA:最差值: 0.0048082, 最优值: 1.0156e-16, 平均值: 0.00016027, 标准差: 0.00087785, 秩和检验: 1.2118e-12
IWOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F2
WOA:最差值: 6.5023e-49, 最优值: 4.0384e-59, 平均值: 3.1087e-50, 标准差: 1.2591e-49, 秩和检验: 3.0199e-11
PSO:最差值: 49.9354, 最优值: 17.0827, 平均值: 25.3533, 标准差: 6.1061, 秩和检验: 3.0199e-11
GSA:最差值: 6.4411, 最优值: 6.1151e-08, 平均值: 0.7822, 标准差: 1.3817, 秩和检验: 3.0199e-11
IWOA:最差值: 5.0507e-300, 最优值: 5.6662e-313, 平均值: 1.7001e-301, 标准差: 0, 秩和检验: 1
函数:F3
WOA:最差值: 86803.9677, 最优值: 10152.6554, 平均值: 41769.2155, 标准差: 15822.3354, 秩和检验: 1.2118e-12
PSO:最差值: 12063.1708, 最优值: 2237.6953, 平均值: 6498.1617, 标准差: 2843.8074, 秩和检验: 1.2118e-12
GSA:最差值: 1797.8533, 最优值: 258.558, 平均值: 947.1683, 标准差: 360.8248, 秩和检验: 1.2118e-12
IWOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
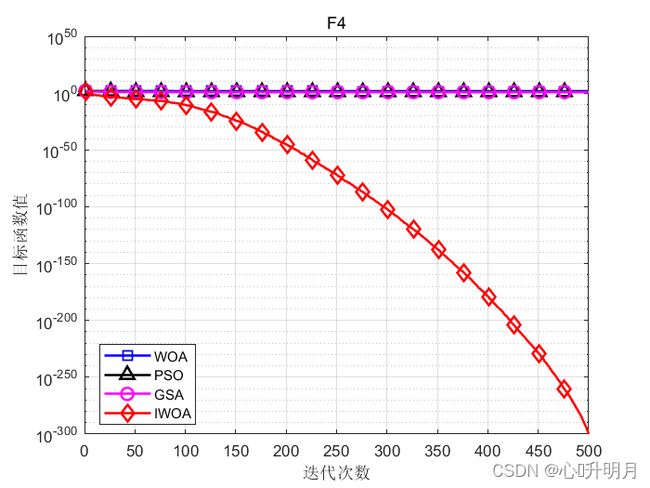
函数:F4
WOA:最差值: 89.3781, 最优值: 0.10516, 平均值: 56.2233, 标准差: 27.7756, 秩和检验: 3.0199e-11
PSO:最差值: 14.9822, 最优值: 6.586, 平均值: 10.8541, 标准差: 1.9351, 秩和检验: 3.0199e-11
GSA:最差值: 12.3007, 最优值: 4.3621, 平均值: 7.4295, 标准差: 2.0443, 秩和检验: 3.0199e-11
IWOA:最差值: 2.8436e-299, 最优值: 9.7449e-310, 平均值: 1.2816e-300, 标准差: 0, 秩和检验: 1
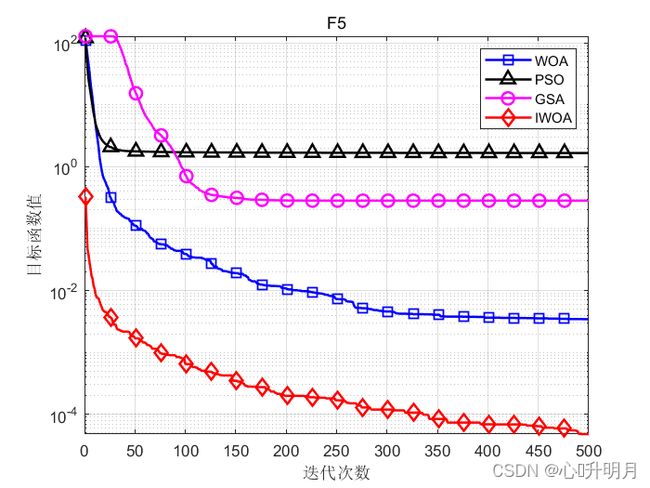
函数:F5
WOA:最差值: 0.017149, 最优值: 2.1308e-05, 平均值: 0.0034382, 标准差: 0.0041751, 秩和检验: 3.4742e-10
PSO:最差值: 3.997, 最优值: 0.55255, 平均值: 1.6619, 标准差: 0.88162, 秩和检验: 3.0199e-11
GSA:最差值: 3.3787, 最优值: 0.044496, 平均值: 0.28219, 标准差: 0.59797, 秩和检验: 3.0199e-11
IWOA:最差值: 0.00019378, 最优值: 2.8772e-06, 平均值: 4.8017e-05, 标准差: 4.4012e-05, 秩和检验: 1
函数:F6
WOA:最差值: -7519.4512, 最优值: -12568.8221, 平均值: -10424.1727, 标准差: 1867.7742, 秩和检验: 7.0881e-08
PSO:最差值: -2168.2069, 最优值: -3829.459, 平均值: -2904.2623, 标准差: 396.5414, 秩和检验: 3.0199e-11
GSA:最差值: -2184.4459, 最优值: -4408.3773, 平均值: -2727.2632, 标准差: 494.7846, 秩和检验: 3.0199e-11
IWOA:最差值: -11287.5412, 最优值: -12569.486, 平均值: -12465.7503, 标准差: 279.0951, 秩和检验: 1
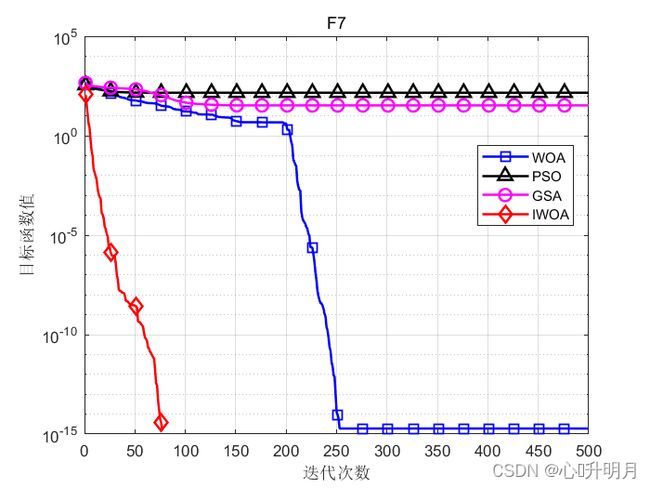
函数:F7
WOA:最差值: 5.6843e-14, 最优值: 0, 平均值: 1.8948e-15, 标准差: 1.0378e-14, 秩和检验: 0.33371
PSO:最差值: 180.5696, 最优值: 113.3323, 平均值: 144.9122, 标准差: 18.0355, 秩和检验: 1.2118e-12
GSA:最差值: 55.7174, 最优值: 21.8891, 平均值: 33.2979, 标准差: 8.4858, 秩和检验: 1.2098e-12
IWOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F8
WOA:最差值: 7.9936e-15, 最优值: 8.8818e-16, 平均值: 3.7303e-15, 标准差: 2.7041e-15, 秩和检验: 7.4605e-07
PSO:最差值: 10.2481, 最优值: 6.2133, 平均值: 8.0176, 标准差: 1.0408, 秩和检验: 1.2118e-12
GSA:最差值: 0.9313, 最优值: 8.0807e-09, 平均值: 0.031043, 标准差: 0.17003, 秩和检验: 1.2118e-12
IWOA:最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
函数:F9
WOA:最差值: 0.15452, 最优值: 0, 平均值: 0.0051507, 标准差: 0.028212, 秩和检验: 0.33371
PSO:最差值: 24.8604, 最优值: 7.3018, 平均值: 13.0565, 标准差: 4.9294, 秩和检验: 1.2118e-12
GSA:最差值: 38.4571, 最优值: 16.8362, 平均值: 26.7235, 标准差: 6.1123, 秩和检验: 1.2118e-12
IWOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
实验结果表明:相比其他优化算法和基本鲸鱼优化算法,改进的鲸鱼优化算法其收敛精度最高,算法稳定性最好。
三、参考文献
[1] 武泽权, 牟永敏. 一种改进的鲸鱼优化算法[J]. 计算机应用研究, 2020, 37(12): 3618-3621.