机器学习笔记之波尔兹曼机(二)梯度求解(正相、负相均采用MCMC)

引言

上一节介绍了波尔兹曼机，并对波尔兹曼机的对数似然梯度进行描述。本节将使用马尔可夫链蒙特卡洛方法对模型参数的梯度进行求解。

回顾：波尔兹曼机

波尔兹曼机的结构表示

这里讨论的含隐变量的波尔兹曼机。基于波尔兹曼机的概率图结构，可以将结点分成两个部分：

• 观测变量集合(Observed Variable)$v$：观测变量的特征是样本集合提供的，可观测的变量信息。
• 隐变量集合(Latent Variable)$h$：隐变量的特征是基于假定的概率图模型产生的特征。

无论是观测变量还是隐变量，在波尔兹曼机中均服从伯努利分布：
$$\{\begin{array}{l}v=(v_1,v_2,\cdots ,v_{\mathcal{D}}{)}^T;v\in \{0,1{\}}^{\mathcal{D}}\\ h=(h_1,h_2,\cdots ,h_{\mathcal{P}}{)}^T;h\in \{0,1{\}}^{\mathcal{P}}\end{array}$$
其中$\mathcal{D},\mathcal{P}$分别表示观测变量，隐变量集合中随机变量的数量，那么基于玻尔兹曼机的约束条件，可以将概率密度函数(联合概率分布)表示如下：
$$\mathcal{P}(\mathcal{X};\theta )=\mathcal{P}(v,h;\theta )=\{\begin{array}{l}\frac{1}{\mathcal{Z}}\exp \{-\mathbb{E}(v,h)\}\\ \mathbb{E}(v,h)=-\left[v^T\mathcal{W}\cdot h+\frac{1}{2}{v}^T\mathcal{L}\cdot v+\frac{1}{2}{h}^T\mathcal{J}\cdot h\right]\end{array}$$
其中模型参数$\theta$由变量之间边的权重$\mathcal{W},\mathcal{L},\mathcal{J}$共同构成。其中：

• $\mathcal{W}$表示观测变量、隐变量之间边的权重组成的矩阵，其中${\mathcal{W}}_{ij}$表示第$i$个观测变量与第$j$个隐变量之间关系的权重信息。
  如果某观测变量与某隐变量之间不存在边相关联，那么对应的权重信息等于0.
  W = [ W i j ] D × P = ( W 11 , W 12 , ⋯   , W 1 P W 21 , W 22 , ⋯   , W 2 P ⋮ W D 1 , W D 2 , ⋯   , W D P ) D × P \mathcal W = [\mathcal W_{ij}]_{\mathcal D \times \mathcal P} = \begin{pmatrix} \mathcal W_{11},\mathcal W_{12},\cdots,\mathcal W_{1 \mathcal P} \\ \mathcal W_{21},\mathcal W_{22},\cdots,\mathcal W_{2 \mathcal P} \\ \vdots\\ \mathcal W_{\mathcal D1},\mathcal W_{\mathcal D2},\cdots,\mathcal W_{\mathcal D \mathcal P} \\ \end{pmatrix}_{\mathcal D \times \mathcal P} W=[Wij​]D×P​= ​W11​,W12​,⋯,W1P​W21​,W22​,⋯,W2P​⋮WD1​,WD2​,⋯,WDP​​ ​D×P​
• 同理，$\mathcal{L},\mathcal{J}$分别表示观测变量、隐变量内部关系的权重信息。基于波尔兹曼机是一个无向图模型，因此对应的$\mathcal{L},\mathcal{J}$均是实对称矩阵，并且对角线上的元素均为0：
  主对角线上元素表示各结点和自身的关联信息。基于波尔兹曼机的条件，模型中的结点不会与自身存在边相连接。
  L = [ L i j ] D × D = ( L 11 = 0 , L 12 , ⋯   , L 1 D L 21 , L 22 = 0 , ⋯   , L 2 D ⋮ L D 1 , L D 2 , ⋯   , L D D = 0 ) D × D J = [ J i j ] P × P = ( J 11 = 0 , J 12 , ⋯   , J 1 P J 21 , J 22 = 0 , ⋯   , J 2 P ⋮ J P 1 , J P 2 , ⋯   , J P P = 0 ) P × P \mathcal L = [\mathcal L_{ij}]_{\mathcal D \times \mathcal D} = \begin{pmatrix} \mathcal L_{11} = 0,\mathcal L_{12},\cdots,\mathcal L_{1\mathcal D} \\ \mathcal L_{21},\mathcal L_{22} = 0,\cdots,\mathcal L_{2\mathcal D} \\ \vdots \\ \mathcal L_{\mathcal D1},\mathcal L_{\mathcal D2},\cdots,\mathcal L_{\mathcal D\mathcal D} = 0 \\ \end{pmatrix}_{\mathcal D \times \mathcal D} \\ \mathcal J = [\mathcal J_{ij}]_{\mathcal P \times \mathcal P} = \begin{pmatrix} \mathcal J_{11} = 0,\mathcal J_{12},\cdots,\mathcal J_{1\mathcal P} \\ \mathcal J_{21},\mathcal J_{22} = 0,\cdots,\mathcal J_{2\mathcal P} \\ \vdots \\ \mathcal J_{\mathcal P1},\mathcal J_{\mathcal P2},\cdots,\mathcal J_{\mathcal P\mathcal P} =0\\ \end{pmatrix}_{\mathcal P \times \mathcal P} L=[Lij​]D×D​= ​L11​=0,L12​,⋯,L1D​L21​,L22​=0,⋯,L2D​⋮LD1​,LD2​,⋯,LDD​=0​ ​D×D​J=[Jij​]P×P​= ​J11​=0,J12​,⋯,J1P​J21​,J22​=0,⋯,J2P​⋮JP1​,JP2​,⋯,JPP​=0​ ​P×P​

模型参数的对数似然梯度

对于波尔兹曼机的模型参数求解(学习任务)问题，由于波尔兹曼机模型结构的复杂性，因而没有办法求解模型参数的解析解。因此，通常使用极大似然估计，通过求解模型参数的对数似然梯度，从而使用梯度上升法来逼近模型参数的最优解。

已知样本集合$\mathcal{V}=\{v^{(1)},v^{(2)},\cdots ,v^{(N)}\};v^{(i)}\in \{0,1{\}}^{\mathcal{D}}$。因此，似然函数$\mathcal{P}(\mathcal{V};\theta )$可表示为如下形式：
$$\begin{array}{rl}\mathcal{P}(\mathcal{V};\theta )& =\frac{1}{N}\log \prod _{i=1}^N\mathcal{P}(v^{(i)};\theta )\\ & =\frac{1}{N}\sum _{i=1}^N\log \mathcal{P}(v^{(i)};\theta )\theta =\{\mathcal{W},\mathcal{L},\mathcal{J}\}\end{array}$$
至此，需要对模型参数求解梯度。关于上述三个模型参数$\mathcal{W},\mathcal{L},\mathcal{J}$的梯度分别表示如下：
从概率密度函数的表达可以看出，这里并没有将$\frac{1}{2}$加上去。但并不影响$\mathcal{L},\mathcal{J}$的梯度方向，原因在于学习率$\eta$同样需要设定，在设定的过程中已经将参数$\frac{1}{2}$包含在内了。
$$\begin{array}{r}{\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(h^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(h^{(i)}{)}^T\right]\\ {\nabla }_{\mathcal{L}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(v^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(v^{(i)}{)}^T\right]\\ {\nabla }_{\mathcal{J}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[h^{(i)}(h^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[h^{(i)}(h^{(i)}{)}^T\right]\end{array}$$
其中${\mathcal{P}}_{data}$表示真实分布，该分布由两部分组成：
$${\mathcal{P}}_{data}\Rightarrow {\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})\cdot {\mathcal{P}}_{model}\left[h^{(i)}\mid v^{(i)}\right]$$
其原因是：这里以模型参数$\mathcal{W}$为例。
$\mathcal{P}(h^{(i)}\mid v^{(i)})$表示隐变量的后验概率，而隐变量仅存在于假定模型中，因而$\mathcal{P}(h^{(i)}\mid v^{(i)})$是模型的分布，记作${\mathcal{P}}_{model}\left[h^{(i)}\mid v^{(i)}\right]$.
$${\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(h^{(i)}{)}^T\right]\approx {\mathbb{E}}_{{\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})}\left\{{\mathbb{E}}_{\mathcal{P}(h^{(i)}\mid v^{(i)})}\left[v^{(i)}(h^{(i)}{)}^T\right]\right\}$$
而${\mathcal{P}}_{model}$表示假定模型的概率分布，它的概率分布具体是联合概率分布：
$${\mathcal{P}}_{model}\Rightarrow {\mathcal{P}}_{model}(h^{(i)},v^{(i)})$$

基于MCMC梯度求解过程存在的问题

此时，各个模型参数的对数似然梯度已经表示出来，可以使用梯度上升法去近似求解最优模型参数：
这里以模型参数$\mathcal{W}$为例。
$$\begin{array}{rl}{\mathcal{W}}^{(t+1)}& \Leftarrow {\mathcal{W}}^{(t)}+\eta {\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]\\ & \Leftarrow {\mathcal{W}}^{(t)}+\eta \left\{{\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(h^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(h^{(i)}{)}^T\right]\right\}\end{array}$$
并且模型参数的梯度${\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]$本身也是一个矩阵形式：
需要注意：上标中的$(i)$表示某一具体样本；下标中的$i$表示其中一个观测变量。例如$v_i^{(i)}$表示具体样本$v^{(i)}$的第$i$个观测变量。
$$\begin{array}{r}{\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\left\{{\nabla }_{{\mathcal{W}}_{ij}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]\right\}}_{\mathcal{D}\times \mathcal{P}}\\ {\nabla }_{{\mathcal{W}}_{ij}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]\end{array}$$
对应图像如下，${\nabla }_{{\mathcal{W}}_{ij}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]$描述的是红色线权重对应的梯度方向。

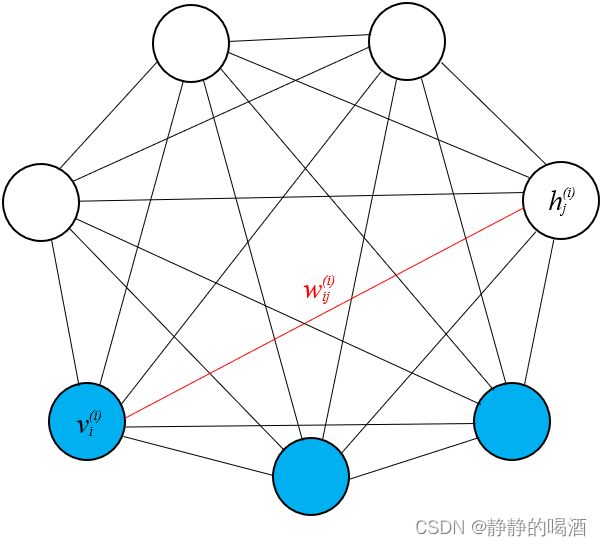
在配分函数——随机最大似然中介绍过，称${\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]$为正相(Positive Phase)，称${\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v_i^{(i)}(h_j^{(i)}{)}^T\right]$为负相(Negative Phase)。
但是波尔兹曼机中对于模型参数梯度的正相的特殊之处在于：$v_i^{(i)}(h_j^{(i)}{)}^T$中的$v_i^{(i)}$来自于真实样本分布${\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})$;而$h_j^{(i)}$来自于隐变量的后验分布${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$。
关于负相基于的分布是关于隐变量、观测变量的联合概率分布${\mathcal{P}}_{model}(h^{(i)},v^{(i)})$。
个人理解：

• 在上述的推导过程中，关于隐变量只能依赖于概率图模型的假设，使得隐变量不会凭空出现。
• 基于步骤1的描述，只要概率分布中含$h^{(i)}$,无论是条件概率还是联合概率分布，都不可能是‘真实分布’${\mathcal{P}}_{data}$。因为真实分布只能观察到‘观测变量’的信息。例如正相中的${\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})$;正相、负相均包含的${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)}),{\mathcal{P}}_{model}(h^{(i)},v^{(i)})$.

回顾受限玻尔兹曼机中对观测变量、隐变量之间关系的约束，可以直接将后验概率$\mathcal{P}(h\mid v)$求解出来：
$$\begin{array}{rl}\mathcal{P}(h^{(i)}\mid v^{(i)})& =\prod _{j=1}^{\mathcal{P}}\mathcal{P}(h_j^{(i)}\mid v^{(i)})\\ \mathcal{P}(h_j^{(i)}\mid v^{(i)})& =\{\begin{array}{l}\text{Sigmoid}\left({\sum }_{i=1}^{\mathcal{D}}{\mathcal{W}}_{ji}^{(i)}{v}_i^{(i)}+c_j^{(i)}\right)h_j^{(i)}=1\\ 1-\text{Sigmoid}\left({\sum }_{i=1}^{\mathcal{D}}{\mathcal{W}}_{ji}^{(i)}{v}_i^{(i)}+c_j^{(i)}\right)h_j^{(i)}=0\end{array}\end{array}$$
此时的后验概率${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$可以直接使用观测变量进行表示，而${\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})$是基于样本集合$\mathcal{V}$产生的，因此关于受限波尔兹曼机的正相是可表示的。

但关于受限波尔兹曼机的负相部分，没有办法对联合概率分布直接进行求解，在受限波尔兹曼机——对数似然梯度求解过程中针对负相的积分问题，采用的是块吉布斯采样方法进行近似求解。由于受限波尔兹曼机中各隐变量之间相互独立，不需要传统采样方式中先固定除采样外的其他所有变量，再对该变量进行采样的方式，而是隐变量之间各采各的，互不影响。
为了增加采样效率，同样使用了对比散度的方式进行优化。

但如果将受限波尔兹曼机泛化至波尔兹曼机，此时由于没有隐变量/观测变量相互独立的约束，对于 ${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$同样没有办法进行求解。至此，无论是正相还是负相，波尔兹曼机都是极难直接求解的。

在当时给出的做法就是马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo,MCMC)，但是这种方式自然是非常棘手的。例如吉布斯采样，随着随机变量数量的增长，它的计算量是指数级别的增加。对于过多的随机变量，它的分布近似过程是十分复杂的。

例如，想要使用MCMC方法近似求解${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$，以上述的全连接波尔兹曼机为例，蓝色点给定的条件下，求解某一白色点的后验概率。这明显是不可求的——因为隐变量不仅仅和观测变量相关联，隐变量自身之间也存在关联，并且作为条件的观测变量之间也存在关联。如果使用因子图的方式对该模型进行分解——很遗憾，该概率图本身就是一个极大团，没有继续向下分解的可能。因而没有办法表示隐变量，并基于隐变量进行采样。

关于单个变量的后验概率

基于上面的介绍，可以知道：仅将观测变量作为条件，求解隐变量的后验概率${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})$是基本不可能的。

能否退而求其次，通过单个变量(观测变量、隐变量)的后验概率去描述${\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)}),{\mathcal{P}}_{model}(v^{(i)},h^{(i)})$呢？
这里单个变量的后验存在两种类型：
需要强调的点：无论$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})$还是$\mathcal{P}(h_j^{(i)}=1\mid v^{(i)},h_{-j}^{(i)})$,它们均只是某一个随机变量的后验概率，而不是隐变量/观测变量的后验概率。

• 某观测变量$v_i^{(i)}$的后验概率；
  $$\begin{array}{r}\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\mathcal{P}(v_i^{(i)}=1\mid h_1^{(i)},\cdots ,h_{\mathcal{P}}^{(i)},v_1^{(i)},\cdots ,v_{i-1}^{(i)},v_{i+1}^{(i)},\cdots ,v_{\mathcal{D}}^{(i)})\end{array}$$
• 某隐变量$h_j^{(i)}$的后验概率；
  $$\mathcal{P}(h_j^{(i)}=1\mid v^{(i)},h_{-j}^{(i)})=\mathcal{P}(h_j^{(i)}=1\mid v_1^{(i)},\cdots ,v_{\mathcal{D}}^{(i)},h_1^{(i)},\cdots ,h_{j-1}^{(i)},h_{j+1}^{(i)},\cdots ,h_{\mathcal{P}}^{(i)})$$

这种表示方式给MCMC提供了有效的操作空间，例如吉布斯采样。假设对$v_i^{(i)}$进行采样的过程中，可以固定除$v_i^{(i)}$之外的所有随机变量。当$v_i^{(i)}$采样结束之后，再继续选择其他随机变量如$v_{i+1}^{(i)}$，再次执行上述操作。直到所有随机变量全部采样过，一次迭代才算结束，继续进行下一次迭代。最终达到平稳分布。
关于吉布斯采样，详见吉布斯采样——传送门

关于单个变量后验概率的推导过程

$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})$ 为例，描述它的推导过程。观察基于玻尔兹曼机条件下，该后验能够表示成什么形式：

• 使用条件概率公式，将$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})$表示为如下形式：
  $$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})=\frac{\mathcal{P}(h^{(i)},v_i^{(i)},v_{-i}^{(i)})}{\mathcal{P}(h^{(i)},v_{-i}^{(i)})}=\frac{\mathcal{P}(h^{(i)},v^{(i)})}{\mathcal{P}(h^{(i)},v_{-i}^{(i)})}$$
• 上式中分子部分明显是玻尔兹曼机的概率密度函数；而分母是概率密度函数将$v_i^{(i)}$积分掉后的结果。将概率密度函数带入，有：
  后续为了方便表达，将$\mathcal{P}(v_i^{(i)}\mid h^{(i)},v_{-i}^{(i)})$使用$\mathcal{I}$表示。
  $$\begin{array}{rl}\mathcal{I}& =\frac{\mathcal{P}(h^{(i)},v^{(i)})}{{\sum }_{v_i^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})}\\ & =\frac{\frac{1}{\mathcal{Z}}\exp \{-\mathbb{E}(v^{(i)},h^{(i)})\}}{{\sum }_{v_i^{(i)}}\frac{1}{\mathcal{Z}}\exp \{-\mathbb{E}(v^{(i)},h^{(i)})\}}\end{array}$$
  观察分布部分，$\mathcal{Z}$是配分函数，它的表示如下：
  $$\mathcal{Z}=\sum _{v^{(i)}}\sum _{h^{(i)}}\exp \{-\mathbb{E}(v^{(i)},h^{(i)})\}$$
  可以看出，配分函数$\mathcal{Z}$与$v_i^{(i)}$之间没有关系，因此可以将$\frac{1}{\mathcal{Z}}$提到${\sum }_{v_i^{(i)}}$前面，最终和分子中的$\frac{1}{\mathcal{Z}}$消掉。然后根据 玻尔兹曼机的定义，将能量函数展开，最终表示如下：
  $$\begin{array}{rl}\mathcal{I}& =\frac{\frac{1}{\mathcal{Z}}\exp \{-\mathbb{E}(v^{(i)},h^{(i)})\}}{\frac{1}{\mathcal{Z}}{\sum }_{v_i^{(i)}}\exp \{-\mathbb{E}(v^{(i)},h^{(i)})\}}\\ & =\frac{\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}+\frac{1}{2}[h^{(i)}{]}^T\mathcal{J}\cdot h^{(i)}\right\}}{{\sum }_{v_i^{(i)}}\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}+\frac{1}{2}[h^{(i)}{]}^T\mathcal{J}\cdot h^{(i)}\right\}}\end{array}$$
• 继续将分子分母的大括号展开：
  注意：$h^{(i)}$和${\sum }_{v_i^{(i)}}$之间没有关系，可以将分母中的$\frac{1}{2}[h^{(i)}{]}^T\mathcal{J}\cdot h^{(i)}$提到积分号前，并与分子中的对应项消掉。
  $$\begin{array}{rl}\mathcal{I}& =\frac{\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}\cdot \exp \{\frac{1}{2}[h^{(i)}{]}^T\mathcal{J}\cdot h^{(i)}\}}{\exp \left\{\frac{1}{2}[h^{(i)}{]}^T\mathcal{J}\cdot h^{(i)}\right\}\cdot {\sum }_{v_i^{(i)}}\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}}\\ & =\frac{\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}}{{\sum }_{v_i^{(i)}}\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}}\end{array}$$
• 由于$v_i^{(i)}$服从伯努利分布，因而分母自然可以写成两项相加的形式$(v_i^{(i)}=0,v_i^{(i)}=1)$，并且在分母中$v_i^{(i)}$已经被积分掉，也就是说$v_i^{(i)}$在分母中不是变量。当$v_i^{(i)}=1$时，仅修改分子中的描述：
  $$\begin{array}{rl}\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})& ={\mathcal{I}}_{v_i^{(i)}=1}\\ & =\frac{\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}{\mid }_{v_i^{(i)}=1}}{\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}{\mid }_{v_i^{(i)}=0}+\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}{\mid }_{v_i^{(i)}=1}}\end{array}$$
  定义符号：$\Delta =\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}$，上式可简写成如下形式：
  $$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\frac{{\Delta }_{v_i^{(i)}=1}}{{\Delta }_{v_i^{(i)}=0}+{\Delta }_{v_i^{(i)}=1}}$$
• 继续观察，暂时先不管$v_i^{(i)}$的取值，先观察$\Delta$。由于$\Delta$中全部是向量乘积的形式，因而将其展开，表示成连加形式：
  $$\begin{array}{rl}\Delta & =\exp \left\{[v^{(i)}{]}^T\mathcal{W}\cdot h^{(i)}+\frac{1}{2}[v^{(i)}{]}^T\mathcal{L}\cdot v^{(i)}\right\}\\ & =\exp \left\{\sum _{l=1}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\frac{1}{2}\sum _{l=1}^{\mathcal{D}}\sum _{k=1}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}\right\}\end{array}$$
  观察上式大括号中的第一项，${\sum }_{l=1}^{\mathcal{D}}{\sum }_{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}$内部一共包含$\mathcal{D}\times \mathcal{P}$个连加项，其中有$\mathcal{P}$个项是和$v_i^{(i)}$相关的：
  $$v_i^{(i)}\Rightarrow \sum _{j=1}^{\mathcal{P}}{v}_i^{(i)}\cdot {\mathcal{W}}_{ij}\cdot h_j^{(i)}$$
  同理，观察上式大括号中的第二项，$\frac{1}{2}{\sum }_{l=1}^{\mathcal{D}}{\sum }_{k=1}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}$内部一共包含$\mathcal{D}\times \mathcal{D}$个连加项，其中和$v_i^{(i)}$相关的项有$2\mathcal{D}-1$项：
  $\mathcal{L}$矩阵第$i$行与第$i$列的项之和。其中$i$行$i$列结果被加重了一次，需要减掉。
  $$v_i^{(i)}\Rightarrow \underset{1项}{v_i^{(i)}\cdot {\mathcal{L}}_{ii}\cdot v_i^{(i)}}+\underset{\mathcal{D}-1项}{\sum _{l\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{li}\cdot v_i^{(i)}}+\underset{\mathcal{D}-1项}{\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}}$$
  实际上，由于$\mathcal{L}$是对角线上元素为0的实对称矩阵，因此，有：
  $$\begin{array}{r}\sum _{l\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{li}\cdot v_i^{(i)}=\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}\\ v_i^{(i)}\Rightarrow \underset{=0}{v_i^{(i)}\cdot {\mathcal{L}}_{ii}\cdot v_i^{(i)}}+2\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}\end{array}$$
• 至此，已经将所有关于$v_i^{(i)}$的项全部找到。最终将$\Delta$中的所有连加项分成与$v_i^{(i)}$相关和不相关的两部分：
  Δ = exp ⁡ { ∑ l ≠ i D ∑ j = 1 P v l ( i ) ⋅ W l j ⋅ h j ( i ) + ∑ j = 1 P v i ( i ) ⋅ W i j ⋅ h j ( i ) + 1 2 [ ∑ l ≠ i D ∑ k ≠ i D v l ( i ) ⋅ L l k ⋅ v k ( i ) + v i ( i ) ⋅ L i i ⋅ v i ( i ) ⏟ = 0 + 2 ∑ k ≠ i D v i ( i ) ⋅ L i k ⋅ v k ( i ) ] } = exp ⁡ { ∑ l ≠ i D ∑ j = 1 P v l ( i ) ⋅ W l j ⋅ h j ( i ) + ∑ j = 1 P v i ( i ) ⋅ W i j ⋅ h j ( i ) + 1 2 ∑ l ≠ i D ∑ k ≠ i D v l ( i ) ⋅ L l k ⋅ v k ( i ) + ∑ k ≠ i D v i ( i ) ⋅ L i k ⋅ v k ( i ) } \begin{aligned} \Delta & = \exp \left\{\sum_{l \neq i}^{\mathcal D} \sum_{j=1}^{\mathcal P} v_l^{(i)} \cdot \mathcal W_{lj} \cdot h_j^{(i)} + \sum_{j=1}^{\mathcal P}v_i^{(i)} \cdot \mathcal W_{ij} \cdot h_j^{(i)} + \frac{1}{2} \left[\sum_{l \neq i}^{\mathcal D}\sum_{k \neq i}^{\mathcal D} v_l^{(i)} \cdot \mathcal L_{lk}\cdot v_k^{(i)} + \underbrace{v_i^{(i)} \cdot \mathcal L_{ii} \cdot v_i^{(i)}}_{=0} + 2\sum_{k \neq i}^{\mathcal D}v_i^{(i)} \cdot \mathcal L_{ik} \cdot v_k^{(i)}\right]\right\} \\ & = \exp \left\{\sum_{l \neq i}^{\mathcal D} \sum_{j=1}^{\mathcal P} v_l^{(i)} \cdot \mathcal W_{lj} \cdot h_j^{(i)} + \sum_{j=1}^{\mathcal P}v_i^{(i)} \cdot \mathcal W_{ij} \cdot h_j^{(i)} + \frac{1}{2} \sum_{l \neq i}^{\mathcal D}\sum_{k \neq i}^{\mathcal D} v_l^{(i)} \cdot \mathcal L_{lk}\cdot v_k^{(i)} + \sum_{k \neq i}^{\mathcal D}v_i^{(i)} \cdot \mathcal L_{ik} \cdot v_k^{(i)}\right\} \end{aligned} Δ​=exp⎩ ⎨ ⎧​l=i∑D​j=1∑P​vl(i)​⋅Wlj​⋅hj(i)​+j=1∑P​vi(i)​⋅Wij​⋅hj(i)​+21​ ​l=i∑D​k=i∑D​vl(i)​⋅Llk​⋅vk(i)​+=0 vi(i)​⋅Lii​⋅vi(i)​​​+2k=i∑D​vi(i)​⋅Lik​⋅vk(i)​ ​⎭ ⎬ ⎫​=exp⎩ ⎨ ⎧​l=i∑D​j=1∑P​vl(i)​⋅Wlj​⋅hj(i)​+j=1∑P​vi(i)​⋅Wij​⋅hj(i)​+21​l=i∑D​k=i∑D​vl(i)​⋅Llk​⋅vk(i)​+k=i∑D​vi(i)​⋅Lik​⋅vk(i)​⎭ ⎬ ⎫​​
  当$v_i^{(i)}=0$时，${\Delta }_{v_i^{(i)}=0}$具体表示为：
  $$\begin{array}{rl}{\Delta }_{v_i^{(i)}=0}& =\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\underset{=0}{\sum _{j=1}^{\mathcal{P}}{v}_i^{(i)}\cdot {\mathcal{W}}_{ij}\cdot h_j^{(i)}}+\frac{1}{2}\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}+\underset{=0}{\sum _{k\ne i}^{\mathcal{D}}{v}_i^{(i)}\cdot {\mathcal{L}}_{ik}\cdot v_k^{(i)}}\right\}\\ & =\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\frac{1}{2}\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}\right\}\end{array}$$
  对应的$v_i^{(i)}=1$时，${\Delta }_{v_i^{(i)}=1}$具体表示为：
  $${\Delta }_{v_i^{(i)}=1}=\exp \left\{\sum _{l\ne i}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\sum _{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+\frac{1}{2}\sum _{l\ne i}^{\mathcal{D}}\sum _{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}+\sum _{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}$$
• 最终，将${\Delta }_{v_i^{(i)}=0},{\Delta }_{v_i^{(i)}=1}$带回$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\frac{{\Delta }_{v_i^{(i)}=1}}{{\Delta }_{v_i^{(i)}=0}+{\Delta }_{v_i^{(i)}=1}}$中，有：
  分子、分母同时除以$\exp \left\{{\sum }_{l\ne i}^{\mathcal{D}}{\sum }_{j=1}^{\mathcal{P}}{v}_l^{(i)}\cdot {\mathcal{W}}_{lj}\cdot h_j^{(i)}+\frac{1}{2}{\sum }_{l\ne i}^{\mathcal{D}}{\sum }_{k\ne i}^{\mathcal{D}}{v}_l^{(i)}\cdot {\mathcal{L}}_{lk}\cdot v_k^{(i)}\right\}$
  $$\mathcal{P}(v_i^{(i)}=1\mid h^{(i)},v_{-i}^{(i)})=\frac{\exp \left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}}{1+\exp \left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}}$$
  基于上式，分子、分母继续同时除以$\exp \left\{{\sum }_{j=1}^{\mathcal{P}}{\mathcal{W}}_{ij}\cdot h_j^{(i)}+{\sum }_{k\ne i}^{\mathcal{D}}{\mathcal{L}}_{ik}\cdot v_k^{(i)}\right\}$,有：
  P ( v i ( i ) = 1 ∣ h ( i ) , v − i ( i ) ) = 1 1 + 1 exp ⁡ { ∑ j = 1 P W i j ⋅ h j ( i ) + ∑ k ≠ i D L i k ⋅ v k ( i ) } = 1 1 + exp ⁡ − { ∑ j = 1 P W i j ⋅ h j ( i ) + ∑ k ≠ i D L i k ⋅ v k ( i ) } = Sigmoid { ∑ j = 1 P W i j ⋅ h j ( i