使用 EANet(外部注意力转换器)进行图像分类
mage classification with EANet (External Attention Transformer
使用 EANet(外部注意力转换器)进行图像分类
介绍
此示例实现了用于图像分类的EANet 模型,并在 CIFAR-100 数据集上进行了演示。EANet 引入了一种新的注意力机制,称为外部注意力,基于两个外部的、小型的、可学习的和共享的内存,只需使用两个级联的线性层和两个归一化层即可轻松实现。它方便地取代了现有架构中使用的自我注意。外部注意力具有线性复杂性,因为它只隐含地考虑所有样本之间的相关性。此示例需要 TensorFlow 2.5 或更高版本,以及 TensorFlow Addons包,可以使用以下命令安装:
pip install -U tensorflow-addons
设置
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import tensorflow_addons as tfa
import matplotlib.pyplot as plt
准备数据
num_classes = 100
input_shape = (32, 32, 3)
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar100.load_data()
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print(f"x_train shape: {x_train.shape} - y_train shape: {y_train.shape}")
print(f"x_test shape: {x_test.shape} - y_test shape: {y_test.shape}")
x_train shape: (50000, 32, 32, 3) - y_train shape: (50000, 100) x_test shape: (10000, 32, 32, 3) - y_test shape: (10000, 100) 配置超参数
weight_decay = 0.0001
learning_rate = 0.001
label_smoothing = 0.1
validation_split = 0.2
batch_size = 128
num_epochs = 50
patch_size = 2 # Size of the patches to be extracted from the input images.
num_patches = (input_shape[0] // patch_size) ** 2 # Number of patch
embedding_dim = 64 # Number of hidden units.
mlp_dim = 64
dim_coefficient = 4
num_heads = 4
attention_dropout = 0.2
projection_dropout = 0.2
num_transformer_blocks = 8 # Number of repetitions of the transformer layer
print(f"Patch size: {patch_size} X {patch_size} = {patch_size ** 2} ")
print(f"Patches per image: {num_patches}")
Patch size: 2 X 2 = 4 Patches per image: 256 使用数据增强
data_augmentation = keras.Sequential(
[
layers.Normalization(),
layers.RandomFlip("horizontal"),
layers.RandomRotation(factor=0.1),
layers.RandomContrast(factor=0.1),
layers.RandomZoom(height_factor=0.2, width_factor=0.2),
],
name="data_augmentation",
)
# Compute the mean and the variance of the training data for normalization.
data_augmentation.layers[0].adapt(x_train)
实现补丁提取和编码层
class PatchExtract(layers.Layer):
def __init__(self, patch_size, **kwargs):
super(PatchExtract, self).__init__(**kwargs)
self.patch_size = patch_size
def call(self, images):
batch_size = tf.shape(images)[0]
patches = tf.image.extract_patches(
images=images,
sizes=(1, self.patch_size, self.patch_size, 1),
strides=(1, self.patch_size, self.patch_size, 1),
rates=(1, 1, 1, 1),
padding="VALID",
)
patch_dim = patches.shape[-1]
patch_num = patches.shape[1]
return tf.reshape(patches, (batch_size, patch_num * patch_num, patch_dim))
class PatchEmbedding(layers.Layer):
def __init__(self, num_patch, embed_dim, **kwargs):
super(PatchEmbedding, self).__init__(**kwargs)
self.num_patch = num_patch
self.proj = layers.Dense(embed_dim)
self.pos_embed = layers.Embedding(input_dim=num_patch, output_dim=embed_dim)
def call(self, patch):
pos = tf.range(start=0, limit=self.num_patch, delta=1)
return self.proj(patch) + self.pos_embed(pos)
实施外部attention块
def external_attention(
x, dim, num_heads, dim_coefficient=4, attention_dropout=0, projection_dropout=0
):
_, num_patch, channel = x.shape
assert dim % num_heads == 0
num_heads = num_heads * dim_coefficient
x = layers.Dense(dim * dim_coefficient)(x)
# create tensor [batch_size, num_patches, num_heads, dim*dim_coefficient//num_heads]
x = tf.reshape(
x, shape=(-1, num_patch, num_heads, dim * dim_coefficient // num_heads)
)
x = tf.transpose(x, perm=[0, 2, 1, 3])
# a linear layer M_k
attn = layers.Dense(dim // dim_coefficient)(x)
# normalize attention map
attn = layers.Softmax(axis=2)(attn)
# dobule-normalization
attn = attn / (1e-9 + tf.reduce_sum(attn, axis=-1, keepdims=True))
attn = layers.Dropout(attention_dropout)(attn)
# a linear layer M_v
x = layers.Dense(dim * dim_coefficient // num_heads)(attn)
x = tf.transpose(x, perm=[0, 2, 1, 3])
x = tf.reshape(x, [-1, num_patch, dim * dim_coefficient])
# a linear layer to project original dim
x = layers.Dense(dim)(x)
x = layers.Dropout(projection_dropout)(x)
return x
实现 MLP 块
def mlp(x, embedding_dim, mlp_dim, drop_rate=0.2):
x = layers.Dense(mlp_dim, activation=tf.nn.gelu)(x)
x = layers.Dropout(drop_rate)(x)
x = layers.Dense(embedding_dim)(x)
x = layers.Dropout(drop_rate)(x)
return x
实现 Transformer 块
def transformer_encoder(
x,
embedding_dim,
mlp_dim,
num_heads,
dim_coefficient,
attention_dropout,
projection_dropout,
attention_type="external_attention",
):
residual_1 = x
x = layers.LayerNormalization(epsilon=1e-5)(x)
if attention_type == "external_attention":
x = external_attention(
x,
embedding_dim,
num_heads,
dim_coefficient,
attention_dropout,
projection_dropout,
)
elif attention_type == "self_attention":
x = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=embedding_dim, dropout=attention_dropout
)(x, x)
x = layers.add([x, residual_1])
residual_2 = x
x = layers.LayerNormalization(epsilon=1e-5)(x)
x = mlp(x, embedding_dim, mlp_dim)
x = layers.add([x, residual_2])
return x
实现 EANet 模型
EANet 模型利用外部关注。传统 self attention 的计算复杂度为O(d * N ** 2),其中d为嵌入大小,N为补丁个数。作者发现大多数像素仅与少数其他像素密切相关,并且N注意力N矩阵可能是多余的。因此,他们提出了一个外部注意模块作为替代方案,其中外部注意的计算复杂度为O(d * S * N). 作为超参数,所提出的算法在像素数上是线性的d。S其实这相当于一个drop patch操作,因为一张图片中一个patch所包含的很多信息都是多余的,不重要的。
def get_model(attention_type="external_attention"):
inputs = layers.Input(shape=input_shape)
# Image augment
x = data_augmentation(inputs)
# Extract patches.
x = PatchExtract(patch_size)(x)
# Create patch embedding.
x = PatchEmbedding(num_patches, embedding_dim)(x)
# Create Transformer block.
for _ in range(num_transformer_blocks):
x = transformer_encoder(
x,
embedding_dim,
mlp_dim,
num_heads,
dim_coefficient,
attention_dropout,
projection_dropout,
attention_type,
)
x = layers.GlobalAvgPool1D()(x)
outputs = layers.Dense(num_classes, activation="softmax")(x)
model = keras.Model(inputs=inputs, outputs=outputs)
return model
在 CIFAR-100 上训练
model = get_model(attention_type="external_attention")
model.compile(
loss=keras.losses.CategoricalCrossentropy(label_smoothing=label_smoothing),
optimizer=tfa.optimizers.AdamW(
learning_rate=learning_rate, weight_decay=weight_decay
),
metrics=[
keras.metrics.CategoricalAccuracy(name="accuracy"),
keras.metrics.TopKCategoricalAccuracy(5, name="top-5-accuracy"),
],
)
history = model.fit(
x_train,
y_train,
batch_size=batch_size,
epochs=num_epochs,
validation_split=validation_split,
)
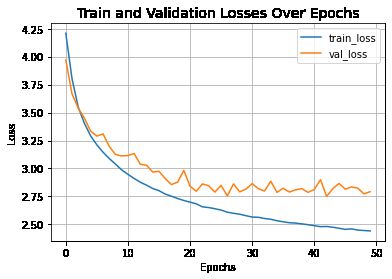
Epoch 1/50 313/313 [==============================] - 40s 95ms/step - loss: 4.2091 - accuracy: 0.0723 - top-5-accuracy: 0.2384 - val_loss: 3.9706 - val_accuracy: 0.1153 - val_top-5-accuracy: 0.3336 Epoch 2/50 313/313 [==============================] - 29s 91ms/step - loss: 3.8028 - accuracy: 0.1427 - top-5-accuracy: 0.3871 - val_loss: 3.6672 - val_accuracy: 0.1829 - val_top-5-accuracy: 0.4513 Epoch 3/50 313/313 [==============================] - 29s 93ms/step - loss: 3.5493 - accuracy: 0.1978 - top-5-accuracy: 0.4805 - val_loss: 3.5402 - val_accuracy: 0.2141 - val_top-5-accuracy: 0.5038 Epoch 4/50 313/313 [==============================] - 29s 93ms/step - loss: 3.4029 - accuracy: 0.2355 - top-5-accuracy: 0.5328 - val_loss: 3.4496 - val_accuracy: 0.2354 - val_top-5-accuracy: 0.5316 Epoch 5/50 313/313 [==============================] - 29s 92ms/step - loss: 3.2917 - accuracy: 0.2636 - top-5-accuracy: 0.5678 - val_loss: 3.3342 - val_accuracy: 0.2699 - val_top-5-accuracy: 0.5679 Epoch 6/50 313/313 [==============================] - 29s 92ms/step - loss: 3.2116 - accuracy: 0.2830 - top-5-accuracy: 0.5921 - val_loss: 3.2896 - val_accuracy: 0.2749 - val_top-5-accuracy: 0.5874 Epoch 7/50 313/313 [==============================] - 28s 90ms/step - loss: 3.1453 - accuracy: 0.2980 - top-5-accuracy: 0.6100 - val_loss: 3.3090 - val_accuracy: 0.2857 - val_top-5-accuracy: 0.5831 Epoch 8/50 313/313 [==============================] - 29s 94ms/step - loss: 3.0889 - accuracy: 0.3121 - top-5-accuracy: 0.6266 - val_loss: 3.1969 - val_accuracy: 0.2975 - val_top-5-accuracy: 0.6082 Epoch 9/50 313/313 [==============================] - 29s 92ms/step - loss: 3.0390 - accuracy: 0.3252 - top-5-accuracy: 0.6441 - val_loss: 3.1249 - val_accuracy: 0.3175 - val_top-5-accuracy: 0.6330 Epoch 10/50 313/313 [==============================] - 29s 92ms/step - loss: 2.9871 - accuracy: 0.3365 - top-5-accuracy: 0.6615 - val_loss: 3.1121 - val_accuracy: 0.3200 - val_top-5-accuracy: 0.6374 Epoch 11/50 313/313 [==============================] - 29s 92ms/step - loss: 2.9476 - accuracy: 0.3489 - top-5-accuracy: 0.6697 - val_loss: 3.1156 - val_accuracy: 0.3268 - val_top-5-accuracy: 0.6421 Epoch 12/50 313/313 [==============================] - 29s 91ms/step - loss: 2.9106 - accuracy: 0.3576 - top-5-accuracy: 0.6783 - val_loss: 3.1337 - val_accuracy: 0.3226 - val_top-5-accuracy: 0.6389 Epoch 13/50 313/313 [==============================] - 29s 92ms/step - loss: 2.8772 - accuracy: 0.3662 - top-5-accuracy: 0.6871 - val_loss: 3.0373 - val_accuracy: 0.3348 - val_top-5-accuracy: 0.6624 Epoch 14/50 313/313 [==============================] - 29s 92ms/step - loss: 2.8508 - accuracy: 0.3756 - top-5-accuracy: 0.6944 - val_loss: 3.0297 - val_accuracy: 0.3441 - val_top-5-accuracy: 0.6643 Epoch 15/50 313/313 [==============================] - 28s 90ms/step - loss: 2.8211 - accuracy: 0.3821 - top-5-accuracy: 0.7034 - val_loss: 2.9680 - val_accuracy: 0.3604 - val_top-5-accuracy: 0.6847 Epoch 16/50 313/313 [==============================] - 28s 90ms/step - loss: 2.8017 - accuracy: 0.3864 - top-5-accuracy: 0.7090 - val_loss: 2.9746 - val_accuracy: 0.3584 - val_top-5-accuracy: 0.6855 Epoch 17/50 313/313 [==============================] - 29s 91ms/step - loss: 2.7714 - accuracy: 0.3962 - top-5-accuracy: 0.7169 - val_loss: 2.9104 - val_accuracy: 0.3738 - val_top-5-accuracy: 0.6940 Epoch 18/50 313/313 [==============================] - 29s 92ms/step - loss: 2.7523 - accuracy: 0.4008 - top-5-accuracy: 0.7204 - val_loss: 2.8560 - val_accuracy: 0.3861 - val_top-5-accuracy: 0.7115 Epoch 19/50 313/313 [==============================] - 28s 91ms/step - loss: 2.7320 - accuracy: 0.4051 - top-5-accuracy: 0.7263 - val_loss: 2.8780 - val_accuracy: 0.3820 - val_top-5-accuracy: 0.7101 Epoch 20/50 313/313 [==============================] - 28s 90ms/step - loss: 2.7139 - accuracy: 0.4114 - top-5-accuracy: 0.7290 - val_loss: 2.9831 - val_accuracy: 0.3694 - val_top-5-accuracy: 0.6922 Epoch 21/50 313/313 [==============================] - 28s 91ms/step - loss: 2.6991 - accuracy: 0.4142 - top-5-accuracy: 0.7335 - val_loss: 2.8420 - val_accuracy: 0.3968 - val_top-5-accuracy: 0.7138 Epoch 22/50 313/313 [==============================] - 29s 91ms/step - loss: 2.6842 - accuracy: 0.4195 - top-5-accuracy: 0.7377 - val_loss: 2.7965 - val_accuracy: 0.4088 - val_top-5-accuracy: 0.7266 Epoch 23/50 313/313 [==============================] - 28s 91ms/step - loss: 2.6571 - accuracy: 0.4273 - top-5-accuracy: 0.7436 - val_loss: 2.8620 - val_accuracy: 0.3947 - val_top-5-accuracy: 0.7155 Epoch 24/50 313/313 [==============================] - 29s 91ms/step - loss: 2.6508 - accuracy: 0.4277 - top-5-accuracy: 0.7469 - val_loss: 2.8459 - val_accuracy: 0.3963 - val_top-5-accuracy: 0.7150 Epoch 25/50 313/313 [==============================] - 28s 90ms/step - loss: 2.6403 - accuracy: 0.4283 - top-5-accuracy: 0.7520 - val_loss: 2.7886 - val_accuracy: 0.4128 - val_top-5-accuracy: 0.7283 Epoch 26/50 313/313 [==============================] - 29s 92ms/step - loss: 2.6281 - accuracy: 0.4353 - top-5-accuracy: 0.7523 - val_loss: 2.8493 - val_accuracy: 0.4026 - val_top-5-accuracy: 0.7153 Epoch 27/50 313/313 [==============================] - 29s 92ms/step - loss: 2.6092 - accuracy: 0.4403 - top-5-accuracy: 0.7580 - val_loss: 2.7539 - val_accuracy: 0.4186 - val_top-5-accuracy: 0.7392 Epoch 28/50 313/313 [==============================] - 29s 91ms/step - loss: 2.5992 - accuracy: 0.4423 - top-5-accuracy: 0.7600 - val_loss: 2.8625 - val_accuracy: 0.3964 - val_top-5-accuracy: 0.7174 Epoch 29/50 313/313 [==============================] - 28s 90ms/step - loss: 2.5913 - accuracy: 0.4456 - top-5-accuracy: 0.7598 - val_loss: 2.7911 - val_accuracy: 0.4162 - val_top-5-accuracy: 0.7329 Epoch 30/50 313/313 [==============================] - 29s 92ms/step - loss: 2.5780 - accuracy: 0.4480 - top-5-accuracy: 0.7649 - val_loss: 2.8158 - val_accuracy: 0.4118 - val_top-5-accuracy: 0.7288 Epoch 31/50 313/313 [==============================] - 28s 91ms/step - loss: 2.5657 - accuracy: 0.4547 - top-5-accuracy: 0.7661 - val_loss: 2.8651 - val_accuracy: 0.4056 - val_top-5-accuracy: 0.7217 Epoch 32/50 313/313 [==============================] - 29s 91ms/step - loss: 2.5637 - accuracy: 0.4480 - top-5-accuracy: 0.7681 - val_loss: 2.8190 - val_accuracy: 0.4094 - val_top-5-accuracy: 0.7267 Epoch 33/50 313/313 [==============================] - 29s 92ms/step - loss: 2.5525 - accuracy: 0.4545 - top-5-accuracy: 0.7693 - val_loss: 2.7985 - val_accuracy: 0.4216 - val_top-5-accuracy: 0.7303 Epoch 34/50 313/313 [==============================] - 28s 91ms/step - loss: 2.5462 - accuracy: 0.4579 - top-5-accuracy: 0.7721 - val_loss: 2.8865 - val_accuracy: 0.4016 - val_top-5-accuracy: 0.7204 Epoch 35/50 313/313 [==============================] - 29s 92ms/step - loss: 2.5329 - accuracy: 0.4616 - top-5-accuracy: 0.7740 - val_loss: 2.7862 - val_accuracy: 0.4232 - val_top-5-accuracy: 0.7389 Epoch 36/50 313/313 [==============================] - 28s 90ms/step - loss: 2.5234 - accuracy: 0.4610 - top-5-accuracy: 0.7765 - val_loss: 2.8234 - val_accuracy: 0.4134 - val_top-5-accuracy: 0.7312 Epoch 37/50 313/313 [==============================] - 29s 91ms/step - loss: 2.5152 - accuracy: 0.4663 - top-5-accuracy: 0.7774 - val_loss: 2.7894 - val_accuracy: 0.4161 - val_top-5-accuracy: 0.7376 Epoch 38/50 313/313 [==============================] - 29s 92ms/step - loss: 2.5117 - accuracy: 0.4674 - top-5-accuracy: 0.7790 - val_loss: 2.8091 - val_accuracy: 0.4142 - val_top-5-accuracy: 0.7360 Epoch 39/50 313/313 [==============================] - 28s 90ms/step - loss: 2.5047 - accuracy: 0.4681 - top-5-accuracy: 0.7805 - val_loss: 2.8199 - val_accuracy: 0.4167 - val_top-5-accuracy: 0.7299 Epoch 40/50 313/313 [==============================] - 28s 90ms/step - loss: 2.4974 - accuracy: 0.4697 - top-5-accuracy: 0.7819 - val_loss: 2.7864 - val_accuracy: 0.4247 - val_top-5-accuracy: 0.7402 Epoch 41/50 313/313 [==============================] - 28s 90ms/step - loss: 2.4889 - accuracy: 0.4749 - top-5-accuracy: 0.7854 - val_loss: 2.8120 - val_accuracy: 0.4217 - val_top-5-accuracy: 0.7358 Epoch 42/50 313/313 [==============================] - 28s 90ms/step - loss: 2.4799 - accuracy: 0.4771 - top-5-accuracy: 0.7866 - val_loss: 2.9003 - val_accuracy: 0.4038 - val_top-5-accuracy: 0.7170 Epoch 43/50 313/313 [==============================] - 28s 90ms/step - loss: 2.4814 - accuracy: 0.4770 - top-5-accuracy: 0.7868 - val_loss: 2.7504 - val_accuracy: 0.4260 - val_top-5-accuracy: 0.7457 Epoch 44/50 313/313 [==============================] - 28s 91ms/step - loss: 2.4747 - accuracy: 0.4757 - top-5-accuracy: 0.7870 - val_loss: 2.8207 - val_accuracy: 0.4166 - val_top-5-accuracy: 0.7363 Epoch 45/50 313/313 [==============================] - 28s 90ms/step - loss: 2.4653 - accuracy: 0.4809 - top-5-accuracy: 0.7924 - val_loss: 2.8663 - val_accuracy: 0.4130 - val_top-5-accuracy: 0.7209 Epoch 46/50 313/313 [==============================] - 28s 90ms/step - loss: 2.4554 - accuracy: 0.4825 - top-5-accuracy: 0.7929 - val_loss: 2.8145 - val_accuracy: 0.4250 - val_top-5-accuracy: 0.7357 Epoch 47/50 313/313 [==============================] - 29s 91ms/step - loss: 2.4602 - accuracy: 0.4823 - top-5-accuracy: 0.7919 - val_loss: 2.8352 - val_accuracy: 0.4189 - val_top-5-accuracy: 0.7365 Epoch 48/50 313/313 [==============================] - 28s 91ms/step - loss: 2.4493 - accuracy: 0.4848 - top-5-accuracy: 0.7933 - val_loss: 2.8246 - val_accuracy: 0.4160 - val_top-5-accuracy: 0.7362 Epoch 49/50 313/313 [==============================] - 28s 91ms/step - loss: 2.4454 - accuracy: 0.4846 - top-5-accuracy: 0.7958 - val_loss: 2.7731 - val_accuracy: 0.4320 - val_top-5-accuracy: 0.7436 Epoch 50/50 313/313 [==============================] - 29s 92ms/step - loss: 2.4418 - accuracy: 0.4848 - top-5-accuracy: 0.7951 - val_loss: 2.7926 - val_accuracy: 0.4317 - val_top-5-accuracy: 0.7410 让我们可视化模型的训练进度。
plt.plot(history.history["loss"], label="train_loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Train and Validation Losses Over Epochs", fontsize=14)
plt.legend()
plt.grid()
plt.show()
让我们在 CIFAR-100 上显示测试的最终结果。
loss, accuracy, top_5_accuracy = model.evaluate(x_test, y_test)
print(f"Test loss: {round(loss, 2)}")
print(f"Test accuracy: {round(accuracy * 100, 2)}%")
print(f"Test top 5 accuracy: {round(top_5_accuracy * 100, 2)}%")
313/313 [==============================] - 6s 21ms/step - loss: 2.7574 - accuracy: 0.4391 - top-5-accuracy: 0.7471 Test loss: 2.76 Test accuracy: 43.91% Test top 5 accuracy: 74.71% EANet 只是将 Vit 中的自我关注替换为外部关注。传统的 Vit 在训练 50 个 epoch 后达到了约 73% 的测试 top-5 准确率和约 41 个 top-1 准确率,但参数为 0.6M。在相同的实验环境和相同的超参数下,我们刚刚训练的 EANet 模型只有 0.3M 个参数,它使我们的测试 top-5 准确率达到了 ~73%,top-1 准确率达到了 ~43%。这充分证明了外部关注的有效性。我们只展示了 EANet 的训练过程,你可以在相同的实验条件下训练 Vit 并观察测试结果。