数据科学与工程理论基础复习提纲

一、Sketch

1.1 简单抽样算法

1.1.1 核心思想

对于到达的元素$a_i$，以概率$p=M/m$对该元素的频数加1。

• $M$：抽样后的数据流大小
• $m$：原始数据流大小

1.1.2 操作

• 更新：当元素$a_i$到达时，以$p$的概率更新$c_i$的值；以$1-p$的概率保持$c_i$的值不变；
• 估计元素频数：返回元素频数数组，其中每个元素的频数为$\widehat{f_i}=c_i/p$；

1.1.3 性能

• 空间需求：$M=O(\frac{mlog(\frac{1}{\delta })}{{ϵ}^2})$，所需空间与数据流大小有关

1.2 Basic Count Sketch算法

1.2.1 核心思想

维护一个计数数组$C$和两个哈希函数$h(\cdot )、g(\cdot )$

• $h(\cdot )$：将$n$个元素均匀映射到$k$个位置
• $g(\cdot )$：将$n$个元素映射为$-1$和$+1$

1.2.2 特点

• 期望$E(\widehat{f_a})=f_a$，即输出结果为$f_a$的无偏估计；
• 方差$Var(\widehat{f_a})=\frac{||f_{-a}|{|}_2^2}{k}$，随着$k$值增大，即存储计数数组的空间增大，方差将随之减小；

1.2.3 性能

• 空间需求：$k=O(\frac{1}{{ϵ}^2\delta })$，与数据流大小无关

1.3 Count Sketch算法

1.3.1 核心思想

在Count Sketch基础上，将哈希函数个数增加到$t$个，将每个元素都映射到$t$个位置上，再区$t$个位置上频数估计的中位数。

1.4 Count-Min Sketch算法

1.4.1 核心思想

• 维护一个宽度为$w$、深度为$d$的计数器数组；
• 另有$d$个哈希函数；

1.4.2 特点

• 放弃了频数的无偏估计(Count Sketch)；
• 获得了更为高效的频数估计；
• $E[X_i]=\frac{||f_{-a}|{|}_1}{k}$
• $P[\widehat{f_a}-f_a\ge ϵ||f_{-a}|{|}_1]=P[min\{X_1,...X_d\}\ge ϵ||f_{-a}|{|}_1]={\prod }_{i=1}^{d}P[X_i\ge ϵ||f_{-a}|{|}_1]\le \frac{1}{(kϵ{)}^d}$

1.4.3 性能

• 计数器个数$M=O(\frac{log(\frac{1}{\delta })}{ϵ})$

二、整数规划

2.1 整数规划

2.1.1 0-1变量

2.1.1.1 概念

很多问题中，决策变量取值只能为1或0。与$x_i\in \{0,1\}$等价的说法有$0\le x_i\le 1$且$x_i\in \mathbf{Z}$。

2.1.1.2 利用0-1变量表示互相排斥的约束条件

例1：假设两个约束通过逻辑或运算进行了组合
$$x\le 2或x\ge 6$$
引入0-1变量$w$：
$$w=\{\begin{array}{r}1,x\le 2\\ 0,x\ge 6\end{array}$$
和一个足够大的整数$M$可以将约束条件改写成：
$$\begin{gathered} x\le 2+M(1-w) \\ x\ge 6-Mw \\ w\in \{0,1\} \end{gathered}$$
例2：假设两个约束条件通过逻辑或运算进行了组合
$$x_1+2x_2\ge 12或4x_1-10x_3\le 1$$
引入0-1变量$w$：
$$w=\{\begin{array}{r}1,x_1+2x_2\ge 12\\ 0,4x_1-10x_3\le 1\end{array}$$
可以改写成:
$$\begin{gathered} x_1+2x_2\ge 12-M(1-w) \\ 4x_1-10x_3\le 1+Mw \\ w\in \{0,1\} \end{gathered}$$

2.1.2 松弛线性规划

2.1.2.1 概念

将去掉整数约束的整数规划问题成为整数规划的松弛线性规划

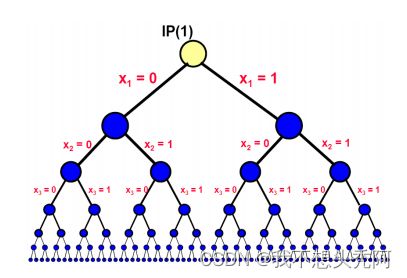
2.1.2.2 例题

整数规划问题：
$$\begin{gathered} IP(1) \\ max10x_1+4x_2+9x_3 \\ 5x_1+4x_2+3x_3\le 9 \\ 0\le x_i\le 1,x_i\in \mathbf{Z},1\le i\le 3 \end{gathered}$$
该整数规划的松弛线性规划为：
$$\begin{gathered} IP(1) \\ max10x_1+4x_2+9x_3 \\ 5x_1+4x_2+3x_3\le 9 \\ 0\le x_i\le 1,1\le i\le 3 \end{gathered}$$

2.2 单纯形算法

单纯形算法是求解线性规划的经典方法。它的执行时间在最坏情况下不是多项式的，但是在实际中此算法通常相当快速。

2.2.1 主要思想

• 每轮迭代都关联一个“基本解”，容易从松弛型中计算得到。
• 每轮迭代把一个松弛型转换成一个等价的松弛型。
• 最终，指导一个最优解变得“明显”

2.3 分支定界算法

2.3.1 枚举树

2.3.1.1 概念

枚举树是以树状结构将可行域不断进行划分并一一列举出来的数据结构。

2.3.2 分支定界算法

2.3.2.1 剪枝规则

分支定界算法是为了对上述的枚举树进行剪枝，剪枝规则如下：

• 若已找到某个节点的最优解，删除其所有子孙节点；
• 若已知枚举树中某个节点的最优解，而当前节点的松弛线性规划问题的最优解都比这个解要小，则删除当前节点及其子孙节点；
• 若当前节点对应的松弛线性规划问题没有可行解，删除当前节点及其子孙节点。

2.3.2.2 算法

三、集合覆盖

3.1 问题定义

3.1.1 覆盖

设$A$是非空集合，$C$是集合$A$的非空子集组成的集合，即$C=\{A_{\alpha }|A_{\alpha }\subset A,A_{\alpha }\ne \varnothing \}$，$C$是集合$A$的覆盖，若$C$满足
$${\cup }_{A_{\alpha }\in C}{A}_{\alpha }=A$$

3.1.2 最小全覆盖问题

令$U$为一有限集，$S=\{s_1,s_2,...,s_n\}$为由$U$的$n$个子集构成的集族，全覆盖问题是找到$S$最小的自己覆盖集合$U$。

3.1.3 最大子覆盖问题

令$U$为一有限集，$S=\{s_1,s_2,...,s_n\}$为由$U$的$n$个子集构成的集族，给定正整数$k$，最大子覆盖问题是从$S$中找到$k$个子集，使得这$k$个子集覆盖集合$U$中最多的元素。

3.2 爬山算法

3.2.1 概念

爬山算法（hill-climbing algorithm）是一个解决子模优化问题的局部搜索算法。算法12.1是爬山算法的一个实例，它解决了最大子覆盖问题。

四、模块度及社区发现

4.1 模块度

4.1.1 概念

社区划分的好坏与划分后的社区内部顶点及社区之间顶点的连接程度紧密相关，划分越好的社区中各社区内部顶点之间连接得也越紧密，而社区之间连接得越稀疏。模块度正是基于这样的一个观测而定义的。

4.1.2 无向图的模块度定义

4.1.2.1 表达式

无向图的模块度可以计算为:
$$Q=\frac{1}{2m}\sum _{i,j}(A_{ij}-\frac{k_i{k}_j}{2m})\delta (C_i,C_j)$$

• $n$：顶点个数
• $m$：边数
• $A$：邻接矩阵
• $k_i$：顶点$v_i$的度
• $\delta (C_i,C_j)=\{\begin{array}{rl}1,如果v_i和v_j属于同一个社区& \\ 0,& 否则\end{array}$

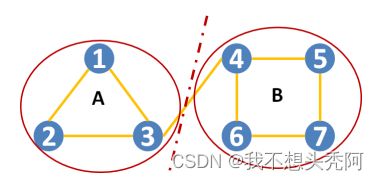
4.1.2.2 例题

解：由图可知，$m=8,k_1=2,k_2=2,k_3=3,k_4=3,k_5=2,k_6=2,k_7=2$。
$$\begin{gathered} Q=\frac{1}{16}[(A_{11}-\frac{k_1{k}_1}{16})+2(A_{12}-\frac{k_1{k}_2}{16})+2(A_{13}-\frac{k_1{k}_3}{16}) \\ +(A_{22}-\frac{k_2{k}_2}{16})+2(A_{23}-\frac{k_2{k}_3}{16})+ \\ (A_{33}-\frac{k_3{k}_3}{16}) \\ +(A_{44}-\frac{k_4{k}_4}{16})+2(A_{45}-\frac{k_4{k}_5}{16})+2(A_{46}-\frac{k_4{k}_6}{16})+2(A_{47}-\frac{k_4{k}_7}{16}) \\ +(A_{55}-\frac{k_5{k}_5}{16})+2(A_{56}-\frac{k_5{k}_6}{16})+2(A_{57}-\frac{k_5{k}_7}{16}) \\ +(A_{66}-\frac{k_6{k}_6}{16})+2(A_{67}-\frac{k_6{k}_7}{16}) \\ +(A_{77}-\frac{k_7{k}_7}{16})]=\frac{47}{128} \end{gathered}$$

4.1.2.3 另一种模块度表达式

$$\begin{gathered} Q=\frac{1}{2m}\sum _{i,j}(A_{ij}-\frac{k_i{k}_j}{2m})\delta (C_i,C_j) \\ =\sum _{i,j}(\frac{A_{ij}}{2m}-\frac{k_i{k}_j}{4m^2})\delta (C_i,C_j) \\ =(\sum _{i,j}\frac{A_{ij}}{2m}-\frac{{\sum }_i{k}_i{\sum }_j{k}_j}{4m^2})\delta (C_i,C_j) \\ =\sum _{c\in C}[\frac{{\sum }_{in}^c}{2m}-(\frac{{\sum }_{tot}^c}{2m}{)}^2] \end{gathered}$$

• ${\sum }_{in}^c$：社区$c$内部有向边的数量；
• ${\sum }_{tot}^c$：社区$c$内部所有顶点度的总和；

4.1.2.4 例题

用上述表达式计算上图的模块度：
$$Q=[\frac{6}{16}-(\frac{7}{16}{)}^2]+[\frac{8}{16}-(\frac{9}{16}{)}^2]=\frac{47}{128}$$

4.1.3 权重无向图的模块度定义

4.1.3.1 表达式

假设$W$为图$G$的权重矩阵，其中
$$W_{ij}=\{\begin{array}{r}{w}_{ij},如果A_{ij}=1\\ 0,否则\end{array}$$
即图$G$的每条边上赋予了一个权重$w_{ij}$。权重无向图的模块度定义为：
$$Q=\frac{1}{2m}\sum _{i,j}(W_{ij}-\frac{k_i{k}_j}{2m})\delta (C_i,C_j)$$

• $2m={\sum }_{i,j}{W}_{ij}$
• $k_i={\sum }_j{W}_{ij}$

4.1.4 有向图的模块度定义

4.1.4.1 表达式

假设$A$为有向图$G$的邻接矩阵，其中$m$为有向边的数量，定义顶点$v_i$的出度和入度分别为：
$$k_i^{out}=\sum _j{A}_{ij}和k_i^{in}=\sum _j{A}_{ji}$$
有向图的模块度定义如下
$$Q=\frac{1}{m}\sum _{i,j}(A_{ij}-\frac{k_i^{out}{k}_j^{in}}{m})\delta (C_i,C_j)$$

4.1.5 模块度的矩阵定义

4.1.5.1 表达式

定义一个$n\times k$的矩阵$S$，$S_{ij}=1$表示顶点$v_i$属于第$j$个社区，$S_{ij}=0$表示顶点$v_i$不属于第$j$个社区，所以
$$\delta (C_i,C_j)=\sum _r{S}_{ir}{S}_{jr}$$
定义实对称矩阵$B$，其元素满足
$$B_{ij}=A_{ij}-\frac{k_i{k}_j}{2m}$$
则社区结构模块度可以改写为：
$$\begin{gathered} Q=\frac{1}{2m}\sum _{i,j}(A_{ij}-\frac{k_i{k}_j}{2m})\delta (C_i,C_j) \\ =\frac{1}{2m}\sum _{i,j}{B}_{ij}\sum _r{S}_{ir}{S}_{jr} \\ =\frac{1}{2m}\sum _{i,j}\sum _r{B}_{ij}{S}_{ir}{S}_{jr} \\ =\frac{1}{2m}Tr(S^{T}BS) \end{gathered}$$
其中$Tr(S^{T}BS)$为矩阵的迹，即对角元素之和。

4.2 Louvain算法

4.2.1 算法步骤

4.2.2 表达式

模块度增益$\Delta Q(v_i\to B)$计算为
KaTeX parse error: Can't use function '$' in math mode at position 2: $̲\Delta Q(v_i\ri…
模块度损失$\Delta Q(A\to v_i)$计算为
$$\Delta Q(A\to v_i)=\frac{{\sum }_{i,tot}^{A^{\prime }}\cdot k_i}{2m^2}-\frac{k_{i,in}^{A^{\prime }}}{2m}$$