计算机视觉中的深度学习：卷积神经网络介绍

在本文中，我们会学习卷积神经网络，一种在计算机视觉中常用的深度学习模型，你将会学着将它们运用到分类问题中。
我们首先会介绍卷积神经网络背后的一些理论，特别的：

• 什么是卷积和最大池化?

• 什么是卷积网络？

• 卷积网络学到了什么东西？

接下来我们会用小的数据集来概括图像分类问题：

• 从零开始训练你的小卷积网络

• 使用数据增加来避免过拟合

• 使用预训练的卷积网络来做特征提取

• 对预训练卷积网络调参

最后我们会概括几个可视化的技术来学习如何分类。

接下来是我们的第一节，卷积神经网路的介绍

我们潜入卷积神经网络的理论，并探寻为什么它在计算机视觉任务中那么成功。首先，我们实际看看一个简单的卷积网络的例子。我们将会用卷积网络来分类MNIST数字，在之前我们以及用全连接做到了97.8%的识别率。尽管我们的卷积网络很基础，但是其正确率和原来的全连接比，照样完胜。
接下来6行代码将会给你展示最基础的卷积网络长什么样，其实就是一些二维卷积和二维最大池化层的堆叠。我们接下来将会看看他们到底具体做了些什么，一个卷积拿进去的张量的形状：（长，宽，通道数）不包括批次的维数。在我们的例子中，我们将会处理输入形状为(28,28,1)的数据，这就是MNIST中数据的格式。

from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))

接下来让我们看看卷积网络的结构：

>>> model.summary()
________________________________________________________________
Layer (type) Output Shape Param #
================================================================
conv2d_1 (Conv2D) (None, 26, 26, 32) 320
________________________________________________________________
maxpooling2d_1 (MaxPooling2D) (None, 13, 13, 32) 0
________________________________________________________________
conv2d_2 (Conv2D) (None, 11, 11, 64) 18496
________________________________________________________________
maxpooling2d_2 (MaxPooling2D) (None, 5, 5, 64) 0
________________________________________________________________
conv2d_3 (Conv2D) (None, 3, 3, 64) 36928
================================================================
Total params: 55,744
Trainable params: 55,744
Non-trainable params: 0

 我们可以看到每一个卷积层和池化层的输出都是三维的张量。宽度和高度随着网络的加深开始收缩。通道的数量由卷积层受到的第一个参数来控制。
接下来就是将我们的输出张量喂进全连接分类网络。分类器处理的是一维向量，而我们的输出是一个三维的张量，所以我们需要把我们的三维输出压成一维的，接下来，我们加一层密度层：

model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))

我们接下来要做一个10分类，我们选用了softmax作为激活函数，输出维度为10，我们的网络现在长成这个样子：

>>> model.summary()
Layer (type) Output Shape Param #
================================================================
conv2d_1 (Conv2D) (None, 26, 26, 32) 320
________________________________________________________________
maxpooling2d_1 (MaxPooling2D) (None, 13, 13, 32) 0
________________________________________________________________
conv2d_2 (Conv2D) (None, 11, 11, 64) 18496
________________________________________________________________
maxpooling2d_2 (MaxPooling2D) (None, 5, 5, 64) 0
________________________________________________________________
conv2d_3 (Conv2D) (None, 3, 3, 64) 36928
________________________________________________________________
flatten_1 (Flatten) (None, 576) 0
________________________________________________________________
dense_1 (Dense) (None, 64) 36928
________________________________________________________________
dense_2 (Dense) (None, 10) 650
================================================================
Total params: 93,322
Trainable params: 93,322
Non-trainable params: 0

最后我们将使用之前使用过的代码来训练：

from keras.datasets import mnist
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
model.compile(optimizer='rmsprop',
 loss='categorical_crossentropy',
 metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=64)

然后评测一下最终结果

>>> test_loss, test_acc = model.evaluate(test_images, test_labels)
>>> test_acc
0.99080000000000001

为什么一个简单的卷积神经网络能够比全连接模型效果好那么多呢，我们需要继续潜入卷积层和最大池化层来理解这个事情。

卷积算子

全连接层学习全局图案，而卷积层则学习局部的图案

 

这个关键的特征给了卷积网络两个有意思的特性：

在keras的卷积层中，第一个传入的参数就是Conv2D(output_depth, (window_height, window_width))。
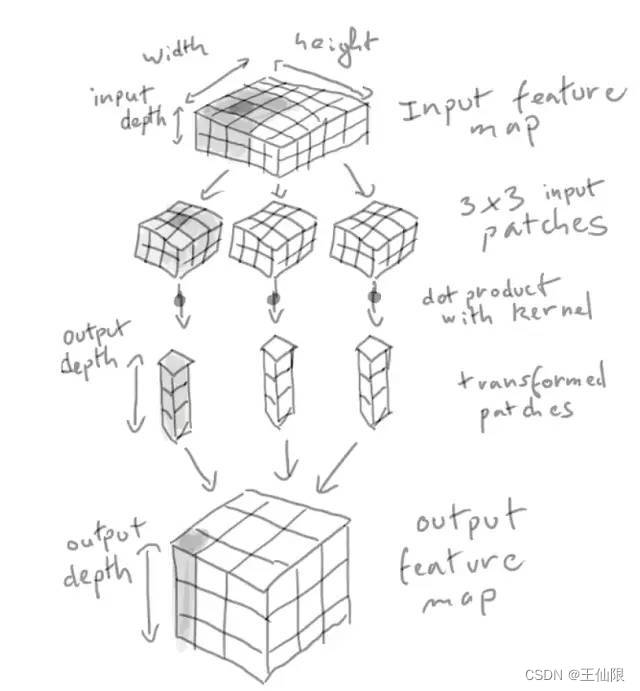
一个卷积通过滑动来工作，在每个可能的位置停止，并从周围的特征里面提取三维补丁。
示意图如下：

 

• 学习到的图案具有平移不变性，在全连接中学到的图案和位置有关，而卷积网络则有更高的数据效率。

• 能学习图案的空间层次，如下图，第一层学习小的局部图案例如边缘，但第二个卷积层将会基于第一层学习更大的特征。这将使得卷积网络更加有效的学习到进一步抽象复杂的特征。

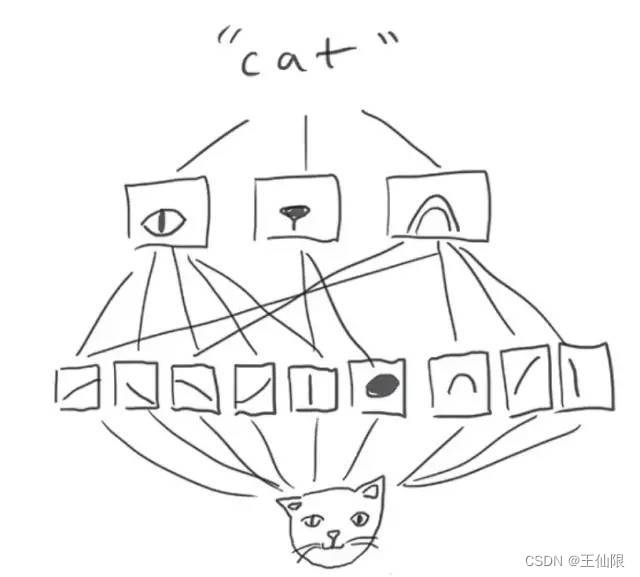
  在三维张量的卷积运算称为“特征图”，有两个空间坐标（宽和高），和一个深度坐标（也称作通道数）对于RGB图像来说，深度坐标的维度就是3。对于MNIST来说，黑白图深度就是1。卷积算子从输入特征图提取补丁，并对所有的补丁做某些变换，然后产生我们的输出特征图。输出特征图仍然是三维张量，不过这里的深度不再代表什么具体的颜色了，而是我们叫做滤波器的东西。滤波器对输入数据的某一特定方面进行编码，在高层次，一个简单的滤波器能编码输入中一个面的存在。
  卷积由以下两个关键参数所定义：

• 从输入中提取的补丁块的大小。

• 输出特征映射的深度，即滤波器的数量。在我们的例子中，我们从深度为32开始，深度为64结束。

注意到我们得到的输出的宽度和高度或许和输入的宽度和高度不一样，这里有两个原因：

边框影响，由于输入特征映射填充造成的。

滑动的使用，我们稍后会定义。

让我们来看一下这些注意点。

理解边框效应和填充
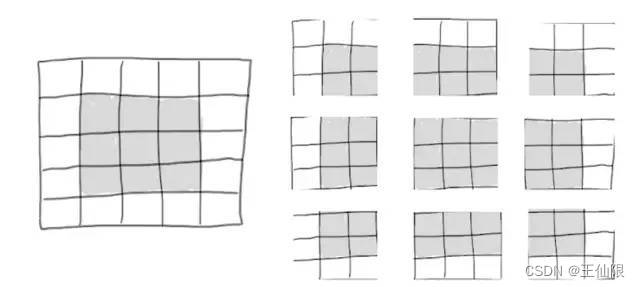
考虑一个5x5的特征映射，共25个小块。但那时只有9个不同的小块，也就说你可以注意力放在3x3的小窗上。因此输出的特征映射将会是3x3的:这缩小了很多，在每个维度上缩小了两个小块，你将会在之前的例子中看到”边界效应”。

如果你想要得到一个和原来的输入有相同的输出特征映射，你可以选择使用填充。填充通过增加合适数量的行列向量，对于
                                                                                 3x3
的窗，可以选择在左右侧各加一列，上下各加一行。对于
                                                                                 5X5
的窗口，就是两行了。 

在卷积层中，填充可以通过“填充”参数来配置，“填充”参数中包含两个值："valid"和"same"，前者意味着不填充，后者意味着让输入输出有相同的宽高，而padding参数的默认值是"valid"。

理解卷积滑动

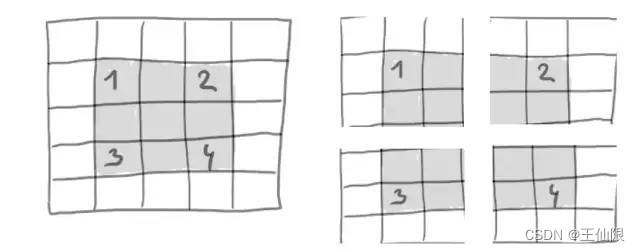
另一个影响输出大小的是"stride"。在我们目前为止对于卷积的描述，我们假设卷积窗口的中心块都配置好了。然而，两个连续的窗口之间实际上有一个卷积的参数，叫做"stride"，默认值为1。在接下来这幅图你可以看到stride设为2的情况。

使用stride为2，意味着宽和高都通过因子2来下采样。滑动卷积在实际中很少使用，尽管他们能在很多种模型中派上用场，熟悉这块内容总是好的。
为了对特征进行下采样，除了滑动，还可以通过最大池化算子来做到。

最大池化算子

在我们的卷积例子里面，你已经注意到特征映射的数量在经过最大池化以后会减半，就像滑动卷积一样，对于降采样非常的积极。
最大池化由从输入特征来提取窗口以及输出每个通道的最大值。这就和卷积很相似了。
我们为什么要做池化呢？如果把池化这一步去掉会发生什么呢？

model_no_max_pool = models.Sequential()
model_no_max_pool.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))
model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))

输出结构：

>>> model_no_max_pool.summary()
Layer (type) Output Shape Param #
================================================================
conv2d_4 (Conv2D) (None, 26, 26, 32) 320
________________________________________________________________
conv2d_5 (Conv2D) (None, 24, 24, 64) 18496
________________________________________________________________
conv2d_6 (Conv2D) (None, 22, 22, 64) 36928
================================================================
Total params: 55,744
Trainable params: 55,744
Non-trainable params: 0

 这么设置有什么错吗 ? 有两点：
1.这不有利于学习空间层次的特征。3 x 3的窗口在第3层将只包含输入中 7x 7的信息。卷积网络能够学习到的高级特征还是太小。我们需要最后一层卷积层能够包含全部输入的信息。
2.最终的特征的系数太多了。

简短的说，使用下采样是为了减少特征系数的数量，同时让连续的卷积层去处理更大的窗口以减少空间滤波器数量。
注意最大池化不是唯一可以取得下采样的方法。你也知道stride也可以，你还可以伸用平均池化。然而最大池化往往比这些替代方法表现得好。