【论文笔记】KGAT: Knowledge Graph Attention Network for Recommendation
原文作者:Xiang Wang,Xiangnan He,Yixin Cao,Meng Liu,Tat-Seng Chua
原文标题:KGAT: Knowledge Graph Attention Network for Recommendation
原文来源:KDD 2019
原文链接:https://arxiv.org/abs/1905.07854
本文提出了一种新的推荐方法KGAT,能够根据实体间的高阶关系特征建模,并具有一定的可解释性。以端到端方式对KG的高阶连通性进行了显式建模。递归地从节点的邻居(可以是用户、项目或属性)传播嵌入,并使用注意机制来区分邻居的重要性。
KGAT: Knowledge Graph Attention Network for Recommendation
问题定义
1)Collaborative Knowledge Graph(CKG)
作者首先建立一个item-entity对齐集合 A = { ( i , e ) ∣ i ∈ I , e ∈ E } \mathcal{A = \{(}i,e) \mid i \in I,e\mathcal{\in E\}} A={(i,e)∣i∈I,e∈E},其中 ( i , e ) (i,e) (i,e)表示item在KG中与一个实体对齐。CKG将用户行为和item知识编码为统一的关系图谱。用户行为表示为三元组 ( u , Interact , i ) \left( u,\text{Interact},i \right) (u,Interact,i), y ui = 1 y_{\text{ui}} = 1 yui=1表示用户和item之间有一个额外的关系 Interact \text{Interact} Interact。那么整个知识图谱为: G = { ( h , r , t ) ∣ h , t ∈ E ′ , r ∈ R ′ } , E ′ = E ∪ U , R ′ = R ∪ Interact \mathcal{G =}\left\{ \left( h,r,t \right) \mid h,t \in \mathcal{E}^{'},r \in \right.\ \left. \ \mathcal{R}^{'} \right\},\mathcal{E}^{'}\mathcal{= E \cup U},\mathcal{R}^{'}\mathcal{= R \cup}\text{Interact} G={(h,r,t)∣h,t∈E′,r∈ R′},E′=E∪U,R′=R∪Interact。
2)任务描述
输入CKG,包括user-item二分图,知识图谱。
输出能够预测用户u与item i交互的概率 y ^ ui {\widehat{y}}_{\text{ui}} y ui的预测函数。
3)高阶连通性
作者认为探索高阶连通性对于高质量的推荐是必不可少的。节点间的高阶连通性定义为多跳的关系路径: e 0 ⟶ r 1 e 1 ⟶ r 2 ⋯ ⟶ r L e L e_{0}\overset{r_{1}}{\longrightarrow}e_{1}\overset{r_{2}}{\longrightarrow}\cdots\overset{r_{L}}{\longrightarrow}e_{L} e0⟶r1e1⟶r2⋯⟶rLeL。 ( e l − 1 , r l , e l ) \left( e_{l - 1},r_{l},e_{l} \right) (el−1,rl,el)是第 l l l个三元组,L是序列长度。类似于协同过滤和监督学习方法都没有充分探索高阶连通性。
模型架构
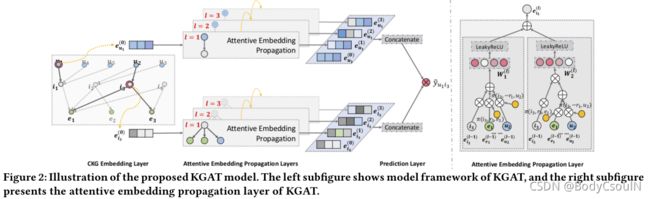
如图2所示,整个模型有三个主要部分:
-
嵌入层。在保持CKG的结构下,将每个节点表示为一个向量。
-
注意力嵌入传播层。递归传播嵌入给邻居,以此更新节点的表示。并使用知识感知注意力机制学习每个邻居的权重。
-
预测层。将user和item的表示聚合,并输出预测分数。
embedding layer
使用TransR模型嵌入知识图谱:
g ( h , r , t ) = ∥ W r e h + e r − W r e t ∥ 2 2 g(h,r,t) = \left. \parallel\mathbf{W}_{r}\mathbf{e}_{h} + \mathbf{e}_{r} - \mathbf{W}_{r}\mathbf{e}_{t} \right.\parallel_{2}^{2} g(h,r,t)=∥Wreh+er−Wret∥22
注意力嵌入传播层
每一个注意力层分为三个部分:信息传播、注意力、信息聚合。
信息传播:由于实体可能在不同的三元组中,可以作为桥梁将三元组连接并传播信息。对于实体h,其自我网络(ego-network)表示为 N h = { ( h , r , t ) ∣ ( h , r , t ) ∈ G } \mathcal{N}_{h} = \{(h,r,t) \mid (h,r,t) \in \mathcal{G\}} Nh={(h,r,t)∣(h,r,t)∈G}。计算h的自我网络的线性组合:
e N h = ∑ ( h , r , t ) ∈ N h π ( h , r , t ) e t \mathbf{e}_{\mathcal{N}_{h}} = \sum_{(h,r,t) \in \mathcal{N}_{h}}^{}\pi(h,r,t)\mathbf{e}_{t} eNh=(h,r,t)∈Nh∑π(h,r,t)et
这一步是传递所有以h为头的三元组的尾实体的信息。表示了在关系r下,有多少信息从t传播到h(h是网络的中心)。
注意力:使用注意力机制计算 π ( h , r , t ) \pi(h,r,t) π(h,r,t)。注意力得分取决于在关系空间中头实体与尾实体之间的距离,也就是说距离更近的实体传播更多的信息。
π ( h , r , t ) = ( W r e t ) ⊤ tanh ( ( W r e h + e r ) ) \pi(h,r,t) = \left( \mathbf{W}_{r}\mathbf{e}_{t} \right)^{\top}\tanh\left( \left( \mathbf{W}_{r}\mathbf{e}_{h} + \mathbf{e}_{r} \right) \right) π(h,r,t)=(Wret)⊤tanh((Wreh+er))
这里基于TransR,如果三元组关系能满足 e h r + e r ≈ e t r \mathbf{e}_{h}^{r} + \mathbf{e}_{r} \approx \mathbf{e}_{t}^{r} ehr+er≈etr,那么 ( W r e h + e r ) \left( \mathbf{W}_{r}\mathbf{e}_{h} + \mathbf{e}_{r} \right) (Wreh+er)和 ( W r e t ) ⊤ \left( \mathbf{W}_{r}\mathbf{e}_{t} \right)^{\top} (Wret)⊤的相似度越高,内积越大,则权重越大。
然后使用softmax函数进行归一化。最终的注意力分数表明哪个邻居节点应该给予更多的注意力。
信息聚合:将实体的表示和其自我网络的表示聚合为一个新向量 e h ( 1 ) = f ( e h , e N h ) \mathbf{e}_{h}^{(1)} = f\left( \mathbf{e}_{h},\mathbf{e}_{\mathcal{N}_{h}} \right) eh(1)=f(eh,eNh)。有三种方式实现:GCN Aggregator、GraphSage Aggregator、Bi-Interaction。
类似于multi-head,通过增加层数探索高阶连通信息。重复上述三个步骤多次,当前第 l l l次有:
e h ( l ) = f ( e h ( l − 1 ) , e N h ( l − 1 ) ) , e h ( l − 1 ) = ∑ ( h , r , t ) ∈ N h π ( h , r , t ) e t ( l − 1 ) e_{h}^{(l)} = f\left( e_{h}^{(l - 1)},e_{N_{h}}^{(l - 1)} \right),e_{h}^{(l - 1)} = \sum_{(h,r,t) \in N_{h}}^{}\pi(h,r,t)e_{t}^{(l - 1)} eh(l)=f(eh(l−1),eNh(l−1)),eh(l−1)=(h,r,t)∈Nh∑π(h,r,t)et(l−1)
模型预测层
经过上述两层,得到了用户u和item i的多个表示: { e u ( 1 ) , ⋯ , e u ( L ) } \left\{ \mathbf{e}_{u}^{(1)},\cdots,\mathbf{e}_{u}^{(L)} \right\} {eu(1),⋯,eu(L)}, { e i ( 1 ) , ⋯ , e i ( L ) } \left\{ \mathbf{e}_{i}^{(1)},\cdots,\mathbf{e}_{i}^{(L)} \right\} {ei(1),⋯,ei(L)}。不同层的输出强调不同阶的连通性信息。然后将u和i的向量拼接起来:
e u ∗ = e u ( 0 ) ∥ ⋯ ∥ e u ( L ) , e i ∗ = e i ( 0 ) ∥ ⋯ ∥ e i ( L ) e_{u}^{*} = e_{u}^{(0)} \parallel \cdots \parallel e_{u}^{(L)},e_{i}^{*} = e_{i}^{(0)} \parallel \cdots \parallel e_{i}^{(L)} eu∗=eu(0)∥⋯∥eu(L),ei∗=ei(0)∥⋯∥ei(L)
通过执行嵌入传播操作来丰富初始嵌入,还可以通过调整l来控制传播的强度。最终的预测得分:
y ^ ( u , i ) = e u ∗ ⊤ e i ∗ \widehat{y}(u,i) = \mathbf{e}_{u}^{*\top}\mathbf{e}_{i}^{*} y (u,i)=eu∗⊤ei∗
训练
损失函数为CF对应pair-wise的loss+图谱loss+参数正则loss。
L KGAT = L KG + L CF + λ ∥ Θ ∥ 2 2 \mathcal{L}_{\text{KGAT}} = \mathcal{L}_{\text{KG}} + \mathcal{L}_{\text{CF}} + \lambda \parallel \Theta \parallel_{2}^{2} LKGAT=LKG+LCF+λ∥Θ∥22
使用mini-batch Adam交替训练 L KG \mathcal{L}_{\text{KG}} LKG与 L CF \mathcal{L}_{\text{CF}} LCF。
实验
选择的数据集有:Amazon-book、Last-FM、Yelp2018。其主要信息如下表所示。
实验结果如表二所示。
KGAT在所有数据集上性能表现都是最优的。KGAT通过叠加多个注意力嵌入传播层,能够显式地探索高阶连通性,从而有效地捕获协同信号。验证了捕获协同信号对知识传递的意义。
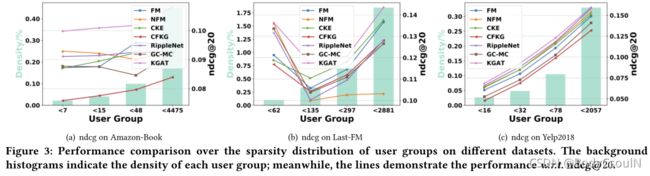
作者还进行了关于稀疏交互的实验,研究连通性信息能否缓解稀疏问题。结果如图3所示。
可以看到,KGAT在绝大多数情况下,表现都比其他模型要好。尤其是在Amazon-Book和Yelp2018两个最稀疏的用户群体上。再次验证了高阶连通性建模的重要性。而在一些比较稠密的交互数据上,KGAT可能表现稍差一点,原因是稠密的交互数据中会有一些用户偏好noise。
对模型深度的研究发现,在三层注意力传播嵌入层时模型效果更好,说明实体之间的三阶关系就足以捕获协作信号。
对于KGE和Attention的影响,作者发现attention比KGE更有效,原因可能是KGE对所有邻居实体一视同仁,可能产生noises。
另外连通性路径也为推荐的可解释性提供了很好的证据。
总结
这篇文章将注意力机制引入推荐系统。基于TransR模型,先将知识图谱嵌入,得到实体和关系的向量表示;然后对所有头实体,利用注意力机制,计算邻居实体(三元组中的尾实体)传播给该实体的信息量,注意力得分越高,则传播的信息就越多,在使用聚合器将实体嵌入向量和其他实体传递给该实体的信息聚合,得到某阶下实体的丰富表示(这里的阶应该是图谱中的跳数)。
最后,将各层得到的向量拼接起来,使用内积得到user和item交互的评分。
关于论文第五页的高阶连通性 暂时不理解。参考:
https://github.com/xiangwang1223/knowledge_graph_attention_network/issues/2
这篇文章的缺点?不足?