DIDL笔记(pytorch版本)(三)
文章目录
-
- 拟合问题
- 权重衰减
- 丢弃法
拟合问题
在训练数据集大小一定的情况下,模型越简单,但是数据复杂。训练初期误差下降后,后面难以继续降低,即使在最后一次结束,训练误差还是很高。
训练数据集过少,甚至少于模型参数数量时,这样会显得模型过于复杂,容易被训练数据中的噪声影响。即使经过迭代训练误差下降,但是在测试数据集上误差很高。
欠拟合指模型无法得到较低的训练误差,过拟合指模型的训练误差远小于它在测试数据集上的误差。
import torch
import numpy as np
import d2l
n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = torch.randn((n_train + n_test, 1))
poly_features = torch.cat((features, torch.pow(features, 2), torch.pow(features, 3)), 1)
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
+ true_w[2] * poly_features[:, 2] + true_b)
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
num_epochs, loss = 100, torch.nn.MSELoss()
def fit(train_features, test_features, train_labels, test_labels):
net = torch.nn.Linear(train_features.shape[-1], 1)
# 通过Linear文档可知,pytorch已经将参数初始化了,所以我们这里就不手动初始化了
batch_size = min(10, train_labels.shape[0])
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
l = loss(net(X), y.view(-1, 1))
optimizer.zero_grad()
l.backward()
optimizer.step()
train_labels = train_labels.view(-1, 1)
test_labels = test_labels.view(-1, 1)
train_ls.append(loss(net(train_features), train_labels).item())
test_ls.append(loss(net(test_features), test_labels).item())
print('final epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])
print('weight:', net.weight.data,
'\nbias:', net.bias.data)
fit(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:])
fit(features[:n_train, :], features[n_train:, :], labels[:n_train],
labels[n_train:])
权重衰减
权重衰减 = 正则化;正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小。为什么呢?
![]()
首先损失函数是希望小的并且上式两项都是大于0,所以每一项都会去趋近于0。当设置 λ > 0 \lambda>0 λ>0,那么在损失函数变小的过程中,正则项也会变少。正则项时所有权重的平方和,所以也就是说每个权重在减少。
import torch
import torch.nn as nn
import numpy as np
import d2l
n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05
features = torch.randn((n_train + n_test, num_inputs))
labels = torch.matmul(features, true_w) + true_b # matmul 矩阵乘法
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]
def init_params():
w = torch.randn((num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
def l2_penalty(w):
return (w**2).sum() / 2
batch_size, num_epochs, lr = 1, 100, 0.003
net, loss = d2l.linreg, d2l.squared_loss
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
# 原始形式
def fit(lambd):
w, b = init_params()
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
# 添加了L2范数惩罚项
l = loss(net(X, w, b), y) + lambd * l2_penalty(w)
l = l.sum()
if w.grad is not None:
w.grad.data.zero_()
b.grad.data.zero_()
l.backward() # 计算梯度
d2l.sgd([w, b], lr, batch_size) # 参数迭代
train_ls.append(loss(net(train_features, w, b), train_labels).mean().item())
test_ls.append(loss(net(test_features, w, b), test_labels).mean().item())
print('L2 norm of w:', w.norm().item())
fit(lambd=0)
fit(lambd=3)
# 简洁形式
def fit_pytorch(wd):
# 对权重参数衰减。权重名称一般是以weight结尾
net = nn.Linear(num_inputs, 1)
nn.init.normal_(net.weight, mean=0, std=1)
nn.init.normal_(net.bias, mean=0, std=1)
optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # 对权重参数衰减
optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr) # 不对偏差参数衰减
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
l = loss(net(X), y).mean()
optimizer_w.zero_grad()
optimizer_b.zero_grad()
l.backward()
# 对两个optimizer实例分别调用step函数,从而分别更新权重和偏差
optimizer_w.step()
optimizer_b.step()
train_ls.append(loss(net(train_features), train_labels).mean().item())
test_ls.append(loss(net(test_features), test_labels).mean().item())
print('L2 norm of w:', net.weight.data.norm().item())
fit_pytorch(0)
fit_pytorch(3)
丢弃法
深度学习常用丢弃法来解决过拟合问题。在多层神经网络中,隐藏层的隐藏单元 h i h_i hi会有 p p p的概率丢弃。这时的 h i h_i hi为: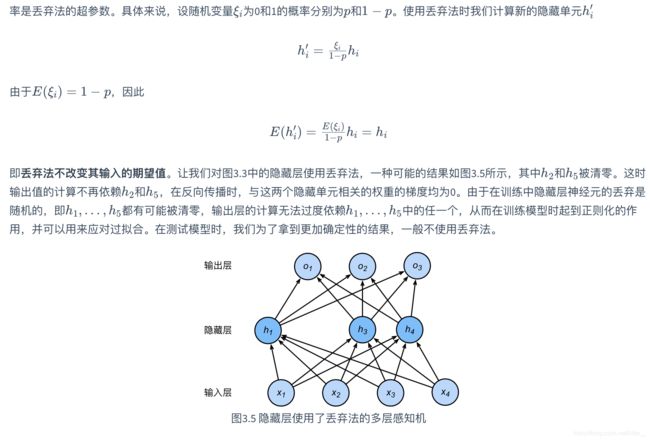
# 在多层感知机原始代码的基础上,部分代码改变
# 原始形式
def dropout(X, drop_prob):
X = X.float()
assert 0 <= drop_prob <= 1
keep_prob = 1 - drop_prob
# 这种情况下把全部元素都丢弃
if keep_prob == 0:
return torch.zeros_like(X)
mask = (torch.rand(X.shape) < keep_prob).float() # mask 要么为0,要么为1, 随机选取了
return mask * X / keep_prob
def net(X, is_training=True):
X = X.view(-1, num_inputs) # 行向量
H1 = (torch.matmul(X, W1) + b1).relu()
if is_training: # 只在训练模型时使用丢弃法
H1 = dropout(H1, drop_prob1) # 在第一层全连接后添加丢弃层
H2 = (torch.matmul(H1, W2) + b2).relu()
if is_training:
H2 = dropout(H2, drop_prob2) # 在第二层全连接后添加丢弃层
return torch.matmul(H2, W3) + b3
# 在多层感知机简洁代码的基础上,部分代码改变
# 简洁形式
net = nn.Sequential(
d2l.FlattenLayer(), # 形状转换
nn.Linear(num_inputs, num_hiddens1),
nn.ReLU(),
nn.Dropout(drop_prob1),
nn.Linear(num_hiddens1, num_hiddens2),
nn.ReLU(),
nn.Dropout(drop_prob2),
nn.Linear(num_hiddens2, 10)
)