机器学习 之 贝叶斯估计与范数

贝叶斯估计才是完全体，我一直不倾向于叫它贝叶斯，就叫条件概率估计好了。
贝叶斯估计分为共轭的和不共轭的，共轭的可以直接求出来，但是不共轭的需要估计。

先说共轭的(高斯)：
$$\begin{gathered} p(w|\text{t},\text{X},{\delta }^2)\simeq p(\text{t}|w,\text{X},{\delta }^2)p(w|{\mu }_0,{\Sigma }_0) \\ =(\frac{1}{\sqrt{2\pi }\delta }{)}^n{e}^{-\frac{(\text{t}-\text{X}\text{w}{)}^T(\text{t}-\text{X}\text{w})}{2{\delta }^2\text{I}}}\times (\frac{1}{\sqrt{2\pi {\Sigma }_0}}{)}^n{e}^{-\frac{(\text{w}-{\mu }_0{)}^T(\text{w}-{\mu }_0)}{2{\Sigma }_0}} \\ \simeq e^{-\frac{1}{2}(\frac{(\text{t}-\text{X}\text{w}{)}^T(\text{t}-\text{X}\text{w})}{{\delta }^2\text{I}}+\frac{(\text{w}-{\mu }_0{)}^T(\text{w}-{\mu }_0)}{{\Sigma }_0})} \\ \simeq e^{-\frac{1}{2}(\frac{-2{\text{t}}^T\text{X}\text{w}+{\text{w}}^T{\text{X}}^T\text{X}\text{w}}{{\delta }^2\text{I}}+\frac{{\text{w}}^T\text{w}-2{\mu }_0^T\text{w}}{{\Sigma }_0})} \end{gathered}$$

注意这里的${\mu }_0,{\Sigma }_0$是$w$的高斯分布的均值，方差(本来是标准的，但现在是我们设定的)。消除了很多，因为后面一一对应时没用。由于我们认定后验概率是高斯分布，因此后验概率应该为
$$\begin{gathered} p(\text{w}|\text{t},\text{X},{\delta }^2)=N({\mu }_w,{\Sigma }_w) \\ \simeq e^{-\frac{(\text{w}-{\mu }_w{)}^T(\text{w}-{\mu }_w)}{2{\Sigma }_w}} \\ \simeq e^{-\frac{{\text{w}}^T\text{w}-2{\mu }_w^T\text{w}}{2{\Sigma }_w}} \end{gathered}$$

这里面有一个线性二次项，一个线性一次项，对应相等，从而有
$$\begin{gathered} \frac{{\text{w}}^T\text{w}}{{\Sigma }_w}=\frac{{\text{w}}^T{\text{X}}^T\text{X}\text{w}}{{\delta }^2\text{I}}+\frac{{\text{w}}^T\text{w}}{{\Sigma }_0} \\ ={\text{w}}^T(\frac{{\text{X}}^T\text{X}}{{\delta }^2\text{I}}+\frac{1}{{\Sigma }_0})\text{w} \\ \frac{1}{{\Sigma }_w}=\frac{{\text{X}}^T\text{X}}{{\delta }^2\text{I}}+\frac{1}{{\Sigma }_0} \\ {\Sigma }_w=(\frac{1}{{\delta }^2}{\text{X}}^T\text{X}+{\Sigma }_0^{-1}{)}^{-1} \end{gathered}$$

同样的，将线性一次项相等，会获得${\mu }_w$，这样$w$的方差，均值都获得了
$$\begin{gathered} \frac{-2{\mu }_w^T\text{w}}{{\Sigma }_w}=\frac{-2{\text{t}}^T\text{X}\text{w}}{{\delta }^2}+\frac{-2{\mu }_0^T\text{w}}{{\Sigma }_0} \\ \frac{{\mu }_w^T}{{\Sigma }_w}=\frac{{\text{t}}^T\text{X}}{{\delta }^2}+\frac{{\mu }_0^T}{{\Sigma }_0} \\ {\mu }_w^T=(\frac{{\text{t}}^T\text{X}}{{\delta }^2}+\frac{{\mu }_0^T}{{\Sigma }_0}){\Sigma }_w \\ {\mu }_w={\Sigma }_w(\frac{1}{{\delta }^2}{\text{X}}^T\text{t}+{\Sigma }_0^{-1}{\mu }_0) \end{gathered}$$

由此$w$的均值方差计算完毕($p(\text{w}|\text{t},\text{X},{\delta }^2)$被计算出来了)，注意方差矩阵${\Sigma }_w$是对称阵，${\Sigma }_0$也是对称阵，那是因为它们里面的元素本来就是对角的而且全部相等。
比较一下${\mu }_w$与正则化最小二乘法
$$\begin{gathered} {\mu }_w=(\frac{1}{{\delta }^2}{\text{X}}^T\text{X}+{\Sigma }_0^{-1}{)}^{-1}(\frac{1}{{\delta }^2}{\text{X}}^T\text{t}+{\Sigma }_0^{-1}{\mu }_0) \\ w=({\text{X}}^T\text{X}+\lambda \text{I}{)}^{-1}{\text{X}}^T\text{t} \end{gathered}$$

如果${\mu }_0=[0,0,...,0{]}^T$，那么就变成了$${\mu }_w=(\frac{1}{{\delta }^2}{\text{X}}^T\text{X}+{\Sigma }_0^{-1}{)}^{-1}\frac{1}{{\delta }^2}{\text{X}}^T\text{t}$$

与正则化最小二乘法几乎没有差别。鉴于后验概率是高斯分布，$w$最有可能的唯一值是后验概率的均值${\mu }_w$，实际上这是后验分布，为什么这么说呢？因为它并没有用到分母，而是用很巧妙的方法绕过去了，但是既然能求出分布，那么它就是贝叶斯估计。

很多情况下，先验后验并不是共轭的(这很常见)，因此就不得不计算分母，又很难算，怎么办呢？就用到点估计，拉普拉斯近似，马尔科夫链-蒙特卡洛法。

点估计：样本均值估计整体均值，概论里的题，前提是知道分布是什么函数。

接下来讲log了！课本上讲的点估计就是用log推算一遍最大后验(吐血)，或者直接${\text{w}}^T\text{x}=0$。。。这跟点估计有什么关系啊？

拉普拉斯近似：很多时候，无法确定一个概率分布的具体密度函数，这时候则需要对这种无法精确知道分布函数的概率进行近似处理成已知的概率分布，从而方便计算或操作。拉普拉斯近似便是一种简单且广泛应用的近似方法。
该方法的目的是找到一组定义在连续变量变量上的高斯近似，当原始分布比较简单的时候效果会较好。然后通过泰勒展开式，在相应的地方展开。这里也不知道后验是什么函数，就硬生生展开，这时候一阶导是0(这是必须的，这是意义)删去，忽略3阶以上的，最后剩下一些式子，二阶导是海塞矩阵，是负的(负定)，然后这个式子与高斯取对数后极其相似！这就是拉普拉斯近似。我们用高斯密度近似后验，这个思想很容易扩展到多元密度，尤其是，拉普拉斯近似对真实后验$$p(\text{w}|\text{X},\text{t},{\delta }^2)\sim N(\mu ,\Sigma )$$

其中$\mu$设置为$w$，$\Sigma$是海塞矩阵逆的负。。。近似值是基于众数点函数属性得到的。

Markov Chain Monte Carlo (MCMC)二十世纪 top 10 之一的算法，假如我们有真正随机的均匀随机函数，那么我们怎么搞到高斯分布概率函数呢？
假如在 y 轴上产生（0,1）之间的均匀分布的随机数，水平向右投影到高斯累计分布函数上，然后垂直向下投影到 x 轴，得到的就是高斯分布。可见高斯分布的随机数实际就是均匀分布随机数在高斯分布的 CDF(累积分布，又叫分布函数，是概率密度函数的积分) 函数下的逆映射。当然，在实际操作中，更有效的计算方法有 Box–Muller_transform (an efficient polar form)，Ziggurat algorithm 等，这些方法 tricky and faster，没有深入了解，这里也不多说了。
MCMC 可解决高维空间里的积分和优化问题：

上面一个例子简单讲了利用高斯分布的 CDF 可以产生高斯随机数，但是有时候我们遇到一些分布的 CDF 计算不出来（无法用公式表示）(自然不是高斯函数了)，随机数如何产生？
遇到某些无法直接求积分的函数，如 e^{x2}，在计算机里面如何求积分？
如何对一个分布进行高效快速的模拟，以便于抽样？(这个是关键，我们要解决的问题)
如何在可行域很大(or large number of possible configurations)时有效找到最优解——RBM 优化目标函数中的问题。
如何在众多模型中快速找到更好的模型——MDL, BIC, AIC 模型选择问题。

实际上，Monte Carlo 抽样基于这样的思想：假设玩一局牌的赢的概率只取决于你抽到的牌，如果用穷举的方法则有 52! 种情况，计算复杂度太大。而现实中的做法是先玩几局试试，统计赢的概率，如果你不太确信这个概率，你可以尽可能多玩几局，当你玩的次数很大的时候，得到的概率就非常接近真实概率了。感觉就是点估计，只不过点估计的结果是函数，蒙特卡洛法得到的是结果(没有过程，不知道分布)。但是，当我们实际动手的时候，就会发现一个问题——如何从分布 p(x) 中抽取随机样本。之前我们说过，计算可以产生均匀分布的伪随机数。显然，第二小节产生高斯随机数的抽样方法只对少数特定的问题管用，对于一般情况呢？

什么是蒙特卡洛法？
就是随机投点计算圆周率的那个例子。

三门问题如何理解？（当然你可以用暴力蒙特卡洛算出）
比如说主持人和你做游戏，你有一个箱子，里面有1个球；主持人一个箱子，里面有2个球。他知道每个球的颜色，但你啥也不知道。但是3个球里面只有1个紫色的球，2个蓝色的球，谁手里面有紫色的球，谁就获得大奖。

主持人说：你要和我换箱子吗？
当然换，我箱子里只有1个球，中奖率$\frac{1}{3}$，他箱子里有2个球，中奖率$\frac{2}{3}$ ，换的中奖率是不换的2倍。
这是这个游戏的结论。现在情况变了：
主持人从他的箱子里扔了一个蓝色的球之后说：你要和我换箱子吗？
当然换，我箱子里只有1个球，中奖率$\frac{1}{3}$，他箱子里有2个球，中奖率$\frac{2}{3}$。扔了一个蓝色的，中奖率没变还是$\frac{2}{3}$，换的中奖率是不换的2倍。

蒙特卡洛算法实际上是大数定理的应用吧，同分布，有期望就行。蒙特卡罗法的核心是随机抽样(random sampling)。

下面是如何求积分

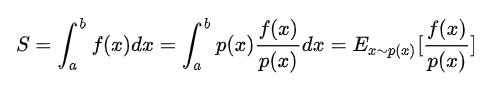
$p(x)$是一个分布，那么$\frac{f(x)}{p(x)}$就相当于$x$一样了。整体就会变成一个期望。然后估计这个期望值就用蒙特卡洛暴力法了，采样就是采用$p(x)$的概率分布采样，如果是均匀分布呢？实际上大一的积分估计介绍就是这么来的，蒙特卡洛的特例而已。这就足以证明其正确性了。

现在的问题转到了如何按照$p(x)$采样若干个样本上来。但是，按照$p(x)$采样绝非易事，因为有些时候我们根本不知道$p(x)$是什么，或者有时候是一个很复杂的表达式，计算机没法直接抽样。也就是说，$p(x)$也不是随随便便取的。
随机抽样方法1：拒绝-接受采样

随机抽样方法2：重采样技术reparameterization trick

我们需要大量采样，虽然我们有拒绝-接受采样和重采样技术，但是依旧面临采样困难的问题。巧了，马尔科夫链可以帮我们解决这个难题。

马尔科夫链你是知道是什么样的。如果我们得到了某个平稳分布所对应的马尔科夫链状态转移矩阵，我们就很容易采用出这个平稳分布的样本集。

Reject Sampling (拒绝取样)实际采用的是一种迂回( proposal distribution q(x) )的策略。既然 p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可抽样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，达到接近 p(x) 分布的目的

也就是说，我们用高斯近似了这个函数。

具体操作如下，设定一个方便抽样的函数 q(x)，以及一个常量 k，使得 p(x) 总在 kq(x) 的下方。（参考上图）

x 轴方向：从 q(x) 分布抽样得到 a。(如果是高斯，就用之前说过的 tricky and faster 的算法更快）
y 轴方向：从均匀分布（0, kq(a)) 中抽样得到 u。
如果刚好落到灰色区域： u > p(a), 拒绝， 否则接受这次抽样
重复以上过程(仍然是投针问题)
在高维的情况下，Rejection Sampling 会出现两个问题，第一是合适的 q 分布比较难以找到，第二是很难确定一个合理的 k 值。这两个问题会导致拒绝率很高，无用计算增加。
上面说了这么多采样方法，其实最终要突出的就是 MCMC 的过人之处。MCMC 的绝妙之处在于：通过稳态的 Markov Chain 进行转移计算，等效于从 P(x) 分布采样。

每日小常识
范数，是具有“长度”概念的函数。
欧式范数，实际上是$l_2$-范数
$$||x||=\sqrt{3^2+(-2{)}^2+1^2}=3.742$$
$l_p$-范数定义为
$$||x|{|}_p{=}^p\sqrt{\sum _i|x_i{|}^p}$$
例如$l_1$-范数定义为
$l_p$-范数定义为
$$||x|{|}_p=\sum _i|x_i|$$
$l_0$-范数表示非零项的个数。
实际上我们加的正则项是$l_2$-范数的。

一般迭代前后步骤的差值称为范数，用范数表示其大小。
常用的是二范数，差值越小表示越逼近实际值，可以认为达到要求的精度，收敛。范数本质是距离，存在的意义是为了实现比较

和向量的范数一样，矩阵也有范数，假设矩阵A的大小为m∗n，即m行n列。
$$||A|{|}_1=ma{x}_{j=1}^n\sum _{i=1}^m|a_{ij}|$$
先求每行的总和，最后找这几行中最大的那个总和。
2-范数，又名谱范数
$$||A|{|}_2=\sqrt{max({\lambda }_i)}$$
其中，${\lambda }_i$是$A^{T}A$的特征值。就是最大特征值的开平方。
F-范数，计算方式为矩阵元素的绝对值的平方和再开方。
无穷范数，又名行和范数，即矩阵行向量中绝对值之和的最大值。

范式球(norm ball)，为了便于可视化，我们考虑两维的情况，在(w1, w2)平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：

可以看到，两个轴是两个参数。两个参数被限制在了原点附近，这很好理解，上面的等高线圆表明在那个地方拟合度最好(仅仅拟合测试集，果不其然有过拟合)。就这么回事了。

再者说，什么是线性回归，指的是$w$，还是$x$？实际上指的是$x$，因为$w$永远是线性的。多项式回归模型是线性回归模型的一种，此时回归函数关于回归系数是线性的。注意这可是百科上说的。
如果将x2理解为一个特征，将x理解为另外一个特征,换句话说，本来我们的样本只有一个特征x，现在我们把他看成有两个特征的一个数据集。多了一个特征x2，那么从这个角度来看，这个式子依旧是一个线性回归的式子，但是从x的角度来看，他就是一个二次的方程。