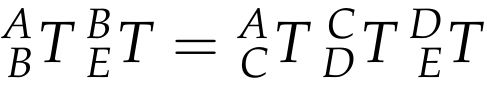Udacity机器人软件工程师课程笔记（十五）-运动学-正向运动学和反向运动学(其二)-DH参数等

正向运动学和反向运动学

目录

1. 2D中的旋转矩阵
2. sympy包
3. 旋转的合成
4. 旋转矩阵中的欧拉角
5. 平移
6. 齐次变换及其逆变换
7. 齐次变换的合成
8. Denavit-Hartenberg 参数
9. DH参数分配算法
10. 正向运动学
11. 反向运动学
12. 反向运动学举例

7.齐次变换的合成

齐次变换的合成与旋转的合成遵循着相同的逻辑。

假设从坐标系C到坐标系B的变换是已知的，从坐标系B到坐标系a的变换也是已知的。
${}^C\mathbf{r}P/Co$关于坐标系_$A$首先将它转化为坐标系$B$，

(6-1)

然后通过变换到A坐标系，

(6-2)

(6-1)(6-2)式可以组合为:

为了完整起见，把A和C之间的变换展开成已知的分量，
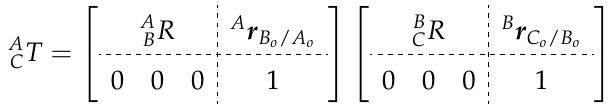(6-3)
（6-4）

式(6-4)中的左上3x3子矩阵看起来应该很熟悉;它是a和C之间旋转的组合。

${}_B^A{R}^{B}rCo/Bo$是向量从$B_o$到$Co$在_A坐标系中的表示。另一项，${}^A{\mathbf{r}}_{Bo/Ao}$是向量从$A_o$到$B_o$在_A坐标系中的表示。

为了帮助巩固变换、逆变换和变换组合的概念，再考虑一个例子。这里是坐标系A到E。
假设我们想要创建坐标系A和E之间的变换;显然，有两条路。一条路径有变换，

（6-5）

第二个是：

（6-6)

两者的结果相同

（6-7)

下面程序是证明（7）式，经过两种途径， 实现坐标系从A到E的变换

从A系到B系到E系:
坐标系A:位于[0,0,0]
坐标系B:将坐标系A旋转大约a_y -90度。翻译A by [- 2,2,4]
坐标系E:将坐标系B旋转约b_x 90度。将B平移[0,2,0]

从A系到C系到D系到E系:
坐标系C:平移A到[4,4,0]
坐标系D:围绕c_x旋转坐标系C 90度。翻译C by [- 3,3, 2]
坐标系E:围绕d_Z旋转坐标系D 90度。将D平移[- 3,2,3]

from sympy import symbols, cos, sin, pi, sqrt, simplify
from sympy.matrices import Matrix

# 为联合变量创建符号
# 数字1到4按指定的顺序对应于每个旋转。
q1, q2, q3, q4 = symbols('q1:5')


# 定义关于给定特定角度的x、y和z的旋转矩阵的函数。

def rot_x(q):
    R_x = Matrix([[1, 0, 0],
                  [0, cos(q), -sin(q)],
                  [0, sin(q), cos(q)]])

    return R_x


def rot_y(q):
    R_y = Matrix([[cos(q), 0, sin(q)],
                  [0, 1, 0],
                  [-sin(q), 0, cos(q)]])

    return R_y


def rot_z(q):
    R_z = Matrix([[cos(q), -sin(q), 0],
                  [sin(q), cos(q), 0],
                  [0, 0, 1]])

    return R_z


# 定义坐标系之间的旋转

# 坐标系A的初始旋转矩阵
Ra = Matrix([[1, 0, 0],
             [0, 1, 0],
             [0, 0, 1]])

# 在A->B->E坐标系上进行旋转
Rb_a = rot_y(q1)
Re_b = rot_x(q2)

# 在A->C->D->E坐标系上进行旋转
Rc_a = Ra
Rd_c = rot_x(q3)
Re_d = rot_z(q4)

# 定义坐标系之间的转换

tb_a = Matrix([[-2], [2], [4]])
te_b = Matrix([[0], [2], [0]])
tc_a = Matrix([[4], [4], [0]])
td_c = Matrix([[-3], [3], [2]])
te_d = Matrix([[-3], [2], [3]])

# 定义齐次变换矩阵
Ta = Ra.row_join(Matrix([[0], [0], [0]]))
Ta = Ta.col_join(Matrix([[0, 0, 0, 1]]))

Tb_a = Rb_a.row_join(tb_a)
Tb_a = Tb_a.col_join(Matrix([[0, 0, 0, 1]]))

Te_b = Re_b.row_join(te_b)
Te_b = Te_b.col_join(Matrix([[0, 0, 0, 1]]))

Tc_a = Rc_a.row_join(tc_a)
Tc_a = Tc_a.col_join(Matrix([[0, 0, 0, 1]]))

Td_c = Rd_c.row_join(td_c)
Td_c = Td_c.col_join(Matrix([[0, 0, 0, 1]]))

Te_d = Re_d.row_join(te_d)
Te_d = Te_d.col_join(Matrix([[0, 0, 0, 1]]))

# 化简公式
Te_a_1 = simplify(Ta * Tb_a * Te_b)

Te_a_2 = simplify(Ta * Tc_a * Td_c * Te_d)

# 计算E的方向和位置
E_1 = Te_a_1.evalf(subs={q1: -pi / 2, q2: pi / 2}, chop=True)

E_2 = Te_a_2.evalf(subs={q3: pi / 2, q4: pi / 2}, chop=True)

print('E_1 :',E_1)
print('E_2 :',E_2)

有关更多sympy表达式化简的在这里。

输出如下：

E_1 : Matrix([[0, -1.00000000000000, 0, -2.00000000000000], [0, 0, -1.00000000000000, 4.00000000000000], [1.00000000000000, 0, 0, 4.00000000000000], [0, 0, 0, 1.00000000000000]])
E_2 : Matrix([[0, -1.00000000000000, 0, -2.00000000000000], [0, 0, -1.00000000000000, 4.00000000000000], [1.00000000000000, 0, 0, 4.00000000000000], [0, 0, 0, 1.00000000000000]])

由此看出，经过两个变换，两者得出来的结果是相同的。

8.Denavit-Hartenberg 参数

在前面的课程中，介绍了旋转、平移和齐次变换的概念。所有这些概念对于理解机械手正运动学问题都是必不可少的，即给定关节变量，计算末端执行器的位置。求解过程包括在机械手的每个连杆上附加一个参照系，并写出从固定基座连杆到连杆1、从连杆1到连杆2的齐次变换，一直到末端执行器。

（7-1）

通常，每个变换需要6个独立的参数来描述相对于坐标系$i-1$的坐标系$i$, 3个参数表示位置，3个参数表示方向。

1955年，雅克·德纳维特(Jacques Denavit)和理查德·哈滕伯格(Richard Hartenberg)提出了一种将参照系附加到机械手连杆上的系统方法，简化了齐次变换。他们的方法只需要四个参数来描述相邻参考系的位置和方向。在机器人技术的早期，更紧凑的正运动学方程提供了巨大的好处，因为计算通常是人工或在处理能力有限的计算机上进行的。因此，用于描述机械手运动学的Denavit-Hartenberg (DH)方法现在是普遍存在的。

自最初的描述以来，DH方法已经做了一些修改，主要是关于每个参考系原点的编号和位置，所以在比较来自不同来源的工作时，必须小心确定使用的是哪种约定。以下是五个最常见的来源，

• Waldron, KJ. A study of overconstrained linkage geometry by solution of closure equations, Part I: A method of study (1973). Mech. Mach. Theory 8(1):95-104.

• Paul, R. (1982). Robot Manipulators: Mathematics, Programming and Control (MIT Press, Cambridge, MA)

• Craig, JJ. (2005). Introduction to Robotics: Mechanics and Control, 3rd Ed (Pearson Education, Inc., NJ)(机器人学概论:机械与控制，第三版)

• Khalil, W and Dombre, E. (2002). Modeling, Identification and Control of Robots (Taylor Francis, NY)

• M. Spong and M. Vidyasagar, Robot Modeling and Control, Wiley, 2005

这里使用John J Craig书中描述的约定。

这些惯例上的差异使得比较结果更加困难。重要的是始终检查齐次变换序列是如何执行的，以关联相邻的连接。下面描述的约定与Craig(2005)一致。涉及的参数 α，a，d和θ。
参数名称和定义总结如下:

• ${\alpha }_{i-1}$(扭转角) = 沿${\hat{X}}_{i-1}$以右手法则观测的 ${\hat{Z}}_{i-1}$和${\hat{Z}}_i$之间的夹角。
• $a_{i-1}$ (连杆长度) = 沿${\hat{X}}_{i-1}$测量的从${\hat{Z}}_{i-1}$到${\hat{Z}}_i$的距离，且${\hat{X}}_{i-1}$是垂直于 ${\hat{Z}}_{i-1}$和${\hat{Z}}_i$的。
• $d_i$(连接偏移) = 沿${\hat{Z}}_i$观测的${\hat{X}}_{i-1}$和${\hat{X}}_i$之间的有符号距离。注意，这个量在棱柱连接（移动副）的情况下是一个变量。
• ${\theta }_i$ (关节角度) = 沿着${\hat{Z}}_i$以右手法则观测的${\hat{X}}_{i-1}$和${\hat{X}}_i$之间的夹角。注意，对于转动连接（转动副），这个量是一个变量。

关于连接方式，参考这里。

对于一个n自由度的机械手，将有n个关节{1,2，…，n}，由于每个关节连接两个连杆，所以有n+1个连杆{0,1，…，n}。按照惯例，固定的基本链接为链接0，索引$i$朝着末端执行器顺序增加。注意，如上面的图所示，并不要求坐标系的原点在连接点上，只是要求它与连接点一起严格移动。坐标系的z轴，在转动连接的情况下，与关节的旋转轴对齐。因此，相对于连接$i-1$,连接$i$绕${\hat{Z}}_i$旋转。对于棱形联接，z轴与其运动方向一致。

一个与两个向量相互垂直的单位向量定义为，

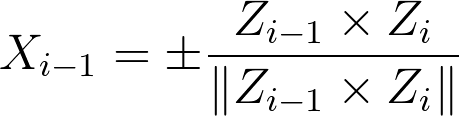
(7-2)
即，向量的叉乘除以向量叉乘的模。只有在倾斜轴的情况下，${\hat{X}}_{i-1}$是唯一的。对于相交轴，符号的选择是任意的。通常的做法是选择${\hat{X}}_{i-1}$的方向，使连接$i$的正向旋转到合适的位置。

对于平行的轴，有无限多种可能。在这种情况下，应该寻找机会将参考系的原点放在它可以使其他一些参数等于零的位置。

最后，选择y轴来完成一个右手坐标系。

从坐标系$i-1$到坐标系$i$的齐次变换是由四个基本变换、两个旋转和两个平移组成的矩阵，如下所示

(7-3)

(7-4)

方程(7-1)和(7-3)的理解非常重要。当

学习为一个新的机械手编写DH参数时，经常会纠结于在哪里放置参考帧，如何定位它们，以及跟踪索引。我们应该经常问自己的一个问题是:“变换是否移动了连接$i-1$中的参考系，使其与连接$i$中的参考系完全一致?”如果答案是肯定的，这是一个好的迹象。

同样重要的是，在式(7-3)中，只有一个参数是可变的 (${\theta }_i$或$d_i$) ，连杆长度和扭转角是常数。因此，对于从基础连接到末端执行器${}_n^{0}T$的整个变换，只有n个变量。

9.DH参数分配算法

上一课试图解释DH参数背后的理论和动机。现在的重点是如何在算法上为操纵器的链接分配参考坐标系。请记住，坐标系$i-1$牢固地连接到坐标系$i$。为了方便起见，接着用上面的图

具有n个自由度的运动链（即关节）的参数分配过程总结为：

1. 标记{1，2，…，n }中的所有关节。

2. 将{0，1，…，n}中的所有链接标记为固定的基本链接为0。

3. 在所有关节上画线，定义关节轴。

4. 分配每个框架的Z轴指向其关节轴。

5. 在${\hat{Z}}_{i-1}$和 ${\hat{Z}}_i$之间识别每个坐标系的共同法线 。

6. “中间链接”（即，不是基础链接或末端执行器。）的端点与两个关节轴$i$和$i+1$相关联。对于从1到n-1的$i$，将${\hat{X}}_i$赋值为：

   • 对于倾斜轴，沿法线之间 ${\hat{Z}}_i$ 和${\hat{Z}}_{i+1}$，并从$i$指向$i+1$。

   • 对于相交轴，垂直于包含 ${\hat{Z}}_i$ 和 ${\hat{Z}}_{i+1}$。

   • 对于平行轴或重合轴，分配是任意的；寻找使其他DH参数等于零的方法。

7. 对于基本链接，当第一个关节变量（${\theta }_1$或者$d_1$）为0时，总是选择坐标系$0$与坐标系$1$重合。这将保证 ${\alpha }_0$ = 0。注意，如果关节1是转动的，则 连接偏移$d_1$ =0。如果关节1是棱柱形的，则 转动角度${\theta }_1=0$。

8. 对于末端执行器坐标系，如果关节n是转动关节。 当${\theta }_n$ = 0和坐标系n的原点即 $d_n$ = 0，选择 $X_n$朝向 $X_{n-1}$。

进行坐标系分配后，DH参数通常以表格形式显示（如下）。表中的每一行都对应于从坐标系$i$到坐标系$i+1$的转换。

这是一些DH参数简化，以便在选择框架任务时寻找。

• 涉及到坐标轴${\hat{Z}}_{i-1}$到坐标轴${\hat{Z}}_i$的特殊情况：
  • 共线：$\alpha =0$ and a = 0
  • 平行：$\alpha =0$ and a $\ne$ 0
  • 相交：$\alpha \ne 0$ and a = 0
  • 如果公共法线在坐标系i的原点与${\hat{Z}}_i$相交，那么$d_i$ = 0

不同的作者提出了多种分配DH参数的约定。即使两个分析人员使用相同的约定，也无法保证将导致相同的坐标系分配给链接。但是，如果选择相同的基本框架和相同的点作为框架n的原点，则无论使用哪种约定，从0到n的整体转换都将是相同的。

10.正向运动学

正向运动学问题归结为齐次变换的合成。我们从基础链接开始，然后逐个链接移动到末端执行器。并且使用DH参数来构建每个单独的变换。

相邻连接的总变换实际上由四个单独的转换组成，2个旋转和2个平移。以SCARA为例，
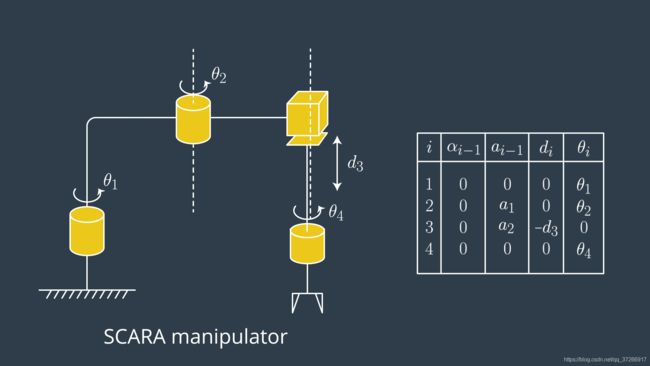
按照介绍的DH参数的8步分布过程，我们可以得到右面这个表格。注意每一行只有一个变量（${\theta }_1$或者$d_1$）。

程序如下：

首先从SymPy导入几个组件。

from sympy import symbols, cos, sin, pi, simplify
from sympy.matrices import Matrix

接下来，我们定义将在变换方程中使用的符号。在这里，我用q表示广义坐标；d，a和alpha是其他DH参数。

### Create symbols for joint variables
q1, q2, q3, q4 = symbols('q1:5')
d1, d2, d3, d4 = symbols('d1:5')
a0, a1, a2, a3 = symbols('a0:4')
alpha0, alpha1, alpha2, alpha3 = symbols('alpha0:4')

对于非零常数DH参数，使用数值进行表达。

a12 = 0.4500 # meters
a23 = 0.3000 # meters

在这里，建立了一个字典，将数字值绑定到那些常量的DH参数上。

# DH Parameters
s = {alpha0: 0,  a0:   0, d1: 0, 
     alpha1: 0,  a1: a12, d2: 0,  
     alpha2: 0,  a2: a23, q3: 0,
     alpha3: 0,  a3:   0, d4: 0}

然后，定义相邻链接之间的齐次变换，并使用subs方法将已知的常数值替换为表达式。

# 齐次变换
T0_1 = Matrix([[             cos(q1),            -sin(q1),            0,              a0],
               [ sin(q1)*cos(alpha0), cos(q1)*cos(alpha0), -sin(alpha0), -sin(alpha0)*d1],
               [ sin(q1)*sin(alpha0), cos(q1)*sin(alpha0),  cos(alpha0),  cos(alpha0)*d1],
               [                   0,                   0,            0,               1]])
T0_1 = T0_1.subs(s)

T1_2 = Matrix([[             cos(q2),            -sin(q2),            0,              a1],
               [ sin(q2)*cos(alpha1), cos(q2)*cos(alpha1), -sin(alpha1), -sin(alpha1)*d2],
               [ sin(q2)*sin(alpha1), cos(q2)*sin(alpha1),  cos(alpha1),  cos(alpha1)*d2],
               [                   0,                   0,            0,               1]])
T1_2 = T1_2.subs(s)

T2_3 = Matrix([[             cos(q3),            -sin(q3),            0,              a2],
               [ sin(q3)*cos(alpha2), cos(q3)*cos(alpha2), -sin(alpha2), -sin(alpha2)*d3],
               [ sin(q3)*sin(alpha2), cos(q3)*sin(alpha2),  cos(alpha2),  cos(alpha2)*d3],
               [                   0,                   0,            0,               1]])
T2_3 = T2_3.subs(s)

T3_4 = Matrix([[             cos(q4),            -sin(q4),            0,              a3],
               [ sin(q4)*cos(alpha3), cos(q4)*cos(alpha3), -sin(alpha3), -sin(alpha3)*d4],
               [ sin(q4)*sin(alpha3), cos(q4)*sin(alpha3),  cos(alpha3),  cos(alpha3)*d4],
               [                   0,                   0,            0,               1]])
T3_4 = T3_4.subs(s)

最后，通过组合各个链接变换来创建基础框架和末端执行器之间的整体变换。

# Transform from base link to end effector
T0_4 = simplify(T0_1 * T1_2 * T2_3 * T3_4)

print命令显示整体变换。

print(T0_4)

对符号表达式进行数值计算的方法有很多，一种简单的方法是使用evalf方法并传入字典。

print(T0_4.evalf(subs={q1: 0, q2: 0, d3: 0, q4: 0}))

输出如下：

Matrix([[cos(q1 + q2 + q4), -sin(q1 + q2 + q4), 0, 0.45*cos(q1) + 0.3*cos(q1 + q2)], [sin(q1 + q2 + q4), cos(q1 + q2 + q4), 0, 0.45*sin(q1) + 0.3*sin(q1 + q2)], [0, 0, 1, d3], [0, 0, 0, 1]])
Matrix([[1.00000000000000, 0, 0, 0.750000000000000], [0, 1.00000000000000, 0, 0], [0, 0, 1.00000000000000, 0], [0, 0, 0, 1.00000000000000]])

11.反向运动学

反向运动学（IK）本质上与正向运动学相反。在这种情况下，末端执行器的姿势（即位置和方向）是已知的，目标是计算操纵器的关节角度。但是，IK问题更具挑战性。正如我们在DH参数课程中所看到的，相邻链接之间的均匀变换为：

因此，对于具有n个关节的操纵器，基础执行器和末端执行器之间的整体转换涉及方程式（1）的n倍。显然，这会导致复杂的，高度非线性的方程，这些方程通常具有零个或多个解。此外，这些数学解实际上可能违反了现实世界的联合限制，因此在数学上可能的解中进行选择时需要格外小心。让我们暂停片刻，思考一下这些不同解决方案的物理含义。

考虑“拟人”（RRR）机械手的情况。名称来自以下事实：关节1类似于人的髋关节（想象在腰部绕垂直轴扭曲），关节2是“肩膀”，关节3是“肘”。如果我们只关心末端执行器的位置，则有四种可能的方法可以到达操纵器工作空间中的3D点。注意每个旋转关节上的阴影。第一行对应于“弯头”解决方案。第1列对应髋关节=θ的解，第2列对应髋关节=θ+π的解。

有两种不同的解决方法可以解决IK问题。第一种是纯数值方法。本质上，此方法是猜测式的，并且会反复进行，直到错误足够小或花了很长时间使放弃为止。Newton-Raphson算法是一种常见选择，因为它在概念上很简单，并且如果初始猜测“足够接近”该解，则收敛速度为二次方。但是，不能保证算法会收敛或快速收敛到足以满足应用程序要求的程度，并且只能返回一种解决方案。为了生成各种可能姿势的解决方案，必须使用不同的初始条件。数值方法的优点在于，相同的算法适用于所有串行操纵器。

另一种且更优选的方法是已知的“分析”或“封闭形式”。封闭形式的解决方案是不需要迭代即可求解的特定代数方程式，它具有两个主要优点：通常，它们比数值方法求解速度快得多，并且更容易为相应的可能解决方案制定规则。一。但是，只有某些类型的操纵器可以闭合形式求解。显而易见的问题是，那么哪种类型的操纵器具有封闭形式的解决方案？研究表明，如果满足以下两个条件之一，则串行机械手可以闭合形式求解。

1. 三个相邻的关节轴在单个点处相交，或者
2. 三个相邻的关节轴是平行的（从技术上讲，这是1的特例，因为平行线在无限远处相交）

幸运的是，目前工业上使用的六种DoF串行操纵器中的大多数将满足上述条件之一。

机械手中的最后三个关节通常是满足条件1的旋转关节。这种设计称为球形腕，而相交的公共点称为腕中心。这种设计的优点在于，它在运动学上解耦了末端执行器的位置和方向。从数学上讲，这意味着可以解决十二个问题非线性方程（同时在整个齐次变换矩阵的前三行中为每个项建立一个方程），现在可以独立解决两个简单的问题：首先是腕部中心的笛卡尔坐标，然后是调整末端执行器的方向。从物理上讲，具有球形腕部的六自由度串行机械手将使用前三个关节来控制腕部中心的位置，而最后三个关节将根据需要对末端执行器进行定向。

现在，我们将正式确定带球形腕的串行机械手的解决方法。考虑此处所示的六自由度机械手，其中关节4、5和6包括球形手腕。腕部中心（WC）和末端执行器（EE）相对于底架“ 0”的位置由下式给出：

${}^0{\mathbf{r}}_{WC/0}$和${}^0{\mathbf{r}}_{EE/0}$。

EE相对于WC的位置由下式给出：${}^0{\mathbf{r}}_{WC/EE}$ 。

注意，所有三个向量均以基础坐标系表示，如前导上标“ 0”所示。
步骤1： 完成机械手的DH参数表。提示：将第4、5和6帧的原点与WC重合。

步骤2： 查找WC相对于基础框架的位置。回想一下，基础执行器和末端执行器之间的整体同类转换具有以下形式，

例如，如果选择z4平行于z6，并且从WC指向EE，那么这个位移就是沿着z6的简单平移。这个位移的大小，记为d，取决于机械手的尺寸，在URDF文件中定义。此外，由于r13、r23和r33定义了EE相对于基坐标系的z轴，WC的笛卡尔坐标为，

步骤3: 求出关节变量q1 q2 q3，使得WC的坐标为式(3)，这一步比较难。解决这一问题的一种方法是反复将连杆投影到平面上，并用三角函数求解关节角。不幸的是，没有一种通用的配方适用于所有的操作器，所以必须进行试验。

步骤4: 已知前三个关节变量后，计算${}_0^{3}R$通过应用齐次变换得到WC。

步骤5: 找到一组与旋转矩阵对应的欧拉角，

步骤6 **：从一组可能的解决方案中选择正确的解决方案

12.反向运动学举例

点$z_c$可以认为是球形手腕的手腕中心。假设$z_c$的笛卡尔坐标已经计算出来。要找到${\theta }_1$，我们需要将$z_c$投影到地平面上。这是一个很简单的任务，只需要将z坐标设置为0。

从而，

${\theta }_1=\mathbf{a}\mathbf{t}\mathbf{a}\mathbf{n}2({\mathbf{y}}_{\mathbf{c}},{\mathbf{x}}_{\mathbf{c}})$

${\mathbf{r}}^2={\mathbf{x}}_{\mathbf{c}}^2+{\mathbf{y}}_{\mathbf{c}}^2$

$\mathbf{s}={\mathbf{z}}_{\mathbf{c}}-{\mathbf{d}}_1$

最后一个关节变量d3表示移动关节的长度。从图中可以看出，d3是一个直角三角形的斜边，边为r和s。解d3,

${\mathbf{d}}_3=\sqrt{{\mathbf{r}}^2+{\mathbf{s}}^2}=\sqrt{{\mathbf{x}}_{\mathbf{c}}^2+{\mathbf{y}}_{\mathbf{c}}^2+({\mathbf{z}}_{\mathbf{c}}-{\mathbf{d}}_1{)}^2}$

前三个联合变量现在以封闭的形式显式地描述。