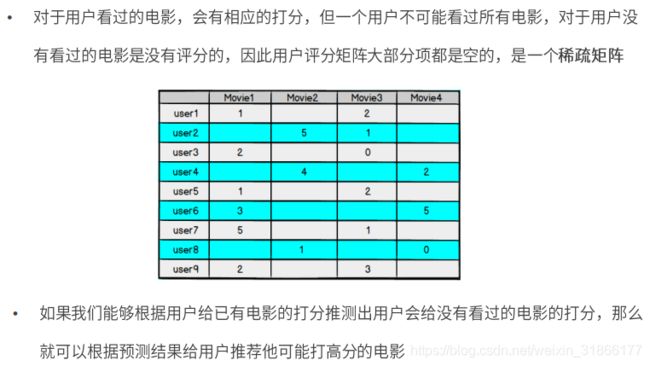
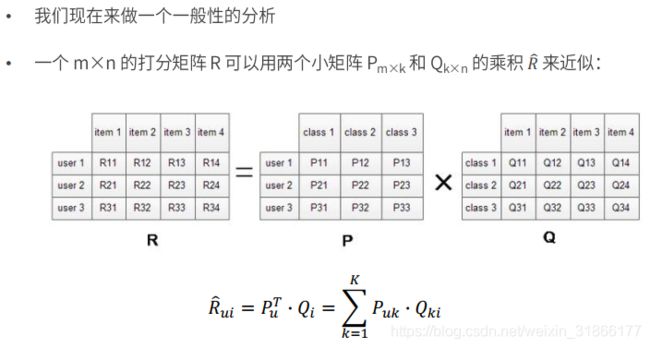
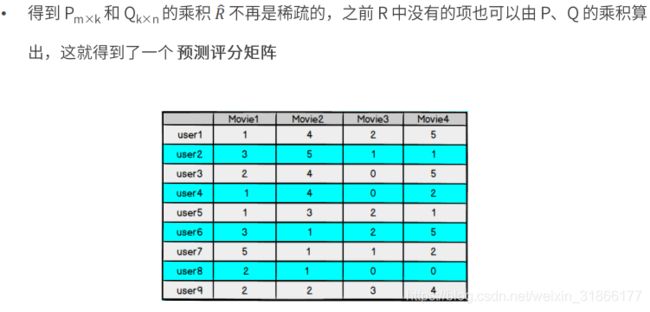
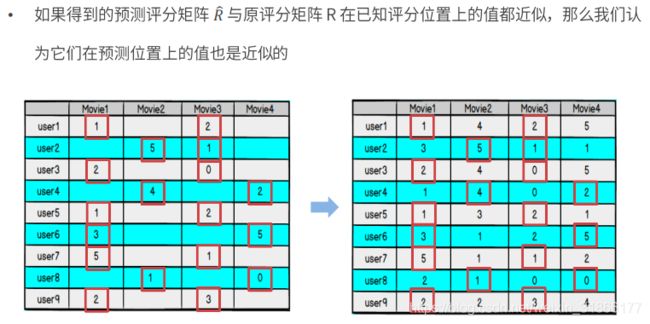
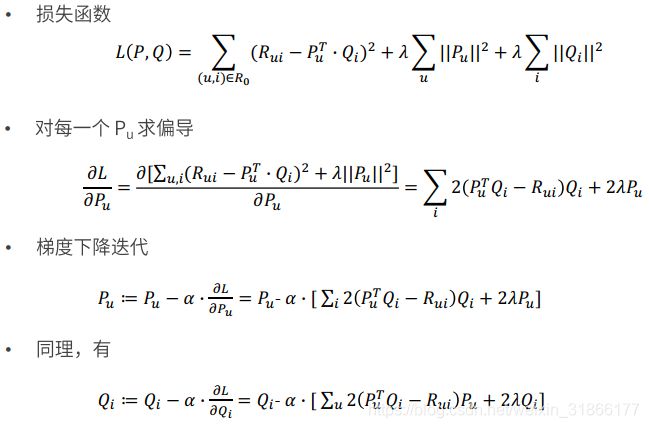【推荐系统】LFM梯度下降算法
目录
基于模型的cf思想
隐语义模型(LFM)
LFM降维方法——矩阵因子分解
矩阵因子分解
LFM的进一步理解
矩阵因子分解
模型求解——损失函数
模型的求解算法——ALS
ALS算法
梯度下降算法
LFM梯度下降算法代码实现
基于模型的cf思想
隐语义模型(LFM)
LFM降维方法——矩阵因子分解
矩阵因子分解
LFM的进一步理解
矩阵因子分解
模型求解——损失函数
模型的求解算法——ALS
ALS算法
梯度下降算法
LFM梯度下降算法代码实现
import numpy as np
import pandas as pd
# 评分矩阵R
R = np.array([[4,0,2,0,1],
[0,2,3,0,0],
[1,0,2,4,0],
[5,0,0,3,1],
[0,0,1,5,1],
[0,3,2,4,1],])
len(R[0])
"""
@输入参数:
R:M*N 的评分矩阵
K:隐特征向量维度(代表模型复杂度)
max_iter: 最大迭代次数
alpha:步长
lamda:正则化系数
@输出:
分解之后的 P,Q
P:初始化用户特征矩阵M*K
Q:初始化物品特征矩阵N*K
"""
# 给定超参数
K = 5
max_iter = 5000
alpha = 0.0002
lamda = 0.004
# 核心算法
def LFM_grad_desc( R, K=2, max_iter=1000, alpha=0.0001, lamda=0.002 ):
# 基本维度参数定义
M = len(R)
N = len(R[0])
# P,Q初始值,随机生成
P = np.random.rand(M, K)
Q = np.random.rand(N, K)
Q = Q.T
# 开始迭代
for step in range(max_iter):
# 对所有的用户u、物品i做遍历,对应的特征向量Pu、Qi梯度下降
for u in range(M):
for i in range(N):
# 对于每一个大于0的评分,求出预测评分误差
if R[u][i] > 0:
eui = np.dot( P[u,:], Q[:,i] ) - R[u][i]
# 代入公式,按照梯度下降算法更新当前的Pu、Qi
for k in range(K):
P[u][k] = P[u][k] - alpha * ( 2 * eui * Q[k][i] + 2 * lamda * P[u][k] )
Q[k][i] = Q[k][i] - alpha * ( 2 * eui * P[u][k] + 2 * lamda * Q[k][i] )
# u、i遍历完成,所有特征向量更新完成,可以得到P、Q,可以计算预测评分矩阵
predR = np.dot( P, Q )
# 计算当前损失函数
cost = 0
for u in range(M):
for i in range(N):
if R[u][i] > 0:
cost += ( np.dot( P[u,:], Q[:,i] ) - R[u][i] ) ** 2
# 加上正则化项
for k in range(K):
cost += lamda * ( P[u][k] ** 2 + Q[k][i] ** 2 )
if cost < 0.0001:
break
return P, Q.T, cost
# 测试
P, Q, cost = LFM_grad_desc(R, K, max_iter, alpha, lamda)
print(P)
print(Q)
print(cost)
predR = P.dot(Q.T)
print(R)
predR