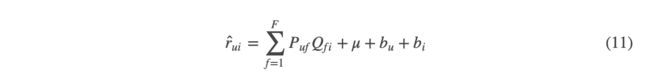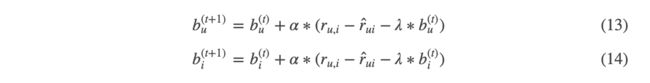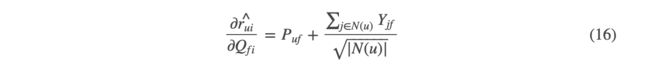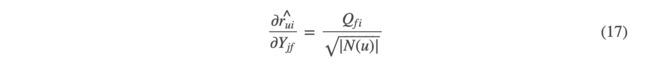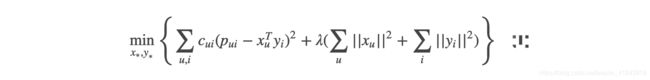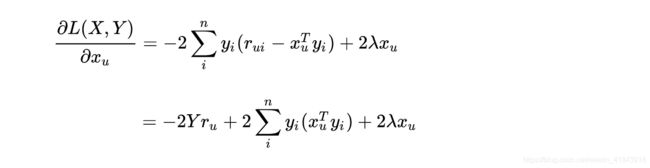推荐系统之---LFM的各种版本
1.说明
在推荐系统中有两种协同过滤的方式。
- 一种是基于邻域的方式,这种方式又包含了基于用户的和基于物品的,这种方式实现简单,而且效果也是非常的不错,唯一的缺点是对待稀疏矩阵的时候表现乏力。因此诞生了下面的方式。
- 方式二是基于模型的方式,也就是矩阵分解的方式,这种方式将推荐问题转化为了机器学习问题。
下面通过一个图来说明,不再详细介绍原理,而是主要分析各种LFM实现的变种
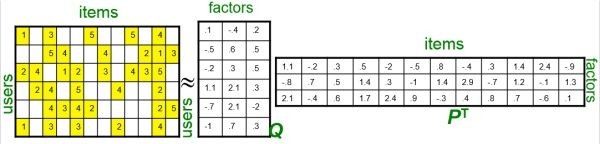
- 上图的大矩阵可以就是user-item的评分矩阵,而后面的就是分解出来的两个小矩阵分别为Q矩阵和P矩阵。
- 其中 Q矩阵是用户的因子矩阵;而P矩阵就是物品的因子矩阵。
- 两个小矩阵通过K个隐因子相连,最后通过最优化的方式计算出小矩阵的元素。
- 其实从物理意义上讲,可以理解为这是讲稀疏的大矩阵中的信息,浓缩到了两个小矩阵中。
2.LFM模型
原理在上面已经简单介绍。
假设我们已有有了一个评分矩阵 R m , n , m R_{m,n},m Rm,n,m个用户对 n n n个物品的评分全在这个矩阵里,当然这是一个高度稀疏的矩阵,我们用 r u , i r_{u,i} ru,i表示用户 u u u对物品 i i i的评分。LFM认为 R m , n = P m , F ⋅ Q F , n R_{m,n}=P_{m,F}·Q_{F,n} Rm,n=Pm,F⋅QF,n即R是两个矩阵的乘积(所以LFM又被称为矩阵分解法,MF,matrix factorizationmodel),F是隐因子的个数;P的每一行代表一个用户对各个隐因子的喜好程度;Q的每一列代表一个物品在各个隐因子上的概率分布。
- 下面的公式即为LFM的模型: r ^ \hat r r^表示的是预测评分
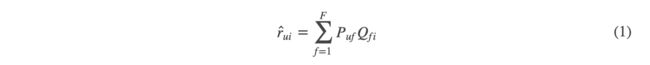
- 下面即为LFM的目标函数: r u , i r_{u,i} ru,i表示用户u对物品i的真实评分
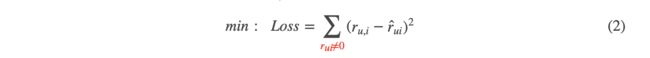
- 为了防止overfitting,添加正则项控制过拟合。

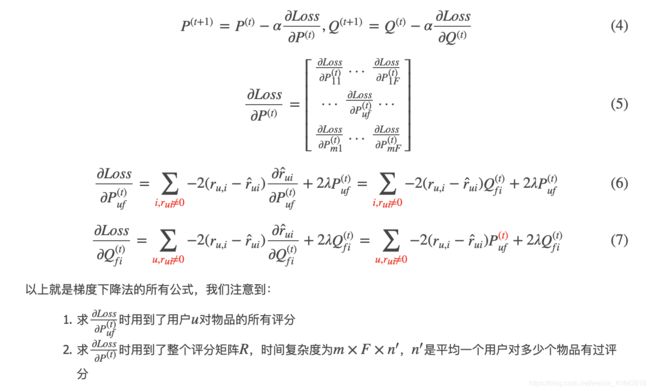
- 求解最优解的方式有两种分别为梯度下降法和交替最小二乘法,下面采用梯度下降法的求解上面的无约束最优化问题。
- 随机梯度下降法(SGD)没有严密的理论证明,但是在实践中他通常比传统的梯度下降法需要更少的迭代次数就可以收敛,他有两个特点:
- SGD单轮迭代的时间复杂度也是 m ∗ F ∗ n ′ m*F*n' m∗F∗n′,但由于它是单个参数地更新,且更新单个参数时只利用到一个样本(一个评分),更新后的参数立即可用于更新剩下的参数,所以SGD比传统的梯度下降需要更少的迭代次数。
- 在训练模型的时候我们只要求模型尽量拟合 r u , i r_{u,i} ru,i不为0的位置即可,对于为0的情况我们也不希望 r ^ u , i \hat r_{u,i} r^u,i为0,因为 r ^ u , i \hat r_{u,i} r^u,i为0只表示用户没有评价过,并不代表用户对物品的喜好为0。而恰恰 r ^ u , i \hat r_{u,i} r^u,i能反映用户u对物品i的喜好程度,然后根据喜好程度排序,就可以完成推荐。
- 代码实现。
# _*_coding:utf-8 _*_
__author__ = "ricky"
import random
import math
class LFM(object):
def __init__(self, rating_data, F, alpha=0.1, lmbd=0.1, max_iter=500):
"""
:param rating_data: rating_data是[(user,[(item,rate)]]类型
:param F: 隐因子个数
:param alpha: 学习率
:param lmbd: 正则化
:param max_iter:最大迭代次数
"""
self.F = F
self.P = dict() # R=PQ^T,代码中的Q相当于博客中Q的转置
self.Q = dict()
self.alpha = alpha
self.lmbd = lmbd
self.max_iter = max_iter
self.rating_data = rating_data
'''随机初始化矩阵P和Q'''
for user, rates in self.rating_data:
self.P[user] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
for item, _ in rates:
if item not in self.Q:
self.Q[item] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
def train(self):
"""
随机梯度下降法训练参数P和Q
:return:
"""
for step in range(self.max_iter):
for user, rates in self.rating_data:
for item, rui in rates:
hat_rui = self.predict(user, item)
err_ui = rui - hat_rui
for f in range(self.F):
self.P[user][f] += self.alpha * (err_ui * self.Q[item][f] - self.lmbd * self.P[user][f])
self.Q[item][f] += self.alpha * (err_ui * self.P[user][f] - self.lmbd * self.Q[item][f])
self.alpha *= 0.9 # 每次迭代步长要逐步缩小
def predict(self, user, item):
"""
:param user:
:param item:
:return:
预测用户user对物品item的评分
"""
return sum(self.P[user][f] * self.Q[item][f] for f in range(self.F))
if __name__ == '__main__':
'''用户有A B C,物品有a b c d'''
rating_data = list()
rate_A = [('a', 1.0), ('b', 1.0)]
rating_data.append(('A', rate_A))
rate_B = [('b', 1.0), ('c', 1.0)]
rating_data.append(('B', rate_B))
rate_C = [('c', 1.0), ('d', 1.0)]
rating_data.append(('C', rate_C))
lfm = LFM(rating_data, 2)
lfm.train()
for item in ['a', 'b', 'c', 'd']:
print(item, lfm.predict('A', item)) # 计算用户A对各个物品的喜好程度
3.带偏置的LFM(SVD)
- 偏置:把独立于用户或者独立于物品的的因素称为偏置部分。
- 个性化:将用户和物品的交互,也就是表示用户对物品的喜好的部分称为个性化部分。
- 在Netflix Prize推荐比赛中,Yehuda Koren仅使用偏置部分可以将评分误差降低32%,而加入个性化部分能降低42%,也就是说只有10%是个性化部分的作用,这也说明了偏置部分的重要性,剩下的58%的误差Yehuda Koren将其称之为模型不可解释部分,包括数据的噪音等因素。
- 将上面的公式(1)中加入偏置:
- 下面对偏置进行解释:
- μ \mu μ代表训练集中所有评分记录的全局平均数,表示了训练数据的总体评分情况,对于固定的数据集,他是一个常数。
- b u b_u bu代表用户偏置,独立于物品特征的因素,表示某一特定用户的打分习惯。比如,对于性格较为严苛的用户,打分会比较低;对于较为温和的用户,打分会偏高。
- b i b_i bi代表物品偏置,独立于用户兴趣的因素,表示一特定物品得到打分的情况。比如,好的影片的总体评分偏高,而烂片获得的评分普遍偏低,物品偏置捕获的就是这样的特征。
- 其中要说明的一点, μ \mu μ是一个统计值; b u b_u bu和 b i b_i bi需要通过模型训练得到,那么如此对比上面的公式(3)目标函数变为:
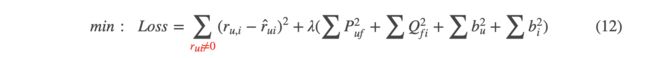
- 由梯度下降法得到 b u b_u bu和 b i b_i bi的更新方式:
- 个性化部分的更新方式不变。初始化时 b u b_u bu和 b i b_i bi全部初始化为0即可。
# _*_ coding:utf-8 _*_
__author__ = "Ricky"
import random
import math
class BiasLFM(object):
def __init__(self, rating_data, F, alpha=0.1, lmbd=0.1, max_iter=500):
'''rating_data是list<(user,list<(position,rate)>)>类型
'''
self.F = F
self.P = dict()
self.Q = dict() # 相当于博客中Q的转置
self.bu = dict()
self.bi = dict()
self.alpha = alpha
self.lmbd = lmbd
self.max_iter = max_iter
self.rating_data = rating_data
self.mu = 0.0
'''随机初始化矩阵P和Q'''
cnt = 0
for user, rates in self.rating_data:
self.P[user] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
self.bu[user] = 0
cnt += len(rates)
for item, rate in rates:
self.mu += rate
if item not in self.Q:
self.Q[item] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
self.bi[item] = 0
self.mu /= cnt
def train(self):
'''随机梯度下降法训练参数P和Q
'''
for step in range(self.max_iter):
for user, rates in self.rating_data:
for item, rui in rates:
hat_rui = self.predict(user, item)
err_ui = rui - hat_rui
# 更新偏置
self.bu[user] += self.alpha * (err_ui - self.lmbd * self.bu[user])
self.bi[item] += self.alpha * (err_ui - self.lmbd * self.bi[item])
for f in range(self.F):
# 更新P、Q
self.P[user][f] += self.alpha * (err_ui * self.Q[item][f] - self.lmbd * self.P[user][f])
self.Q[item][f] += self.alpha * (err_ui * self.P[user][f] - self.lmbd * self.Q[item][f])
self.alpha *= 0.9 # 每次迭代步长要逐步缩小
def predict(self, user, item):
'''预测用户user对物品item的评分
'''
return sum(self.P[user][f] * self.Q[item][f] for f in range(self.F)) + self.bu[user] + self.bi[item] + self.mu
if __name__ == '__main__':
'''用户有A B C,物品有a b c d'''
rating_data = list()
rate_A = [('a', 1.0), ('b', 1.0)]
rating_data.append(('A', rate_A))
rate_B = [('b', 1.0), ('c', 1.0)]
rating_data.append(('B', rate_B))
rate_C = [('c', 1.0), ('d', 1.0)]
rating_data.append(('C', rate_C))
lfm = BiasLFM(rating_data, 2)
lfm.train()
for item in ['a', 'b', 'c', 'd']:
print(item, lfm.predict('A', item)) # 计算用户A对各个物品的喜好程度
4.SVD++
- 由带偏置的LFM继续进化,就可以得到SVD++。
- 值得注意的是,在推荐系统中使用的SVD和线性代数中的SVD并不完全相同。
- 在实际的生产中,用户的评分数据很稀少,也就是说显示反馈比隐式反馈要少很多,那么可以不可以把隐式反馈的因素加入到模型呢?答案是肯定的。
- SVD++就是在模型融入了隐式反馈的因素,索引评分数据可以理解为:评分 = 显示兴趣 + 隐式兴趣 + 偏见。
- 从另一个角度来看,任何用户只要对物品i有过评分,不管评分多少,就已经在一定程度上反映了他对各个隐因子的喜好程度 y i = ( y i 1 , y i 2 , y i 3 … … y i F ) y_i = (y_{i1},y_{i2},y_{i3}……y_{iF}) yi=(yi1,yi2,yi3……yiF), y y y是物品所携带的属性,就如同Q一样,在公式(11)的基础上,SVD++进化为:
- N ( u ) N(u) N(u)是用户u评价过的物品集合。
- 和上面的方式一样,还是基于评分的误差平方和建立目标函数,正则项里加一个 λ ∑ Y j f 2 \lambda \sum Y^2_{jf} λ∑Yjf2,采用随机梯度下降法优化。其他项不变,隐式兴趣部分优化。
- 另外引入了 Y Y Y矩阵,所以也需要计算它的偏导:
- 代码
# coding:utf-8
__author__ = "ricky"
import random
import math
class SVDPP(object):
def __init__(self, rating_data, F, alpha=0.1, lmbd=0.1, max_iter=500):
'''rating_data是list<(user,list<(position,rate)>)>类型
'''
self.F = F
self.P = dict()
self.Q = dict() # 相当于博客中Q的转置
self.Y = dict()
self.bu = dict()
self.bi = dict()
self.alpha = alpha
self.lmbd = lmbd
self.max_iter = max_iter
self.rating_data = rating_data
self.mu = 0.0
'''随机初始化矩阵P、Q、Y'''
cnt = 0
for user, rates in self.rating_data:
self.P[user] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
self.bu[user] = 0
cnt += len(rates)
for item, rate in rates:
self.mu += rate
if item not in self.Q:
self.Q[item] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
if item not in self.Y:
self.Y[item] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
self.bi[item] = 0
self.mu /= cnt
def train(self):
'''随机梯度下降法训练参数P和Q
'''
for step in range(self.max_iter):
for user, rates in self.rating_data:
z = [0.0 for f in range(self.F)]
for item, _ in rates:
for f in range(self.F):
z[f] += self.Y[item][f]
ru = 1.0 / math.sqrt(1.0 * len(rates))
s = [0.0 for f in range(self.F)]
for item, rui in rates:
hat_rui = self.predict(user, item, rates)
err_ui = rui - hat_rui
self.bu[user] += self.alpha * (err_ui - self.lmbd * self.bu[user])
self.bi[item] += self.alpha * (err_ui - self.lmbd * self.bi[item])
for f in range(self.F):
s[f] += self.Q[item][f] * err_ui
self.P[user][f] += self.alpha * (err_ui * self.Q[item][f] - self.lmbd * self.P[user][f])
self.Q[item][f] += self.alpha * (
err_ui * (self.P[user][f] + z[f] * ru) - self.lmbd * self.Q[item][f])
for item, _ in rates:
for f in range(self.F):
self.Y[item][f] += self.alpha * (s[f] * ru - self.lmbd * self.Y[item][f])
self.alpha *= 0.9 # 每次迭代步长要逐步缩小
def predict(self, user, item, ratedItems):
'''预测用户user对物品item的评分
'''
z = [0.0 for f in range(self.F)]
for ri, _ in ratedItems:
for f in range(self.F):
z[f] += self.Y[ri][f]
return sum(
(self.P[user][f] + z[f] / math.sqrt(1.0 * len(ratedItems))) * self.Q[item][f] for f in range(self.F)) + \
self.bu[user] + self.bi[item] + self.mu
if __name__ == '__main__':
'''用户有A B C,物品有a b c d'''
rating_data = list()
rate_A = [('a', 1.0), ('b', 1.0)]
rating_data.append(('A', rate_A))
rate_B = [('b', 1.0), ('c', 1.0)]
rating_data.append(('B', rate_B))
rate_C = [('c', 1.0), ('d', 1.0)]
rating_data.append(('C', rate_C))
lfm = SVDPP(rating_data, 2)
lfm.train()
for item in ['a', 'b', 'c', 'd']:
print(item, lfm.predict('A', item, rate_A) ) # 计算用户A对各个物品的喜好程度
5.ALS算法
- ALS算法是不同于梯度下降法的另一种优化算法,它先随机初始化两个矩阵 X 、 Y X、Y X、Y,然后在固定一个矩阵,再通过最小化等式两边差的平方来更新另一个矩阵,这种更新方式叫做“最小二乘法”,那么交替的固定矩阵,交替的更新矩阵这种方式就被称作“交替最小二乘法”。
- 这里先说一下,在众多的算法中spark为何偏偏钟爱ALS
- 首先,看一下对矩阵 X i X_i Xi的更新方式,注意这里是结果,具体的推导方式在下面给出。
X i = ( Y k ∗ n ∗ Y k ∗ n T + λ ∗ E ) − 1 ∗ Y k ∗ n ∗ r i X_i = (Y_{k*n}*Y_{k*n}^T+\lambda * E)^{-1}*Y_{k*n}*r_i Xi=(Yk∗n∗Yk∗nT+λ∗E)−1∗Yk∗n∗ri - 从上面的式子可以看出, X X X的第 i i i行是 A A A的第 i i i和 Y Y Y的函数,因此可以很容易的分开计算 X X X的每一行,这就为并行计算提供了很大的便捷,也正是因此,Spark这种面向大规模计算的平台选择这个算法。
- 有些人会用embarrassing parallel 来形容这个算法,意思是高度易并行化的——它的每个任务之间没有什么依赖。
- 我们已知评分矩阵是十分稀疏的,SVD在进行矩阵分解时会先把原矩阵进行填充,形成稠密矩阵再进行分解。而ALS的处理方式与SVD不同,这不但大大减小了存储空间,而且spark可以利用这种稀疏性用简单的线性代数计算求解。
- 这几点使得ALS在大规模数据上计算非常快,也解释了为什么spark mllib目前只有ALS这一种算法。
- 首先,看一下对矩阵 X i X_i Xi的更新方式,注意这里是结果,具体的推导方式在下面给出。
【显性反馈和隐性反馈】
- 我们知道,在推荐系统中用户和物品的交互数据分为显示反馈和隐式反馈。在ALS中这两种情况都被考虑了进来,分别可以训练如下两种模型:
//显性反馈模型
val model1 = ALS.train(ratings, rank, numIterations, lambda)
//隐性反馈模型
val model2 = ALS.trainImplicit(ratings, rank, numIterations, lambda, alpha)
- 参数:
rating:评分矩阵rank:隐因子的个数,一般设置为100左右numlterations:迭代次数,调参得到lambada:正则项alpha:置信参数
- 从上面可以看到,隐式模型中多了一个置信参数,这就涉及到ALS中对于隐式反馈模型的处理方式,有的文章称为“加权的正则化矩阵分解”,它的损失函数如下。
- 我们知道,在隐式反馈模型中是没有评分的,所以在式子中 r u i r_{ui} rui被 p u i p_{ui} pui所取代, p u i p_{ui} pui是偏好的表示,取值为1或0,表示用户和物品之间是否有交互,而不是表示评分的高低或者喜好程度。
- 函数中还有一个 c u i c_{ui} cui的项,它用来表示用户偏爱某个商品的置信度,比如交互次数多的权重就会增加,如果我们用 d u i d_{ui} dui来表示交互次数的话,那么就可以把置信度表示成如下公式:
c u i = 1 + α d u i c_{ui}=1 + \alpha d_{ui} cui=1+αdui
- 这里的 α \alpha α就是上面提到的置信参数,是个超参数,需要通过调参来得到。
【使用Spark的ALS模型构建推荐模型】
- 1.为指定用户进行TopN的推荐:
model.recommendProducts(userID, N) - 2.为(用户-物品)对儿进行预测评分,显示反馈或者隐式反馈都可以,是根据两个因子矩阵对应行列相乘得到的数值,可以用来评估系统。既可以传入一对参数,也可以传入以(user,item)对类型的RDD对象作为参数,如:
model.predict(user, item)或者model.predict(RDD[int, int])。 - 3.根据物品推荐相似的物品。这其实不算是一种模型内置的推荐方式,但是ALS可以为我们计算出物品因子矩阵和用户因子矩阵
model.predict(RDD[int, int])model.userFeatures- 这其实是一种降维,让我们可以用更少的维度表示,同时也意味着如果我们要算物品相似度或者用户相似度可以用更少的特征进行计算。进而得到“和这个物品相似的物品”这种类型的推荐。
【ALS算法推导】
- ALS的计算公式:
R m ∗ n ≈ X m ∗ k Y k ∗ n R_{m*n}\approx X_{m*k}Y_{k*n} Rm∗n≈Xm∗kYk∗n
- 损失函数为:
L ( X , Y ) = ∑ u = 0 , i = 0 u = m , i = n ( r u i − x u T y i ) 2 + λ ( ∣ x u ∣ 2 + ∣ y i ∣ 2 ) L(X,Y) = \sum_{u=0,i=0}^{u=m,i=n}(r_{ui}-x_u^Ty_i)^2+\lambda (|x_u|^2+|y_i|^2) L(X,Y)=u=0,i=0∑u=m,i=n(rui−xuTyi)2+λ(∣xu∣2+∣yi∣2) - 参数解释:
- r u i r_{ui} rui属于 R m ∗ n R_{m*n} Rm∗n中的一个元素。
- x u x_{u} xu是 k k k行1列的矩阵, x u T x_{u}^T xuT属于 X m ∗ k X_{m*k} Xm∗k一行元素。
- y i y_{i} yi是 k k k行1列的矩阵,属于 Y k ∗ n Y_{k*n} Yk∗n的一列数据。
- 固定矩阵 Y Y Y, L ( X , Y ) L(X,Y) L(X,Y)对 x u x_u xu求导。
- 因为矩阵运算有性质 ( A T B ) = ( B T A ) T (A^TB) = (B^TA)^T (ATB)=(BTA)T
- ( x u T y i ) (x_u^Ty_i) (xuTyi)是一个数,可以看做是一个方阵;这个不难理解 x u T x_{u}^T xuT的形状是 ( 1 ∗ k ) (1*k) (1∗k),而 y i y_i yi的形状是 ( k ∗ 1 ) (k*1) (k∗1),因此可以有 ( x u T y i ) = ( y i x u T ) = ( y i T x u ) (x_u^Ty_i)=(y_ix_u^T)=(y_i^Tx_u) (xuTyi)=(yixuT)=(yiTxu)。
- 因此可以如下变换:
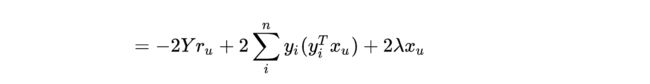
- 因为 y i y_i yi是 ( k ∗ 1 ) (k*1) (k∗1)阶的矩阵,所以 y i ( y i T x u ) y_i(y_i^Tx_u) yi(yiTxu)是符合矩阵乘法结合律的:
( k ∗ 1 ) [ ( 1 ∗ k ) ⋅ ( k ∗ 1 ) ] = ( k ∗ 1 ) ( 1 ∗ k ) ( k ∗ 1 ) (k*1)[(1*k)·(k*1)]=(k*1)(1*k)(k*1) (k∗1)[(1∗k)⋅(k∗1)]=(k∗1)(1∗k)(k∗1)