pytorch【线性回归】【逻辑回归】【softmax回归】

零、前置函数

线性相乘

#线性相乘
def linreg(X, w):
    return torch.mm(X, w)

均方误差损失函数

#均方误差损失函数
#这里的y_hat是我们预测出来的结果，y是我们的正确的结果
def squared_loss(y_hat, y):
#使用y.numel获取到我们y中的元素个数
    num_ = y.numel()
    #reshape(-1,1)的作用就是将我们的函数变成一维的
    #然后我们就将这两个向量对应位置进行相减，然后对新生成的向量的每一个元素都进行求平方的操作
    #然后将这个向量的每一个元素都加起来，得到我们的平方误差和
    sse = torch.sum((y_hat.reshape(-1, 1) - y.reshape(-1, 1)) ** 2)
    #平方误差和除以我们的元素大的个数就是我们的均方误差和 
    return sse / num_

梯度下降函数

def sgd(params, lr):
	#将我们传入的当前位置的w，减去我们的学习率乘以我们梯度
	#我们就得到了我们的一次迭代后我们的新的位置
    params.data -= lr * params.grad 
    #将我们的当前点的梯度清零，节省我们的内存空间，便于我们下一次的计算
    params.grad.zero_()

数据的生成函数

数据的生成函数 小批量数据的随机生成函数

一、线性回归

1.手动实现线性回归

#创建我们的数据集
features, labels = tensorGenReg()
#这个函数在我们上面的数据生成函数的那一篇博文中有
#默认1生成1000行的数据，然后初始的权重是[2,-1,1]，默认是有偏置的
#也就是默认返回一个1000行，2列的数据特征数据
#然后返回一个1000行的标签，也就是1000×2的特征矩阵再乘上一个2×1权重也就是我们上面[2,-1]
#然后再加上我们的偏置，我们就得到了我们的特征
#y=2(x1)-1(x2)+1

# 设置随机数种子
torch.manual_seed(420)    

# 初始化核心参数
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
#也就是说我们全部都训练完的话，我们一共需要完整地遍历三遍全部的数据
num_epochs = 3                                 # 训练过程遍历几次数据
#生成一个三行一列的全0的权重向量，并且允许这个向量进行求导
#这个特征按照我们的传入的数据有多少个特征，我们就生成一个多长的权重矩阵
w = torch.zeros(3, 1, requires_grad = True)    # 随机设置初始权重

# 参与训练的模型方程
net = linreg                                   # 使用回归方程
loss = squared_loss                            # MSE作为损失函数

# 模型训练过程
#我们的模型迭代的次数
for epoch in range(num_epochs):
	#这个data_iter的函数定义在我们上面前置函数的数据的生成模块中有定义
	#传入的三个参数分别是我们的每一个小批量数据的阿晓
	#我们的特征和标签
	#分别取出我们每一次的小批量数据中的特征和标签
    for X, y in data_iter(batch_size, features, labels):
    #用特征乘以权重，然后跟我们的y异同传入我们的误差计算的函数，计算均方误差，
        l = loss(net(X, w), y)
        #将l进行反向传播，也就是由我们的当前的根节点对于我们前面的一个个节点进行求导操作
        l.backward()
        #进行梯度下降，也就是更新我们的权重矩阵
        sgd(w, lr)
    #在我们完成一轮对于全部的数据集的读取之后，我们将我们的特征乘以我们的权重，也就是x*w，然后用跟我们的正确的标签进行比较，计算我们的均方误差，并且打印出来。
    train_l = loss(net(features, w), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l))

2.调库实现线性回归

# 设置随机数种子
torch.manual_seed(420)   

# 创建数据集
features, labels = tensorGenReg()
features = features[:, :-1]                                  # 剔除最后全是1的列
data = TensorDataset(features, labels)                       # 数据封装
#传入我们的数据，然后传入每一个小批量数据集当中的元素个数，然后设置打乱顺序
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)      # 数据加载

1.定义我们线性回归的模型

class LR(nn.Module):
# 定义模型的点线结构
    def __init__(self, in_features=2, out_features=1):       
        super(LR, self).__init__()
		#定义我们的线性模型，默认是传入两个特征，返回一个预测结果
        self.linear = nn.Linear(in_features, out_features)
    
     # 定义模型的正向传播规则
    def forward(self, x):                              
    	#我们的输出就是一对x进行线性回归     
        out = self.linear(x)             
        return out

# 实例化模型
LR_model = LR()

2.定义我们的误差函数

#也就是我们的均方误差
criterion = nn.MSELoss()

3.定义优化方法

#SGD也就是我们的梯度下降的方法，
#传入的两个参数分别是我们模型的全部参数（特征，标签，权重），然后我们的学习率是0.03
optimizer = optim.SGD(LR_model.parameters(), lr = 0.03)

4.模型的训练

#这里定义一个训练函数
#分别传入的是我们的神经网络模型
#我们的损失函数
#我们的优化方法
#我们的每一个小批量的数据的数据个数
#我们的整一个数据集我们一共想完整地遍历几次
def fit(net, criterion, optimizer, batchdata, epochs):
#遍历我们的每一个小批量的数据集
    for epoch in range(epochs):
    #取出每一个小批量数据集当中的特征和标签
        for X, y in batchdata:
        #向前传播，然后得到我们的预测的yhat
		#也就是我们的初始权重乘以我们的特征矩阵的结果
            yhat = net.forward(X)
            #计算我们的均方误差
            loss = criterion(yhat, y)
            #将我们的模型的梯度清空
            optimizer.zero_grad()
            #对我们的模型进行反向传播，也就是一次计算我们的结果对于我们每一个
            #前向结点的导数
            loss.backward()
            #我们的梯度下降进行一次迭代
            optimizer.step() 

5.开始训练

# 设置随机数种子
torch.manual_seed(420)   
#传入我们对应的参数
fit(net = LR_model, 
    criterion = criterion, 
    optimizer = optimizer, 
    batchdata = batchData, 
    epochs = num_epochs)

6.查看模型的参数

# 查看模型参数
list(LR_model.parameters())

7.计算我们模型的当前的均方误差

# 计算MSE
criterion(LR_model(features), labels)

二、逻辑回归

# 设置随机数种子
torch.manual_seed(420)   

# 创建数据集
#这个函数在我们上面的前置函数的数据生成函数的链接中有
# 创建我们的分类数据集，其中分类的类别一共是两类，并且生成偏置项
#然后如果我们不写参数的话，我们的每一个类别都会有500个数据
#然后一共是两类，也就是一共有1000条数据，然后默认的特征是两个
#也就是我们会得到一个1000×2形状的特征和1000×1的标签
features, labels = tensorGenCla(num_class=2, bias=True)

# 可视化展示
plt.scatter(features[:, 0], features[:, 1], c = labels)

1.手动实现逻辑回归

1.激活函数

#这里我们指定sigmid函数作为我们的激活函数，这里的z是w*x，也就是我们预测出来德吉结果
#我们预测出来的结果是一个连续型变量，我们需要将其转换成01型变量。
def sigmoid(z):
    return 1/(1+torch.exp(-z))

2.逻辑回归函数

#也就是将我们逻辑回归的结果进行返回
#也就是调用我们上面1中的函数，然后我们就得到了一个我们的模型对于数据集预测的结果
def logistic(X, w):
    return sigmoid(torch.mm(X, w))

3.辅助函数设定阈值

#辅助函数就是将我们传入的sigma函数之后的结果转换成0-1二分类的结果
#这里我们将sigmid函数大于0.5的标记为1类
#小于等于0.5的标记位第0类
#然后如果我们直接sigma>=p的话我们得到的是一个布尔类型的数组
#我们想要将其变成0,1的话，就需要将其转换成浮点的类型
def cal(sigma, p=0.5):
    return((sigma >= p).float())

4.定义准确率函数

#这个sigma是我们的数据再经过sigmiod函数预测之后的结果，y是我们正确的标签
def accuracy(sigma, y):
    #将两个张量拉平，
    #将我们的sigma根据阈值判别成0,1类型，然后和我们的标签进行比较
    acc_bool = cal(sigma).flatten() == y.flatten()
    #求出平均值，也就是我们的预测正确的个数1（true就是1，然后累加，除以总数）
    #然后得到我们预测正确的百分比
    acc = torch.mean(acc_bool.float())
    return(acc)

5.定义损失函数

#y.numel()是y中一共有多少条数据
def cross_entropy(sigma, y):
#这里我们二分类的损失函数我们定义成交叉熵损失函数
    return(-(1/y.numel())*torch.sum((1-y)*torch.log(1-sigma)+y*torch.log(sigma)))

6.定义优化方法

#这里我们用梯度下降对我们的模型进行优化
#这里的params是我们的权重系数w
def sgd(params, lr):
#这里我们需要单独将data进行迭代，否则我们的函数的可导属性就会丢失
        params.data -= lr * params.grad 
        #将我们的导数清空，便于我们的下一次迭代，并且节省内存
        params.grad.zero_()

7.训练模型

# 设置随机数种子
torch.manual_seed(420)    

# 初始化核心参数
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据
w = torch.ones(3, 1, requires_grad = True)     # 随机设置初始权重

# 参与训练的模型方程
net = logistic                                 # 使用逻辑回归方程
loss = cross_entropy                           # 交叉熵损失函数

# 训练过程
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
    #计算损失函数
        l = loss(net(X, w), y)
        #进行反向传播
        l.backward()
        #对我们的模型进行梯度下降，进行迭代
        sgd(w, lr)
    #计算模型这一轮迭代的准确率
    #也就是将我们的预测出来的准确率跟我们的标签进行对比
    train_acc = accuracy(net(features, w), labels)
    print('epoch %d, accuracy %f' % (epoch + 1, train_acc))

2.调库实现逻辑回归

1.定义核心参数

batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据

2.创建数据集

# 设置随机数种子
torch.manual_seed(420)   

# 创建数据集
features, labels = tensorGenCla(num_class=2)
labels = labels.float()                        # 损失函数要求标签也必须是浮点型
#将我们店的特征和标签进行打包，形成一恶搞对象
data = TensorDataset(features, labels)
#将我们的数据加载到batchData中            
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)

3.定义模型

class logisticR(nn.Module):
    def __init__(self, in_features=2, out_features=1):       # 定义模型的点线结构
        super(logisticR, self).__init__()
        #这里我们定义一层线性回归的模型
        self.linear = nn.Linear(in_features, out_features)
        
    def forward(self, x):                                    
        out = self.linear(x)             
        return out

# 实例化模型
logic_model = logisticR()

4.定义损失函数

#也就是我们的交叉熵损失函数
criterion = nn.BCEWithLogitsLoss()

5.定义优化方法

#这里我们的优化方法就是梯度下降法，然后我们需要传入我们模型的所有数据，然后传入我们的学习率
optimizer = optim.SGD(logic_model.parameters(), lr = lr)

6.定义训练函数

#分别传入我们的神经网络模型，我们的损失函数，我们的优化方法，我们的每一个小批量数据集中元素的个数
#还有我们一共想要在整个完整的数据集上迭代几次
def fit(net, criterion, optimizer, batchdata, epochs):
    for epoch in range(epochs):
        for X, y in batchdata:
        #让我们的模型前向传播，得到我们的一轮的预测结果
            zhat = net.forward(X)
            #用我们第一轮的预测结果计算我们当前的损失
            loss = criterion(zhat, y)
            #将我们的优化方法中的导数进行清空
            #因为我们的梯度是累积的，如果不进行清空的话，梯度就会累计起来
            optimizer.zero_grad()
            #将我们的loss函数进行反向传播
            loss.backward()
            #我们的梯度下降函数进行步进，也就是更新我们的w
            optimizer.step()      

7.开始训练

# 设置随机数种子
torch.manual_seed(420)   
#分别传入我们对应的参数
fit(net = logic_model, 
    criterion = criterion, 
    optimizer = optimizer, 
    batchdata = batchData, 
    epochs = num_epochs)

8.查看训练结果

# 查看模型参数
list(logic_model.parameters())

9.计算交叉熵损失函数

# 计算交叉熵损失
criterion(logic_model(features), labels)

10.计算准确率

def acc_zhat(zhat, y):
    """输入为线性方程计算结果，输出为逻辑回归准确率的函数

    :param zhat：线性方程输出结果 
    :param y: 数据集标签张量
    :return：准确率 
    """
    sigma = sigmoid(zhat)
    return accuracy(sigma, y)

三、softmax回归

# 设置随机数种子
torch.manual_seed(420)   
#这里我们指定我们的均值是6，然后方差是2的正太分布的数据

#然后我们的数据再创建的时候就自动将其调整到我们的0的对称的两边（存在惩罚因子）
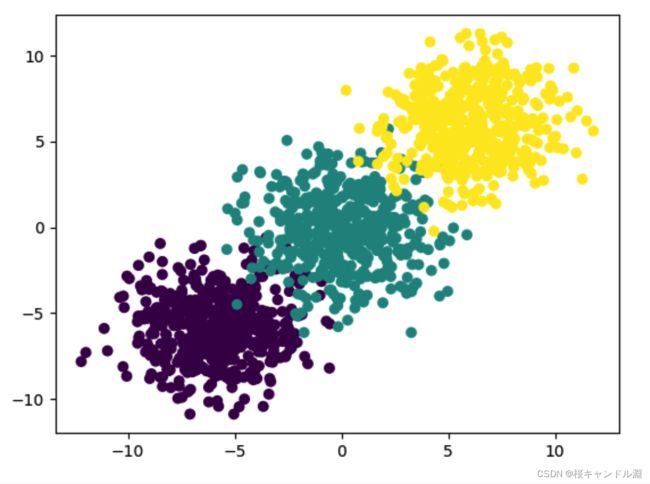
features, labels = tensorGenCla(bias=True, deg_dispersion=[6, 2])
plt.scatter(features[:, 0], features[:, 1], c = labels)

1.手动实现softmax回归

1.softmax函数的定义

def softmax(X, w):
	#将我们预测出来的结果全部变成以e为底的指数
    m = torch.exp(torch.mm(X, w))
    #将我们的上面的m按照行进行相加，然后将我们的性转转换成一列
    sp = torch.sum(m, 1).reshape(-1, 1)
    #用m除以我们的sp，也就是m向量中的每一个元素都会sp中对应行的累加和
    #这样我们就实现了我们的softmax函数
    return m / sp

2.定义交叉熵损失函数

#传入我们预测的结果soft_z和y也就是我们的正确的标签
#这里的soft_z是我们wx进行soft_max函数之后的结果，也就是生成了每一个数据对于不同的标签的概率
#比防说[0.7,0.2,0.1]这样的话就代表着当前这个记录是0类的概率是0.7，是1类的概率是0.2
#是2类的概率是0.1
#
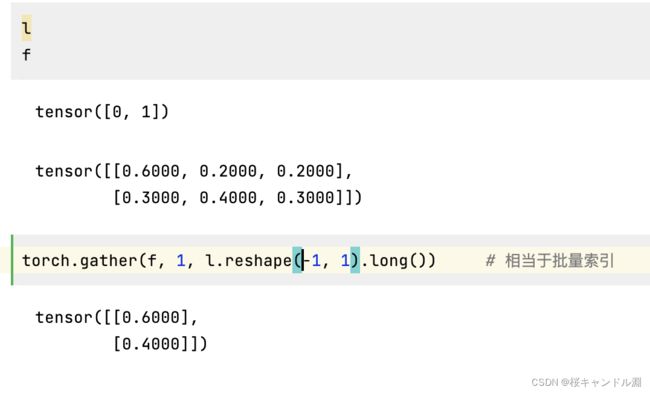
def m_cross_entropy(soft_z, y):
    y = y.long()
    #gather是批量索引的功能，1就是按照行进行索引，y是我们正确的标签
    #也就是我们会索引出我们对于y这个正确的标签预测出来的概率
    prob_real = torch.gather(soft_z, 1, y)
    #y.numel得到y中元素的总个数
    #我们需要将每一个数据进行取对数，然后加和，然后取平均值
    return (-(1/y.numel()) * torch.log(prob_real).sum())

3.定义准确率函数

def m_accuracy(soft_z, y):
#argmax返回当前张量中最大的元素的下标，这里我们也就是我们预测当前样本属于哪一类概率最大的索引
#将这个索引和y进行比较，看看有多少个是标记正确的
#flatten就是将这个数据拉平
    acc_bool = torch.argmax(soft_z, 1).flatten() == y.flatten()
    acc = torch.mean(acc_bool.float())
    return(acc)

4.定义优化函数

#定义梯度下降函数
def sgd(params, lr):
    params.data -= lr * params.grad 
    params.grad.zero_()

5.开始训练我们的模型

# 设置随机数种子
torch.manual_seed(420)  

# 初始化核心参数
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据
w = torch.randn(3, 3, requires_grad = True)    # 随机设置初始权重

# 参与训练的模型方程
net = softmax                                     # 使用回归方程
loss = m_cross_entropy                            # 交叉熵损失函数

train_acc = []

# 模型训练过程
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
    #计算交叉熵损失
        l = loss(net(X, w), y)
        #进行反向传播，反向进行求导
        l.backward()
        #进行梯度下降，更新我们的w
        sgd(w, lr)
    train_acc = m_accuracy(net(features, w), labels)
    print('epoch %d, acc %f' % (epoch + 1, train_acc))

这是我们的w，因为是三分类，所以有三列

2.调库实现softmax回归

1.定义核心参数

batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据

2.创建数据

# 设置随机数种子
torch.manual_seed(420)   

# 创建数据集
features, labels = tensorGenCla(deg_dispersion = [6, 2])
labels = labels.float()                           # 损失函数要求标签也必须是浮点型
data = TensorDataset(features, labels)            
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)

3.定义模型

class softmaxR(nn.Module):
    def __init__(self, in_features=2, out_features=3, bias=False):       
    # 定义模型的点线结构
        super(softmaxR, self).__init__()
        self.linear = nn.Linear(in_features, out_features)
        
    def forward(self, x):                          # 定义模型的正向传播规则
        out = self.linear(x)             
        return out

# 实例化模型和
softmax_model = softmaxR()

3.定义损失函数

#损失函数为交叉熵损失函数
criterion = nn.CrossEntropyLoss()

4.定义我们的优化方法

#我们的优化方法为梯度下降法，然后传入我们模型的所有参数，和学习率
optimizer = optim.SGD(softmax_model.parameters(), lr = lr)

5.定义我们模型的训练函数

#分别传入对应的参数
#我们定义的模型
#我们的损失函数
#我们的优化方法
#我们的每一个小批量数据集中的数据个数
#我们想要在完整的数据集上迭代几次
def fit(net, criterion, optimizer, batchdata, epochs):
    for epoch in range(epochs):
    #分别取出特征和标签
        for X, y in batchdata:
        #向前传播，得出我们的预测结果
            zhat = net.forward(X)
            y = y.flatten().long()       # 损失函数计算要求转化为整数
            #计算损失函数
            loss = criterion(zhat, y)
            #将我们的梯度下降的原有的导数进行清空
            optimizer.zero_grad()
            #将我们的损失函数进行反向传播
            loss.backward()
            #梯度下降，进行迭代
            optimizer.step()

6.训练我们的模型

fit(net = softmax_model, 
    criterion = criterion, 
    optimizer = optimizer, 
    batchdata = batchData, 
    epochs = num_epochs)

7.查看模型的相关参数

# 查看模型参数
print(list(softmax_model.parameters()))

# 计算交叉熵损失
criterion(softmax_model(features), labels.flatten().long())

# 借助F.softmax函数，计算准确率
m_accuracy(F.softmax(softmax_model(features), 1), labels)